الأعداد السالبة
في القسم الخاص بالأعداد الصحية والأعداد الطبيعية توصلنا إلى أن الأعداد الصحيحة تتكون من الأعداد الطبيعية \((0, 1, 2, 3, ....)\) والأعداد السالبة \((-1, -2, -3, ....)\). في هذا القسم سنلقي نظرة أقرب إلى الأعداد السالبة كما سنتعرف على خصائصها.
الأعداد السالبة هي أعداد أقل من الصفر. يُكتب العدد السالب بنفس طريقة العدد الموجب ولكن تُكتب أمامه علامة ناقص ( ''\( -\)'').
في حياتنا اليومية تُقابلنا الأعداد السالبة في سياقات عديدة، بما في ذلك درجات الحرارة الأقل من الصفر (تحت الصفر) على التيرمومترات. على سبيل المثال يمكن القول أن درجة الحرارة الخارجية في يوم بارد هي C°\(-10\), أي 10 درجات تحت الصفر (بدرجة سليزيوس "بالدرجة المئوية").
الأعداد السالبة على خط الأعداد
على خط الأعداد تقع الأعداد السالبة يسار الصفر:
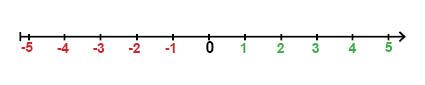
على سبيل المثال المسافة من \(+2\) الى الصفر هي نفس المسافة من \(-2\) الى الصفر. بنفس الطريقة المسافة من أي عدد موجب \(+a\) الى الصفر هي نفس المسافة من العدد المقابل بالسالب \(-a\) الى الصفر. تُسمى الأعداد \(a\) و \(-a\) بالأعداد المتقابلة أو المتضادة، لأنهما يوجدان على بعد مسافتين متساويتين من الصفر، ويوجدان على جانبين مختلفين من الصفر (واحد على الجانب الموجب والثاني على الجانب السالب).
عندما نحسب مع الأعداد السالبة هناك بعض الأشياء يجب وضعها في الاعتبار. عندما نقوم بإضافة شيء ما (جمع)، نتحرك تجاه اليمين على خط الأعداد، وعندما نخصم شيء ما (نطرح) نتحرك تجاه اليسار على خط الأعداد.
إذا كان من الصعب أن نتذكر ذلك، قد يكون من المفيد التفكير في هذا كدرجة الحرارة على التيرمومتر. فإذا كانت درجة الحرارة الخارجية بالسالب (أقل من الصفر) ثم انخفضت (أصبحت أكثر برودة) فسيتم خصم درجات، بالتالي سيزداد عدد درجات الحرارة تحت الصفر لأننا سنتحرك الى الأسفل على المقياس السالب. أما إذا ارتفعت درجة الحرارة (أصبحت أدفأ) فسيتم إضافة درجات، بالتالي سيزداد عدد درجات الحرارة ويصبح الجو أقل برودة ويصبح عدد الدرجات تحت الصفر أقل.
دعونا ننظر إلى مثال على ذلك:
$$-3+4=1$$
لأجراء هذه العملية الحسابية على خط الأعداد سنبدأ عند \(-3\) ونتحرك أربع خطوات (\(+4\)) إلى اليمين على طول خط الأعداد ونتوقف عند \(+1\). أما على التيرمومتر الحراري فهي نفس الشيء كما لو أن درجة الحرارة كانت C°\(-3\) ثم زادت بمقدار C°\(4\), مما يعطينا درجة حرارة جديدة C°\(+1\).
يمكن أن نرى ذلك على خط الأعداد كأننا تحركنا من \(-3\) إلى 1 كما يلي:
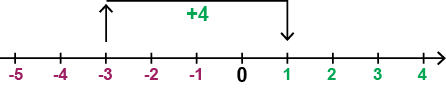
دعونا ننظر إلى مثال آخر:
$$-3-2=-5$$
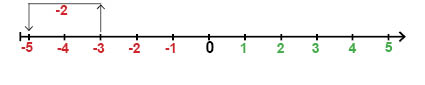
في هذه الحالة سنبدأ عند \(-3\) ثم نطرح الــ 2 بالتحرك خطوتين إلى اليسار على طول خط الأعداد ونتوقف عند \(-5\). أما إذا كانت كدرجة حرارة نريد قياسها فستكون نفس الشيء كما لو أن درجة الحرارة كانت C°\(-3\) ثم زادت بمقدار C°\(2\), مما يعطينا درجة حرارة جديدة C°\(-5\).
على خط الأعداد ستكون كما يلي:
الجمع والطرح
جمع أي عددين يعني أنك تريد معرفة مقدار العددين معا.
العدد السالب هو عدد تحت الصفر (أقل من الصفر) ويُعتبر خصم. فمثلا إذا كان لديك 100 كرونة في البنك وعليك ديون بقيمة 50 كرونة، بالتالي لديك 50 كرونة فقط للاستخدام. بنفس هذا المفهوم يتم جمع الأعداد السالبة:
$$100+(-50)=100-50=50$$
عملية جمع \(-50\) هي نفس عملية طرح 50.
طرح أي عددين يعني أنك تريد معرفة مقدار الفرق بين العددين.
عندما نجتاز الصفر ونطرح عدد أقل منه سيكون الفرق أكبر. على سبيل المثال طائرة على ارتفاع 100 متر فوق سطح البحر ستكون على بعد مسافة 150 متر من قاع البحر الذي عمقه 50 متر أسفل السطح. بالتالي عملية طرح العدد السالب ستكون على النحو التالي:
$$100-(-50)=100+50=150$$
عملية طرح \(-50\) هي نفس عملية جمع 50
إذا كان هناك إشارة سالب أمام الأقواس فيجب تغيير الإشارات لازالة الأقواس, أما في حالة الإشارة الموجبة أمام الأقواس فستظل الأشارات كما هي دون تغيير.
في بعض الأحيان قد يكون لدينا مواقف فيها سنطرح كل ما هو داخل القوسين. فمن ثم علينا أن نتذكر تغيير اشارة كل حد من حدود التعبير داخل القوسين.
وهذا مثال على ذلك:
$$100-(25+25)=100-25-25=50$$
قبل إزالة الأقواس في هذا المثال اخترنا عدم حساب التعبير (25 + 25) أولا، أي تركنا الحدود داخل الأقواس كما هي. لإزالة الأقواس علينا تغيير اشارات جميع الحدود داخل الأقواس. يمكننا أيضا ملاحظة الحصول على نفس النتيجة إذا قمنا بطرح 50 من 100 مباشرة، أي إذا قمنا بحساب التعبير الموجود داخل الأقواس أولا. لتجنب الأخطاء في الحساب، عادة ما يكون من الجيد حساب التعبير داخل الأقواس أولا الى أقصى ما يمكن قبل المواصلة مع باقي التعبير.
وبشكل عام يمكننا تلخيص هذه القواعد الحسابية على النحو التالي:
$$a+(-b)=a-b$$
$$a-(-b)=a+b$$
$$a-(b+c)=a-b-c$$
الضرب والقسمة
حتى في حالة ضرب أو قسمة الأعداد السالبة يجب مراعاة الإشارات.
توجد قاعدتين بسيطتين لعملية الضرب:
القاعدة الأولى: إذا ضربنا عدد سالب فـي عدد موجب سيكون ناتج الضرب عدد سالب:
$$(-3)\cdot 4=-12$$
نعم 3 فـي 4 يساوي 12 ولكن لأن لدينا عدد موجب وعدد سالب فستكون الإجابة سالبة، أي \(-12\).
وتُكتب بشكل رمزي كما يلي:
$$(-a)\cdot b=-ab$$
حيث أن \(a\) و \(b\) عددين موجبين (لذلك \(-a\) عدد سالب).
القاعدة الثانية: إذا ضربنا عددين سالبين فـي بعضهما سيكون ناتج الضرب عدد موجب.
$$(-3)\cdot (-4)=12$$
الآن تم ضرب عددين سالبين فـي بعضهما وفي هذه الحالة تلغي العلامتين السالبتين كل منهما الأخرى، وتكون الإجابة عدد موجب.
وتُكتب بشكل رمزي كما يلي:
$$(-a)\cdot (-b)=ab$$
حيث أن \(a\) و \(b\) عددين موجبين (لذلك \(-a\) و \(-b\) عددين سالبين).
| القاعدة العامة لضرب الأعداد السالبة! | عندما يكون لدينا عدد زوجي من الإشارات السالبة \((2, 4, 6, ...)\) سيكون الناتج بالموجب, أما إذا كان عدد الإشارات السالبة فردي \((1, 3, 5 ...)\) فسيكون الناتج بالسالب. |
بعد وصولنا إلى هذه النقطة يمكننا توضيح كيفية التعامل مع القسمة.
هناك طريقة للتأكد من إجراء عملية القسمة بشكل صحيح وهي ضرب المقام في ناتج القسمة (عملية عكسية). فإذا كان ناتج ضرب المقام فـي ناتج القسمة (المقام×الناتج) مساويا للبسط حينئذ نكون أجرينا عملية القسمة بشكل صحيح. على سبيل المثال قد يكون لدينا
$$\frac{12}{3}=4$$
للتأكد من صحة هذه العملية يمكننا ضرب 3 (المقام) في 4 (ناتج القسمة)، فسنحصل على ناتج الضرب 12 (وهو البسط):
$$3\cdot 4=12$$
الآن ننظر إلى خارج قسمة عددين سالبين
$$\frac{-12}{-3}=?$$
للحصول على ناتج يساوي \(-12\) كما في البسط يجب ضرب \(-3\) فـي 4. أي أن ناتج هذه القسمة هو 4.
$$\frac{-12}{-3}=4$$
وهذا يعني أن ناتج قسمة أي عددين سالبين سيكون عددا موجبا
$$\frac{-a}{-b}=c$$
ماذا سيحدث لخارج القسمة إذا كان لدينا عدد موجب وعدد سالب؟
$$\frac{-12}{3}=?$$
للحصول على ناتج يساوي \(-12\) كما في البسط يجب ضرب 3 فـي \(-4\), أي أن ناتج هذه القسم هو \(-4\).
$$\frac{-12}{3}=-4$$
وهذا يعني أن ناتج قسمة أي عدد سالب علـى عدد موجب سيكون عددا سالبا. وبالمثل ناتج قسمة أي عدد موجب علـى عدد سالب سيكون أيضا عددا سالبا.
$$\\\frac{-a}{b}=-c$$
$$\frac{a}{-b}=-c$$
مُلخص القواعد الحسابية للأعداد السالبة
في نهاية هذا القسم نلخص القواعد الحسابية للأعداد السالبة التي توصلنا إليها:
$$\\a+(-b)=a-b$$
$$a-(-b)=a+b$$
$$ a-(b+c)=a-b-c$$
$$(-a)\cdot b=-ab$$
$$a\cdot (-b)=-ab$$
$$ (-a)\cdot(-b)=ab$$
$$\frac{-a}{b}=-c$$
$$\frac{a}{-b}=-c$$
$$\frac{-a}{-b}=c$$
فيديو الدرس (بالسويدية)
ضرب وقسمة الأعداد الموجبة والسالبة.
وسائل مساعدة
هنا أُستُخدمت الآلة الحاسبة البيانية (الراسمة) (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).
الآلات الحاسبة البيانية من العلامات التجارية الأخرى لديها وظائف مماثلة تقريبا.
