حساب المتجهات
في القسم السابق بدأنا نتعرف على المتجهات وفي هذا القسم سندرس بعض القواعد الحسابية التي يجب تطبيقها عندما نتعامل مع المتجهات.
بما أن المتجه يحتوي على عنصرين هما المقدار والإتجاه فيجب متابعة ومراعاة هاذين العنصرين معا عند حساب المتجهات.
ضرب الكميات القياسية فــي المتجات
كما ناقشنا باختصار في القسم السابق أن الكمية القياسية هي عبارة عن مقدار يتم وصفه بإستخدام الأعداد فقط (بينما المتجهات يتم وصفها بالمقدار والإتجاه معا).
إذا ضربنا متجه ما في كمية قياسية موجبة بالتالي سيحتفظ المتجه باتجاهه السابق ولكن سيكن له مقدار جديد. فمثلا إذا ضربنا المتجه \(\overrightarrow{v}\) فـي الكمية القياسية 3 فسيتضاعف طول المتجه ثلاثة مرات, أي أن مقدار المتجه سيزيد بمقدار العامل 3, كما سنلاحظ في الشكل أدناه.
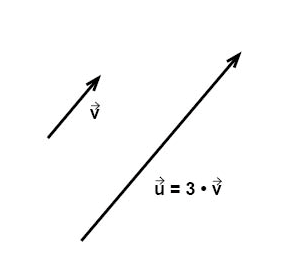
يمكننا على سبيل المثال استخدام مفهوم القوة لتوضيح هذه العملية. القوة لها مقدار (مقياس) وإتجاه (الإتجاه الذي تؤثر فيه القوة). فإذا ضاعفنا قوة ما الى ثلاثة أضعاف فستصبح هذه القوة أكبر بثلاثة مرات ولكن ستحتفظ بنفس الاتجاه كما في السابق، أي أن إتجاهها لا يتغيير.
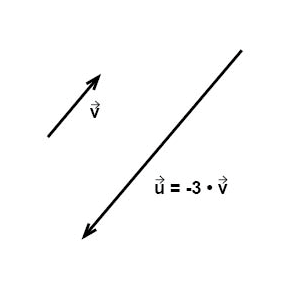
أما إذا ضربنا متجه ما في كمية قياسية سالبة فسيتغيير هذا المتجه مقداراً وإتجاهاً، أي أن هذه العملية ستنتج متجه جديد بمقدار جديد وإتجاه معاكس. فمثلا إذا ضربنا هذا المتجه \((\vec{v})\) فـي \(-3\) ففي هذه الحالة سيصبح طول المتجه ثلاثة أضعاف كما سيكون إتجاهه عكس الإتجاه السابق تماما, ويمكن توضيح ذلك في الشكل أدناه.
جمع المتجهات
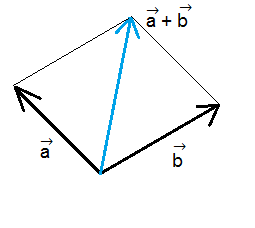
عندما نجمع متجهين مختلفين في الإتجاه سنحصل على متجه آخر بمقدار وإتجاه جديديّن. أما في حالة جمع متجهين لهما نفس الإتجاه فسنحصل على متجه آخر بمقدار جديد ولكن سيكون له نفس الإتجاه. الحدود الناتجة في عملية جمع المتجهات تُسمى بالمركبات بينما يُسمى ناتج (حاصل) مجموعها بالمحصلة. يمكن أن نتصور أن ناتج مجموع متجهين هو عبارة عن قطر متوازي أضلاع تتكون أضلاعه من هاذين المتجهين. في الشكل أدناه المحصلة هي السهم المرسوم باللون الأزرق:
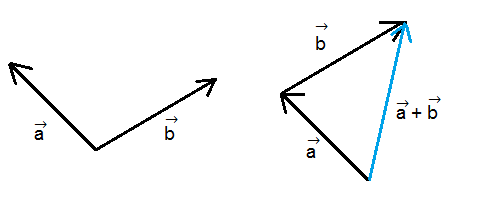
أيضا يمكنك أن تلاحظ عملية التحريك (الإنتقال) المتوازي للمتجه \(\vec b\) كما في الشكل أدناه، بحيث تكون نقطة بدايته مع نقطة نهاية المتجه الآخر (المتجه \(\vec a\) في نفس الشكل). ومن ثم يكون مجموع هاذين المتجهين هو المتجه المرسوم بين نقطة بداية المتجه \(\vec a\) ونقطة نهاية المتجه المنقول \(\vec b\).
طرح المتجهات
في قسم الأعداد السالبة توصلنا إلى أن عملية الطرح هي عبارة عن عملية جمع أعداد سالبة. بنفس المفهوم يمكنك أن تتخيل أن عملية طرح المتجهات هي عبارة عن عملية جمع المتجهات ذات الإتجاه العكسي (أي لها اتجاه معاكس ولكن لها نفس المقدار). ويمكننا كتابتة ذلك على النحو التالي:
$$ \overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+\overrightarrow{(-b)}$$
وذلك لأن عملية ضرب المتجه في الكمية القياسية \(-1\) ستغير إتجاه المتجه فقط ولكن سنحصل على متجه له نفس المقدار تماما، وهو ما يُسمى بالمتجه المعاكس أو المضاد.
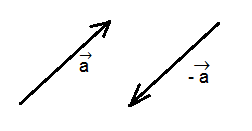
إذا كان لدينا على سبيل المثال متجهين \(\vec a\) و \(\vec b\) كما هو موضح في الشكل أدناه
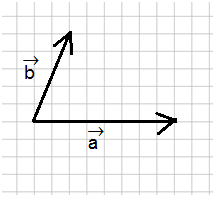
ونريد الحصول على الفرق بين المتجه \(\vec a\) والمتجه \(\vec b\), عندئذ يمكننا تفسير ذلك كما لو كنا نريد مجموع المتجهين \(\vec a\) و \(-\vec b\):
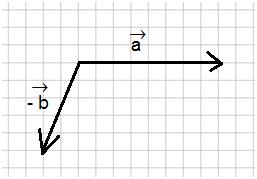
ثم بعد ذلك نجري هذه العملية كأنها عملية جمع متجهات كما رأينا سابقا: نقوم بتحريك أحد المتجهين حركة موازية بحيث تكون نقطة بدايته هي نفس نفطة نهاية المتجه الآخر. ومن ثم سنحصل على الشكل على التالي:
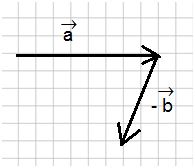
في الشكل التالي المتجه \(\vec c\) المرسوم بين نقطة بداية المتجه \(\vec a\) ونقطة نهاية المتجه \(-\vec b\) هو مجموع المتجهين (المحصلة).
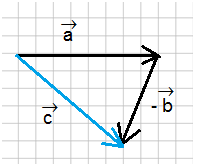
ويمكن التعبير عن المحصلة \(\vec c\) بدلالة المتجهين \(\vec a\) و \(\vec b\) كما يلي:
$$\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})$$
المتجهات في شكل إحداثيات
في قسم المتجهات ذكرنا أن المتجه الذي طوله 1 يُسمى بمتجه الوحدة. كما أشرنا أيضا إلى أنه يمكننا استخدام مثل هذه المتجهات كمتجهات وحدة لها نفس إتجاه محاور نظام إحداثيات.
بإستخدام مثل هذا النوع من متجهات الوحدة يمكننا التعبير عن المتجهات الأخرى.
فإذا نظرنا إلى المتجه \(\vec a\) كمحصلة للمركبتان (المركبة السينية والصادية) \(\vec a_x\) و \(\vec a_ y\) المتوازيتان مع المحور x والمحور y, بالتالي يمكننا التعبير عن إحداثيات المتجه الناتج (المحصلة \(\vec a\)) باستخدام متجهات الوحدة:
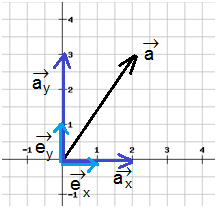
المركبة \(\vec a_x\) يمكن كتابتها في صورة كمية قياسية مضروبة فـي متجه الوحدة \(\vec e_x\), بينما المركبة \(\vec a_y\) يمكن كتابتها في صورة كمية قياسية مضروبة فـي متجه الوحدة \(\vec e_y\), بمعنى أنه يمكن التعبير عن المتجه \(\vec a\) كما يلي:
$$ \\\overrightarrow{a}=\overrightarrow{a_x}+\overrightarrow{a_y}= 2\cdot\overrightarrow{e_{x}}+3\cdot\overrightarrow{e_{y}}=(2,3)$$
نلاحظ أن النقطتان الإحداثيتان (2,3) المستخدمتان لوصف المتجه في شكل إحداثيات هما بالضبط نفس الكميات القياسية المضروبة فـي متجهي الوحدة السيني والصادي للحصول على مركبات المتجه.
إذا أردنا جمع متجهين مكتوبيّن في شكل إحداثيات يمكننا جمع مركبات المتجهين بالترتيب أي جمع المركبة السينية مع المركبة السينية والصادية مع الصادية، ومن ثم نحصل على محصلتهما كما يلي:
$$\\ \begin{align} \overrightarrow{a}+\overrightarrow{b} &=(a_x,\, a_y)\,+\,(b_x,\, b_y)= \\ &=(a_x + b_x,\, a_y + b_y) \end{align} $$
مثلا إذا كان لدينا المتجهين
$$\overrightarrow{a}=(2,3)$$
$$\overrightarrow{b}=(3,1)$$
ونريد معرفة محصلة هاذين المتجهين في صورة إحداثية. بالتالي يمكننا حساب المحصلة وفقا للصيغة أعلاه كما يلي:
$$\overrightarrow{a}+\overrightarrow{b}=(2,3)+(3,1)=(2+3, 3+1)=(5,4)$$
ملخص قواعد حساب المتجهات
يمكننا الآن تلخيص القواعد الحسابية للمتجهات المكتوبة في شكل إحداثيات بصورة عامة كما يلي:
جمع المتجهات
\(\\ \begin{align} \overrightarrow{a}+\overrightarrow{b} &=(a_x,\, a_y)\,+\,(b_x,\, b_y)= \\ &=(a_x + b_x,\, a_y + b_y) \end{align}\)
طرح المتجهات
\(\\ \begin{align} \overrightarrow{a}-\overrightarrow{b} &=(a_x,\, a_y)\,-\,(b_x,\, b_y)= \\ &=(a_x - b_x,\, a_y - b_y) \end{align} \)
الضرب فـي الكميات القياسية
\(s\cdot \overrightarrow{a}=s\cdot (a_x,\, a_y)=(s\cdot a_x,\, s\cdot a_y) \hspace{10cm}\)
حيث أن s هي كمية قياسية.
فيديوهات الدرس (بالسويدية)
فيما يلي سنتعلم كيفية الحساب مع المتجهات.
