حل المتباينات بيانيا

في القسم السابق رأينا كيفية حل المعادلات بيانيا وذلك بصياغة طرفي المعادلة الأيمن والأيسر في شكل دالتين ثم إيجاد نقطة تقاطع هاتين الدالتين. في هذا القسم سندرس كيفية حل المتباينات بيانيا وهي عملية مشابهة لعملية حل المعادلات بيانيا كما سنرى لاحقا.

في قسم المتباينات أوجدنا الحل الجبري لمسألة معينة حيث كانت تكلفة الهاتف فيها لا تتجاوز 400 كرونة في الشهر.

الآن نحل نفس المسألة بيانيا

المتباينة التي سنحلها بيانيا هي \(199 + 0.99x \leq 400\). نبدأ بكتابة هذه المتباينة في شكل دالتين، من كل طرف نحصل على دالة:

$$\left\{\begin{matrix} y_{1}=199+0,99x\\ y_{2}=400\: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \: \end{matrix}\right.$$

ثم بعد ذلك نرسم هاتين الدالتين على نظام إحداثيات، إما يدويا وذلك عن طريق جدولة القيّم ثم نرسم النقاط التي أوجدناها، أو باستخدام الآلات الحاسبة الراسمة:

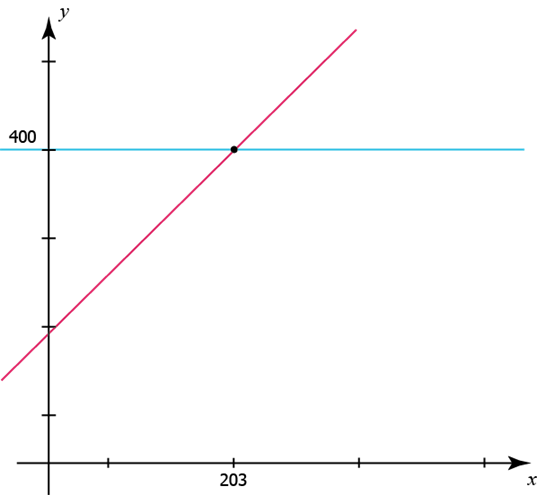
حل هذه المتباينة هو عبارة عن قيّم \(x\) التي يمكن تعويضها في التعبير \(199 + 0.99x\) وتنتج قيمة أقل من أو تساوي 400, ويمكن تفسير ذلك بأن الحل هو قيّم \(x\) التي تقع عند النقطة التي يتقاطع فيها المنحنيين الخاصين بالدالتين أو يسارها. بالتالي حل المتباينة هو ليس بقيمة واحدة لــ \(x\) وإنما هو مجموعة من قيّم \(x\) ويعرف بمدى أو نطاق الحل (بالطبع يمكنك أن تستخدم هذا الهاتف للاتصال لفترة أقلّ‏ من الحد الأقصى للدقائق).

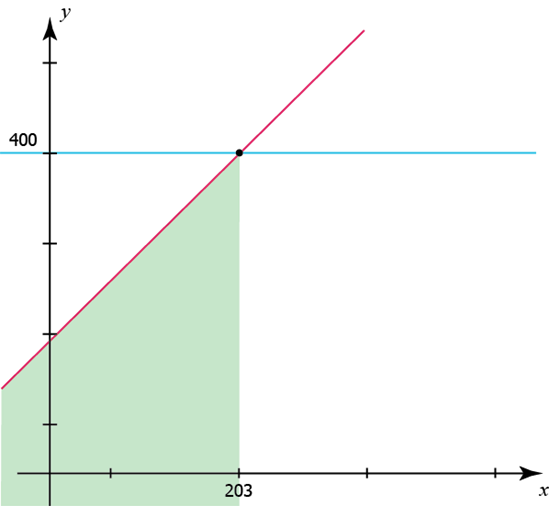
في الشكل أعلاه نلاحظ أن الحل البياني للمتباينة هو أن \(x\) سيكون لها قيمة أقلّ‏ من أو تساوي 203 تقريبا.

فيديوهات الدرس (بالسويدية)

فيما يلي سنشرح كيفية حَل المُتباينات والمعادلات باستخدام الرسوم البيانية (حَل المُتباينات بيانياً).