المتباينات
تُستخدم المعادلات الرياضية لترجمة المسائل الواقعية وعادة ما يكون لدينا طرفين أو تعبيرين رياضيين متساويين بينهما علامة يساوي (=) ولكن لا يمكننا دائما استخدام هذه الطريقة (أي المعادلة الرياضية) لوصف وكتابة بعض المسائل التي لا تستوفي شروط المعادلات، على سبيل المثال نعلم أن 5 نملات أكثر من 4 أفيال ولكن كيف يمكننا التعبير عن ذلك رياضيا. التعبيرات الرياضية أو الأطراف الغير متساوية تُسمى بالمتباينات، وبدلا من استخدام علامة يساوي (=) نستخدم علامة أقل من \((\lt)\) أو أكبر من \((\gt)\).
يمكن كتابة أن 4 أقل من 5 على النحو التالي
$$4<5$$
وبالمثل يمكن كتابة أن 5 أكبر من 4 على النحو التالي
$$5>4$$
هناك قاعدة يجب تذكرها في هذا السياق وهي أن علامة المتباينة يجب أن تكون مفتوحة تجاه القيمة أو الطرف الأكبر. هناك طريقة أخرى لتذكر مفهوم المتباينة وهي ملاحظة أن علامة التباين تبدو كالقمع حيث تكون القيمة الأكبر بجانب فتحة القمع الكبيرة والقيمة الأصغر بجانب فتحة القمع الصغيرة.
القيمة الأقل \(>\) القيمة الأكبر
القيمة الأكبر \(<\) القيمة الأقل
هناك أيضا علامتان يعنيان "أكبر من أو يساوي" و "أصغر من أو يساوي":
$$x\leq 4$$
وتُقرأ "\(x\) أصغر من أو يساوي 4".
$$x\geq 2$$
وتُقرأ "\(x\) أكبر من أو يساوي 2".
هنالك أيضا علامة أخرى تعني "لا يساوي" أو "مختلف عن":
$$x\neq 3$$
وتُقرأ "\(x\) لا تساوي 3" أو "\(x\) مختلفة عن 3".
الحل الجبري
يمكن التعامل مع المتباينات بنفس طريقة المعادلات ويمكننا إيجاد حَل المتباينة بإجراء عمليات حسابية على تعبيرات المتباينة الجبرية. يمكنك إذا أردت المرور على درس حَل المعادلات لتنشيط الذاكرة.
دعونا ننظر إلى مثال على حَل المتباينة
أفرض أن لديك هاتف خلوي وتكلفة الإشتراك الشهرية 199 كرونة بالإضافة لسعر المكالمات، يتضمن عقد الإشتراك أن سعر الدقيقة 99 سنت (جزء من مائة من الكرونة). فإذا كان لا يمكنك دفع أكثر من 400 كرونة في الشهر مقابل المكالمات التلفونية وتريد معرفة عدد الدقائق التي يمكنك إستخدامها للاتصال خلال الشهر.
فإذا رمزنا إلى عدد الدقائق التي يمكنك الاتصال بها شهريا بــ \(x\) يمكننا إنشاء تعبير رياضي للتكلفة الشهرية.
سيكون التعبير الرياضي لتحديد التكلفة الشهرية كما يلي
$$199+0,99x$$
هذا التعبير يجب أن يكون أقل من أو يساوي 400 لأنك لا تستطيع دفع أكثر من 400 كرونة في الشهر. في هذه الحالة يمكننا الحصول على المتباينة التالية
$$199+0,99x\leq 400$$
يمكن التعامل مع المتباينات وحَلها بنفس طريقة المعادلة. نقوم أولا بطرح 199 من الطرفين ونحصل على
$$199+0,99x-199\leq 400-199$$
$$0,99x\leq400-199 $$
$$0,99x\leq 201$$
ثم نقوم بقسمة الطرفين علـى 0,99 للحصول علـى \(x\) وحدها في الطرف الأيسر
$$x\leq \frac{201}{0,99}$$
$$x\leq 203,0303...$$
بمعنى آخر يمكنك بميزانية قدرها 400 كرونة الاتصال لمدة 203 دقيقة شهريا، أي ما يعادل 3 ساعات و 23 دقيقة.
هذا الحل الذي أوجدناه هو في الحقيقة عبارة عن مدى عدد الدقائق وليست بالضرورة أن تكون \(x = 203,0303\) بالضبط لأنه يمكننا الاتصال بإستخدام عدد دقائق أقل من هذا بدون أي تغيير في شروط المتباينة (أي المحافظة على التباين). فإذا أجرينا اتصالات على سبيل المثال لمدة 100 دقيقة \((x = 100)\), يمكننا الحصول على المتباينة التالية
$$199+0,99\cdot 100\leq 400$$
$$199+99\leq 400$$
$$298\leq 400 $$
التباين أعلاه يتعلق بقيمة \(x\), وهو تباين لأن 298 أقل من 400.
ضرب وقسمة المتباينات في الأعداد السالبة
هناك قاعدة مهمة جدا يجب وضعها في الاعتبار عندما نتعامل مع المتباينات: عند ضرب طرفي المتباينة فـي عدد سالب أو قسمة الطرفين علـى عدد سالب يجب عكس علامة التباين إلى الاتجاه الآخر. وذلك لأن عملية الضرب فـي عدد سالب أو القسمة علـى عدد سالب دائما تغير علامة حدود التعبير الرياضي. وهذا من الأشياء التي لا نحتاج للتفكير فيها عند حل المعادلات الرياضية ولكن يجب ألا ننساها في حالة حَل المتباينات الرياضية، خلاف ذلك يتم التعامل مع حدود طرفي المتباينة بنفس طريقة حَل المعادلة.
فيما يلي مثال على كيفية التعامل مع المتباينة
لدينا المتباينة
$$5>4$$
إذا قمنا فقط بضرب طرفي المتباينة فـي \(-1\) سنحصل على ما يلي
$$5>4$$
$$5\cdot (-1)>4\cdot (-1)$$
$$-5>-4$$
وهذا غير مضبوط!
نلاحظ أن هذا ليس صحيح لأن \(-5\) أقل من \(-4\). لذلك عندما نضرب فـي عدد سالب أو نقسم علـى عدد سالب يجب أن نعكس علامة التباين للحفاظ على صحة المتباينة.
$$5>4$$
$$5\cdot (-1)>4\cdot (-1)$$
$$-5{\color{Blue} <}-4$$
فيما يلي مثال على متباينة أخرى
$$70-2x<10$$
$$70-2x-70<10-70$$
$$-2x<-60$$
$$\frac{-2x}{-2}<\frac{-60}{-2}$$
$$x{\color{Blue} >}30$$
لاحظ اننا قمنا بعكس علامة المتباينة وبدلا من أصغر من "\(\lt \)" أصبحت أكبر من "\(\gt\)".
المتباينات على خط الأعداد
يتم تمثيل أي عدد حقيقي على خط الأعداد بوضع علامة معينة في مكان العدد الصحيحة على طول خط الأعداد.
أما إذا أردنا تمثيل متباينة على خط الأعداد فهي ليست قيمة واحدة كالعدد الحقيقي وانما هي عبارة عن مدى (نطاق أو فترة عددية) لمجموعة من القيم على طول خط الأعداد. يمكن تمثيل مثل هذه المجموعة من القيم بإستخدام دوائر مملوءة ودوائر فارغة. إذا كانت الدائرة مملوءة فهذا يعني أن القيمة التي وُضعت عندها الدائرة تنتمي للقيم التي نريد تمثيلها؛ ولكن إذا كانت الدائرة فارغة فهذا يعني أن القيمة التي وُضعت عندها الدائرة لا تنتمي للقيم التي نريد تمثيلها.
فيما يلي أربعة أمثلة على كيفية تتمثيل المتباينات على خط الأعداد
عندما تكون قيمة \(x\) أكبر من \(-2\):
$$x>-2 $$
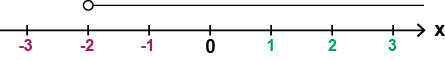
عندما تكون قيمة \(x\) أصغر من 1:
$$x<1$$
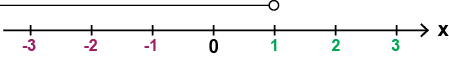
عندما تكون قيمة \(x\) أكبر من أو تساوي 0:
$$x\geq 0$$

عندما تكون قيمة \(x\) أصغر من أو تساوي 0:
$$x\leq 0$$

فيديوهات الدرس (بالسويدية)
فيما يلي سنتحدث عن مفهوم المتباينات و إستخداماتها.
فيما يلي سنشرح كيفية حَل المتباينات.
