مفهوم الدالة
في القسمين السابقين ناقشنا أساسيات نظام الإحداثيات و الرسوم البيانية. في هذا القسم سنتعلم مفهوم الدوال واستخداماته كما سنرى كيفية ربطها بالرسوم البيانية وأنظمة الإحداثيات.
تُستخدم الدالة في وصف العلاقة بين متغيرين أو أكثر.
دعونا نبدأ بمثال على هذا:
عادة ما تعمل الطالبة إيناس في عطلات نهاية الأسبوع وتحصل على أجرها بالساعة وفقا لعدد الساعات الكلي. يمكن إعتبار إجمالي راتب إيناس مقابل عملها كدالة في عدد الساعات التي عملتها.
لنفترض أن أجر إيناس 80 كرونة في الساعة. لوصف إجمالي راتبها يمكننا إنشاء الدالة التالية
$$y=80x$$
حيث \(x\) هو عدد الساعات التي عملتها و \(y\) هو الراتب الذي ينبغي أن تحصل عليه مقابل عملها لمدة \(x\) ساعة.
لكل قيمة من قيّم \(x\) توجد قيمة واحدة لـ \(y\) وتعتمد قيمة \(y\) على قيمة \(x\) - فإذا تغيرت قيمة \(x\) ستتغير قيمة \(y\) أيضا. لذلك تُسمى \(y\) بالمتغير التابع وتُسمى \(x\) بالمتغير المُستقل وتعتمد قيمة المتغير \(y\) على قيمة المتغير \(x\).
الدالة هي عبارة عن علاقة أو قاعدة يمكن تشبيهها بآلة أو ماكينة حيث يمكنك وضع قيمة معينة في إحدى نهايتيها، فلتكن هذه القيمة هي \(x\) مثلا، ومنها تحصل على قيمة أخرى مختلفة من النهاية الأخرى للآلة والتي يمكن أن نطلق عليها \(y\) مثلا. هذه القيمة التي سنحصل عليها تُسمى بقيمة الدالة.
لتوضيح أن \(y\) تعتمد على \(x\) (\(y\) متغير تابع) عادة تكتب الدالة كما يلي
$$y=y(x)$$
وتُقرأ "\(y\) دالة في \(x\)" أو "\(y(x)\)" للتبسيط. يمكن كتابة راتب إيناس في المثال أعلاه على النحو التالي:
$$y(x)=80x$$
الرمز الشائع للدوال التي تعتمد على متغير ما مثل \(x\) هو \(f (x)\).
يمكن وصف الدالة بعدة طرق مختلفة. ما رأيناه أعلاه هو عبارة عن وصف باستخدام صيغة رياضية، كما في حالة راتب إيناس الذي تم وصفه بالدالة التالية.
$$y(x)=80x$$
يمكننا أيضا وصف الدالة لغةً أو حرفياً. بحيث نقول أنه يمكن الحصول على دالة الراتب الكلي بضرب أجر الساعة (80 كرونة) فـي عدد الساعات التي عملتها إيناس.
يمكن أيضا وصف الدوال باستخدام جداول البيانات (جدولة القيّم):
| عدد الساعات: \(x\) | الراتب الكلي: \(y\) |
| 1 | 80 |
| 2 | 160 |
| 3 | 240 |
| 4 | 320 |
| 5 | 400 |
كما يمكن أيضا وصف الدوال برسمها بيانيا على نظام الإحداثيات، على سبيل المثال دالة راتب إيناس يمكن وصفها بالشكل التالي:
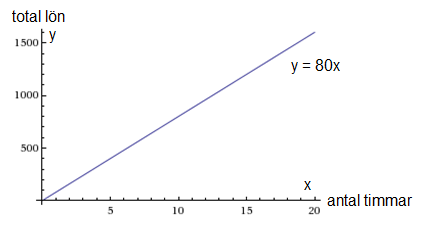
حيث أن total lön على محور \(y\) تعني الراتب الكلي و antal timmar على محور \(x\) تعني عدد الساعات.
لاحظ إختلاف تقسيم المحورين \(x\) و \(y\) على نظام الإحداثيات أعلاه. كما ذكرنا في القسم السابق من المهم جدا اختيار تقسيم أو تدرج مناسب على محاور الإحداثيات، بحيث تظهر العلاقة أو الدالة بشكل واضح. في نظام الإحداثيات أعلاه كل خطوة على طول محور \(x\) تعادل ساعة عمل بينما كل خطوة على محور \(y\) تعادل 100 كرونة.
المجال والمدى
إذا رجعنا إلى دالة راتب إيناس أعلاه نلاحظ أنه يمكنا إدخال قيّم سالبة لـ \(x\) ونحصل على قيمة لــ \(y\) (على سبيل المثال \(x = -1\) ستعطي \(y = -80\)) ولكن ما معنى أن عدد الساعات التي عملتها إيناس عدد سالب؟ ربما نستنتج أن إيناس ستخسر 80 كرونة مقابل كل ساعة لم تعمل فيها، فهذا قد يكون غريبا والى يومنا هذا لا يوجد في سوق العمل مثل هذا النوع من التعامل، وهذا ليس ما نريد وصفه بهذه الدالة.
يمكننا أن نستخلص أن الدالة
$$y=80x$$
يمكن تطبيقها لوصف راتب إيناس كما نريد ولكن لا يمكننا إستخدام قيّم سالبة للمتغير \(x\). بالتالي يجب أن تكون قيّمة \(x\) أكبر من أو تساوي 0. أيضا لا يمكن أن تعمل إيناس عدد من الساعات كما تشاء. بطبيعية الحال لا يزيد معدل ساعات العمل عن 40 ساعة في الأسبوع، أيضا قد لا يسمح رب العمل لإيناس أن تعمل عدد من الساعات كما تريد (علاوة على ذلك, في اليوم 24 ساعة فقط).
وهذا يعني أنه توجد قيّم معينة لـ \(x\) يمكن تطبيقها في الدالة وهي ما تُسمى بالقيّم التي تكون عندها الدالة مُعرفة. وعادة ما تُسمى هذه القيّم لــ \(x\) بمجال الدالة؛ وهذه هي مجموعة قيّم المتغير المُستقل المسموح بها والمتغير المُستقل هو \(x\) في هذه الحالة.
مثلا إذا نظرنا الى فترة اسبوع يمكن أن يكون مجال دالة راتب إيناس كما يلي:
$$0\leq x\leq 40$$
في هذا السياق يمكن تفسير مجال هذه الدالة بأن إيناس يمكنها أن تعمل من صفر إلى 40 ساعة كحد أقصى في الأسبوع.
كل قيمة من قيّم \(x\) المسموح بها تقابلها قيمة معينة لــ \(y\). قيّم \(y\) التي يمكن الحصول عليها تٌسمى بمدى الدالة – مدى الدالة هو مجموعة القيّم التي يمكن الحصول عليها من الدالة.
في المثال أعلاه المجال هو جميع قيّم \(x\) من 0 الى 40 ومجموعة القيّم التي تقابلها هي المدى وهي ما بين 0 (إذا عملت إيناس 0 ساعة أي أنها لم تعمل ستحصل على أجر \((80 × 0 = 0)\) صفر كرونة) الى 3200 (إذا عملت لمدة 40 ساعة ما يعطي أن أجرها سيكون \((80 × 40 = 3200)\) 3200 كرونة).
لذلك يمكننا كتابة المدى على النحو التالي:
$$0\leq y\leq 3200$$
فيديوهات الدرس (بالسويدية)
في هذا الفيديو مقدمة عن مفهوم الدوال وتعريفها وكيفية استخدامها.
فيما يلي سنشرح مفهومي المجال والمدى.
في هذا الفيديو نمر على كيفية وصف الدوال بإستخدام الرسم على نظام الإحداثيات.
