حساب المثلثات
في القسم السابق تعلمنا إحدى النظريات الهامة جدا والمفيدة لتوضيح العلاقة بين أضلاع المثلث القائم الزاوية، وهي ما تُسمى بنظرية فيثاغورس. في هذا القسم سنواصل في دراسة المثلثات القائمة الزاوية، ولكن في هذه المرة سندرس العلاقة بين أطوال أضلاع المثلث وزاوياه الحادة.
تُسمى الأضلاع المختلفة للمثلث القائم الزاوية بأسماء مختلفة وفقا الزاوية التي سندرسها:
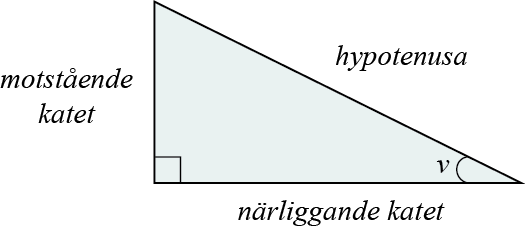
| اللغة السويدية | اللغة العربية |
| motstående katet | الضلع المقابل |
| närliggande katet | الضلع المجاور |
| hypotenusa | الوتر |
في المثلث القائم الزاوية أعلاه سندرس الزاوية \(v\) وسنسمي الأضلاع وفقا لهذه الزاوية. الضلعان اللذان يتقابلان في الزاوية القائمة (°90) هما الضلعين القائمين، والضلع الآخر المقابل للزاوية القائمة هو الوتر. يُسمى الضلع القائم الأقرب للزاوية \(v\) بالضلع المجاور، ويُسمى الضلع القائم المقابل للزاوية \(v\) بالضلع المقابل. وهذه الأسماء سنستخدمها كثيرا في المستقبل.
الدوال المثلثية
جيب الزاوية (sinus)، جيب تمام الزاوية (cosinus) وظل الزاوية (tangens) هي دوال مثلثية تشير إلى النسب المختلفة بين أطوال أضلاع المثلث القائم الزاوية. في بعض كتب الرياضيات باللغة العربية يُرمز لهذه الدوال بــ (جا، جتا و ظا) ولكن هنا سنستخدم الرموز (cos, sin و tan) إختصارا للكلمات أعلاه.
مفهوم هذه الدوال المثلثية هو أن كل زاوية من زوايا المثلث الحادة (\(v\) درجة) لها دائما نسبة معينة بين أضلاع المثلث القائم الزاوية - هذه النسب سنتحصل عليها عند حساب جيب الزاوية \(v\), جيب تمام الزاوية \(v\) وظل الزاوية \(v\), حيث أن لكل دالة من هذه الدوال المثلثية نسبة معينة بين ضلعين مُعينيّن:
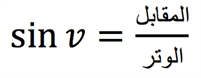
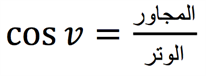
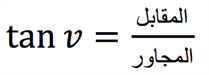
بالتالي لكل زاوية \(v\) توجد قيّم خاصة لكل من الجيب، جيب التمام والظل. كل قيمة من هذه القيّم تشير إلى نسبة بين أطوال ضلعين من أضلاع المثلث - ويعتمد تحديد هذين الضلعين على الدالة المعنية من بين الدوال المثلثية الثلاث وفقا للصيّغ أعلاه.
يمكن استخدام هذه الدوال المثلثية لإيجاد طول الضلع المجهول من بين أضلاع المثلث القائم الزاوية إذا علمنا طول ضلع من الأضلاع الأخرى ومقدار إحدى زاويا المثلث الحادة.
القيّم العكسية للجيب، جيب التمام وظل الزاوية \(v\) هي أيضا مقاييس للزاوية \(v\). يُرمز للقيّم العكسية لجيب الزاوية، جيب التمام والظل بــ ( cos-1 ,sin-1 و tan-1 ) أو (arccos ,arcsin و arctan). أيضا يمكننا استخدام هذه الدوال المثلثية العكسية لإيجاد مقدار إحدى الزاويتين الحادتين للمثلث القائم الزاوية إذا علمنا على الأقل أطوال ضلعين من أضلاع المثلث.
الدوال المثلثية \((\sin, \cos, tan)\) و الدوال المثلثية العكسية \((\arcsin, \arccos, \arctan)\) جميعا مبرمجة في الآلات الحاسبة البيانية. ولكن لاستخدامها بطريقة جيدة، يجب علينا معرفة معاني هذه الدوال وكيفية اجراء العمليات الحسابية للحصول على النتيجة الصحيحة.
احسب الزاوية المجهولة
احسب الزاوية \(v\) الواقعة بين وتر المثلث والضلع الذي طوله 4 وحدات طولية في المثلث القائم الزاوية أدناه:
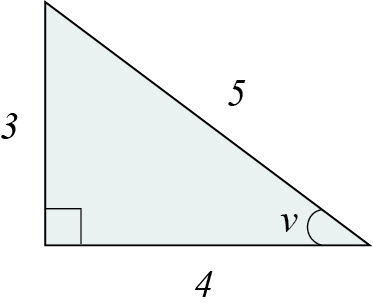
نبدأ بتحديد الزاوية المطلوب في النص: وهي الزاوية الحادة على يمين المثلث. وهذا يعني أن الضلع الذي طوله 4 وحدات طولية هو الضلع المجاور للزاوية \(v\) والضلع الذي طوله 3 وحدات طولية هو الضلع المقابل للزاوية \(v\).
سنحاول أولا حساب الزاوية \(v\) باستخدام دالة جيب التمام. نعوض القيُم المُعطية في صيغة جيب التمام:
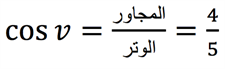
لإيجاد مقدار الزاوية \(v\) سنستخدم دالة جيب التمام العكسية (arccos)
$$v=cos^{-1}\, \left ( \frac{4}{5} \right ) \approx 36,87 ^\circ$$
وتُقرأ الزاوية \(v\) هي الزاوية التي جيب تمامها \(\frac{4}{5}\) وتساوي تقريبا \(36,87 ^\circ\).
الآن بنفس الطريقة سنحاول باستخدام دالة جيب الزاوية. نعوض القيّم المُعطية في صيغة جيب الزاوية:
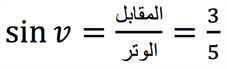
ونحسب مقدار الزاوية \(v\) باستخدام دالة الجيب العكسية (arcsin)
$$v=sin^{-1}\, \left ( \frac{3}{5} \right )\approx 36,87^\circ$$
وتُقرأ الزاوية \(v\) هي الزاوية التي جيبها \(\frac{4}{5}\) وتساوي تقريبا \(36,87 ^\circ\).
وفي الختام سنحسب بنفس الطريقة باستخدام دالة ظل الزاوية:
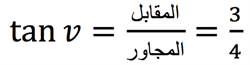
ونحصل على مقدار الزاوية \(v\) باستخدام دالة الظل العكسية (arctan)
$$v=tan^{-1}\,\left ( \frac{3}{4} \right ) \approx 36,87^\circ$$
وتُقرأ الزاوية \(v\) هي الزاوية التي ظلها \(\frac{3}{4}\) وتساوي تقريبا \(36,87 ^\circ\).
كما نلاحظ أننا حصلنا على نفس القيّمة لمقدار الزاوية \(v\) بغض النظر عن الدالة المثلثية المستخدمة.
أحسب أطوال الأضلاع المجهولة
نفترض أن لدينا مثلث قائم الزاوية به زاوية أخرى معلومة مقدارها °48 وطول وتره 5,9 سم، ونريد حساب أطوال الضلعين القائمين.
ينبغي أن نبدأ برسم شكل عام لهذا المثلث حسب المُعطيات أعلاه لكي نحصل على نظرة شاملة على أضلاع وزوايا المثلث، وهذا سيقلل مخاطر إجراء الحسابات بشكل خاطئ:
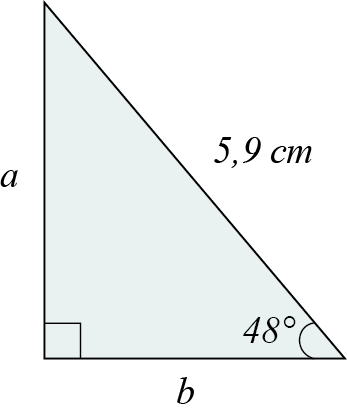
من الشكل نلاحظ أن الضلع b هو الضلع المجاور للزاوية المعلومة، وبما أننا نعلم طول الوتر يمكننا إستخدام دالة جيب التمام لإيجاد طول الضلع b:
$$\cos 48^\circ=\frac{b}{5,9}$$
$$5,9\cdot \cos 48^\circ=\frac{b}{5,9}\cdot 5,9$$
$$5,9\cdot \cos 48^\circ=b$$
$$b\approx3,948\ cm$$
أيضا من الشكل نلاحظ أن الضلع a هو الضلع المقابل للزاوية المعلومة، بالتالي يمكننا إستخدام دالة جيب الزاوية لإيجاد طول الضلع a (يمكننا أيضا استخدام دالة ظل الزاوية لأن طول الضلع المجاور تم حسابه):
$$\sin 48^\circ=\frac{a}{5,9}$$
$$5,9\cdot \sin 48^\circ=\frac{a}{5,9}\cdot 5,9$$
$$5,9\cdot \sin 48^\circ=a$$
$$a\approx4,385$$
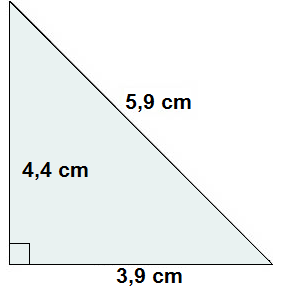
إذن طولا الضلعان المجهولان هما حوالي 4,4 سم (الضلع a) و 3,9 سم (الضلع b).
فيديوهات الدرس (بالسويدية)
هنا سنشرح مفهوم ظل الزاوية والمثلثات المتشابهة.
جيب الزاوية (sinus) وجيب تمامها (cosinus).
هنا سنشرح كيف يمكن إيجاد الزاويه المجهوله بإستخدام الدوال المُثلثيه.
في هذا الفيديو سنشرح كيف يمكننا إيجاد طول ضلع المُثلث بإستخدام الدوال المُثلثيه.
هنا سنتعرف على بعض قيٌم الدوال المُثلثيه.
مقلوب الظل.
مقلوب كل من الجيب وجيب التمام.
وسيلة مساعدة (آلة حاسبة)
في هذا التمرين تم إستخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).
الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريبا.
