معادلات القوى
في الدرس الخاص بالقوى رأينا كيف يمكننا التعبير عن عملية الضرب المتكررة باستخدام القوى، وفي قسم الجذور التربيعية والجذور الأخرى تعلمنا كيف يمكننا استخدام الجذور. في هذا القسم سنتقدم خطوة للأمام ونرى كيف يمكن إستخدام القوى والجذور لحل المسائل الرياضية.
نبدأ بحل مثال من هذا النوع من المسائل:
لنفترض أن لدينا مربع مساحته 144 سم2 (سنتيمتر مربع). فكم سيكون طول ضلع المربع؟
نعلم أن أضلاع المربع متساوية في الطول، ونرمز لطول ضلع المربع بــ \(x\) سنتيمتر.

يمكن حساب مساحة المربع بالصيغة التالية:
Aالمربع = الضلع\(^{2}\)
$$A=x^{2}$$
وهذا ما يعطينا المعادلة التالية
$$144=x^2$$
كما تعلمنا سابقا عن الجذور التربيعية نعلم أن الجذر التربيعي للعدد 144 هو العدد \(x\) الذي حاصل تربيعه 144, وهذا ما يعطينا
$$x=\pm\sqrt{144}=\pm 12$$
وبما أن طول ضلع المربع لا يمكن أن يكون سالبا فإن \(-12\) هي حل غير صحيح في هذه الحالة. بالتالي إذا كان هناك مربع طول ضلعه 12 سم ستكون مساحته 144 سم2.
وهذا يُعتبر مثال على معادلة أسية من الدرجة الثانية وفي هذه الحالة يمكننا أيضا أن نطلق عليها معادلة بسيطة من الدرجة الثانية لأن حلها تم بإجراء خطوة واحدة فقط (إيجاد الجذر).
يمكن أن يكون لدينا معادلات أُسية ذات درجات أعلى، على سبيل المثال معادلات من الدرجة الثالثة، كما سنرى في المثال القادم، حيث نقوم بحل المعادلة بحساب الجذر التكعيبي.
إذا تخيلنا أن لدينا خزان مياه يحتوي على 27 م3 (متر مكعب) من المياه ويأخذ شكل مكعب، فما هو طول ضلع الخزان؟
من درس شبه المكعب نعلم أن أضلاع المكعب متساوية في الطول ويمكننا أن نرمز إلى طول ضلع الخزان بــ \(y\) متر.
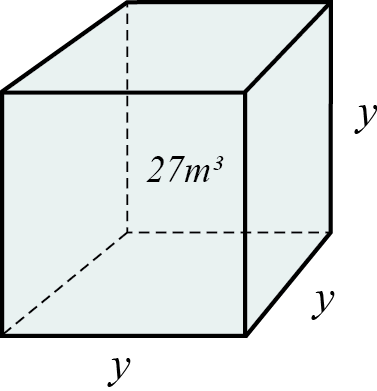
صيغة حجم المكعب هي كما يلي:
Vالمكعب = الضلع\(^3\)
$$V=y^3$$
بالتالي يمكننا الحصول على معادلة الدرجة الثالثة أدناه
$$ 27=y^3$$
يمكننا حل هذه المعادلة بأخذ الجذر التكعيبي للطرفين:
$${27}^{{}^{\frac{1}{3}}}={({y}^{3})}^{{}^{\frac{1}{3}}}$$
$$\sqrt[3]{27}={y}^{{}^{3\cdot \frac{1}{3}}}$$
نلاحظ أن تعبير الطرف الأيمن ينتج \(y\), وبإعادة كتابة المعادلة بحيث نجعل الطرف الأيسر أيمن و الأيمن أيسر سنحصل على:
$$y=\sqrt[3]{27}=3$$
إذن طول ضلع المكعب (الخزان) سيكون 3 متر.
الصورة العامة لمعادلات القوة
المثالان أعلاه يُمثلان حالة خاصة من الصورة العامة لمعادلات القوة وكيفية حلها.
يمكن كتابة معادلة القوة بصورة عامة كما يلي:
$${x}^{n}=a$$
حيث أن \(n\) و \(a\) هما أعداد معلومة و \(x\) متغير.
من القسم الخاص بالقوى تعلمنا كيف يمكننا حساب القوى الأُسية، وهذا ما يمكننا إستخدامه لإيجاد حل الصورة العامة لمعادلات القوى (المعادلات الأُسية).
نرفع طرفي المعادلة للقوة \(\frac{1}{n}\):
$${x}^{n}=a$$
$${({x}^{n})}^{{}^{\frac{1}{n}}}={a}^{{}^{\frac{1}{n}}}$$
$$x={a}^{{}^{\frac{1}{n}}}$$
يمكننا إعادة كتابة الطرف الأيمن كما يلي:
$${a}^{{}^{\frac{1}{n}}}=\sqrt[n]{a}$$
وهو الجذر النوني للعدد \(a\).
بالتالي حل المعادلة هو قيمة \(x\) وهي تساوي الجذر النوني للعدد \(a\).
عِدة جذور
في المثال أعلاه الذي قمنا فيه بحساب مساحة المربع، أخذنا حل المعادلة الموجب فقط (لأن المسافة لا يمكن أن تكون عدد سالب). فإذا أخذنا المثال \(x^2 = 9\), يمكن أن نلاحظ أن
$$x^{2}=9\Rightarrow \sqrt{x^{2}}=\sqrt{9}\Rightarrow x=3$$
ولكن نعلم أيضا أن
$$(-3)\cdot (-3) = 9$$
وهو ما يعني أن \(x^2 = 9\) لها حَليَن:
حل موجب (\(x = 3\)) وحل سالب (\(x = -3\)). وهذا ينطبق على جميع معادلات الدرجات الثانية من هذا النوع أي معادلات الدرجة الثانية البسيطة.
وعادة ما يُكتب أن
$$x=\pm \sqrt{a}$$
وهذان إثنان من حلول معادلات الدرجة الثانية، حيث أن a عدد غير سالب.
القاعدة العامة هي أن عدد جذور أي معادلة يساوي أكبر قوة (أُس) في المعادلة (درجة المعادلة). بمعنى أن
$$x^{3}+cx=a$$
لا تحتوي على أكثر من ثلاثة جذور. والمعادلة
$$x^{4}-x^{2}+x=b$$
لا تحتوي على أكثر من أربعة جذور.
القوى السالبة
حتى الآن ناقشنا القوى الموجبة ولكن ماذا لو كان لدينا قوى سالبة؟
لنفترض أن لدينا المعادلة
$$x^{-3}=8$$
كيف سنتعامل معها؟
من الدرس الخاص بالقوى لدينا قاعدة القوى التالية
$$a^{-b}=\frac{1}{a^{b}}$$
يمكننا استخدام هذه القاعدة لإعادة كتابة هذه المعادلة:
$$ x^{-3}=8 \Leftrightarrow \frac{1}{x^{3}}=8$$
الآن يمكننا استخدام طرق حل المعادلات التي تعلمناها سابقا. نبدأ بضرب المعادلة بالكامل في \(x^3\) للتخلص من الحد \(x^3\) في مقام الطرف الأيسر:
$$\\\frac{1}{x^{3}}\,{\color{Red} \cdot x^3}=8\,{\color{Red} \cdot x^3} \\ \\1=8x^3 $$
في الخطوة التالية نقسم طرفي المعادلة علـى 8 ثم نسحب الجذر الثالث للطرفين ونحصل على قيمة \(x\) كما يلي:
$$\frac{1}{{\color{Red} 8}}=\frac{8x^3}{{\color{Red} 8}} \Rightarrow x^3=\frac{1}{8}$$
$$\sqrt[3]{x^3}=\sqrt[3]{\frac{1}{8}}$$
$$x=\sqrt[3]{\frac{1}{8}}=\frac{1}{2}$$
بالتالي حل المعادلة
$$x^{-3}=8$$
هو
$$x=\frac{1}{2}$$
فيديوهات الدرس (بالسويدية)
فيما يلي سنتعرف على معادلات القوى كما سنشرح كيف يمكن حَلها.
وسيلة مساعدة (آلة حاسبة)
في هذا المثال تم إستخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين بإستخدام الآلة الحاسبة البيانية (Casio FX-9750GII).
الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريباً.
