الدوال الأُسية ودوال القوى

تناولنا في السابق كيفية توضيح ووصف الدوال الخطية من خلال دراسة المعادلة الخطية. في هذا القسم سنتعرف على المعادلات الغير خطية التي تخضع لنوع آخرى من العلاقات.

الدوال الأُسية

ليس من الضروري أن تكون الدالة التي نريد وصفها دالة خطية. مثلا إذا كان لدينا \(50\,000\) كرونة في حساب البنك ونحصل منها على أرباح بمعدل \( 2\, \%\) سنويا، في هذه الحالة سيزيد المبلغ وفقا للجدول التالي:

السنة	رأس المال (بالكرونة)	الأرباح (بالكرونة)	المجموع (بالكرونة)
1	\(50\,000\)	\(50\,000 \cdot 0,02 = 1\,000\)	\(51\,000\)
2	\(51\,000\)	\(51\,000 \cdot 0,02 = 1\,020\)	\(52\,020\)
3	\(52\,020\)	\(52\,020 \cdot 0,02 = 1\,040,40\)	\(53\,060,40\)

سيتغير المبلغ المالي الموجود في الحساب وفقا للأرباح التي ستُضاف اليه كما ستزيد هذه الأرباح كلما زاد المبلغ الموجود في الحساب. وهكذا سيتغير معدل الزيادة بالكرونة السويدية مع مرور الزمن. وبما أن معدل الأرباح سيتغيير وليس ثابت لا يمكننا وصف الرصيد في الحساب باستخدام دالة الخطية.

يمكن مقارنة هذا بالزيادة الخطية (على سبيل المثال إذا حصلنا في السنة على نسبة أرباح \( 2\, \%\) من رأس المال الأصلي):

السنة	رأس المال (بالكرونة)	الأرباح (بالكرونة)	المجموع (بالكرونة)
1	\(50\,000\)	\(50\,000 \cdot 0,02 = 1\,000\)	\(51\,000\)
2	\(51\,000\)	\(50\,000 \cdot 0,02 = 1\,000\)	\(52\,000\)
3	\(52\,000\)	\(50\,000 \cdot 0,02 = 1\,000\)	\(53\,000\)

وفي هذه الحالة (الجدول الأخير) نلاحظ أن الأرباح السنوية (زيادة رأس المال) بالكرونة عبارة عن عدد ثابت خلال الأعوام الثلاثة. المبلغ المالي الموجود في حساب البنك في هذه الحالة يمكن أن نعبر عنه رياضيا كما يلي:

$$y=50\,000+1000x$$

حيث أن \(y\) هو حجم رأس المال و \(x\) هي عدد السنوات بعد وضع المال في الحساب. نلاحظ أن هذه العلاقة هي عبارة عن معادلة خط مستقيم، حيث ان \(k = 1\,000\) و \(m = 50\,000\).

في المقابل الحالة الأولى الغير الخطية هي كما يلي

الأموال بعد \(x\) سنة = رأس المال الأولي \(\cdot \) (عامل التغيير) ^{\(x\) سنة}

هنا المتغير \(x\) يوجد في الأس. معدل الفائدة أو الأرباح وكذلك الدالة في صورة أُسية. وفي هذه الحالة يمكننا كتابة الدالة على النحو التالي:

$$f(x)=50000\cdot 1,02^{x}$$

الآن سنلاحظ الفرق بين رسوم الدوال البيانية على نظام الإحداثيات.

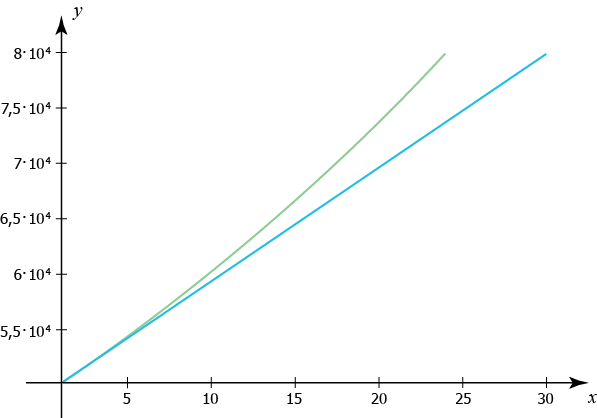
الخط المستقيم الأسفل هو حالة الزيادة الخطية والمنحنى الأعلى هو حالة الزيادة الأُسية. أحد التفسيرات لهاذين الرسمين البيانيين في هذا المثال هو أن الزيادة الأُسية بنسبة \( 2\, \%\) مُرْبحة أكثر من الحصول على مبلغ متكرر بإنتظام بنسبة \( 2\, \%\) من المبلغ الأصلي المُستثمر.

الصورة العامة للدالة الأُسية هي:

$$f(x)=C\cdot a^{x}$$

حيث أن \(C\) و \(a\) ثوابت و \(x\) هي المتغير المُستقل كالعادة. في مثال الدالة الأُسية أعلاه \(C = 50\,000\) و \(a = 1,02\). إذا كان الثابت \(a\) أكبر من 1 ستكون الدالة متزايدة أُسيا وإذا كان \(a\) أصغر من 1 فستكون الدالة متناقصة أُسيا.

دوال القوى

الآن سنناقش نوع آخر من الدوال الغير خطية. أيضا في هذه المرة نبدأ بمثال:

مثلا يمكن وصف السقوط الحر بالدالة

$$s(t)=4,9t^{2}$$

حيث أن \(s\) هي المسافة بالمتر و \(t\) هي الزمن بالثواني.

هذا مثال على دالة قوى. في هذه الحالة يكون المتغير المُستقل هو أساس القوة وليس في الأُس (كما في حالة الدالة الأُسية).

الصورة العامة لدالة القوى هي

$$f(x)=C\cdot x^{n}$$

حيث أن \(C\) و \(n\) ثوابت و \(x\) هي المتغير المُستقل.

إذا كان \(n = 0\) أو \(n = 1\) فستكون الدالة دالة خطية وإذا رسمناها سنحصل على خط مستقيم. وبعبارة آخرى، فإن الدالة الخطية هي حالة خاصة من دوال القوى. إذا لم تكن الدالة دالة خطية فسيكون لها شكل منحنى عند رسمها – مثل هذه المنحنيات يمكن أن يتغيّر شكلها بصورة كبيرة.

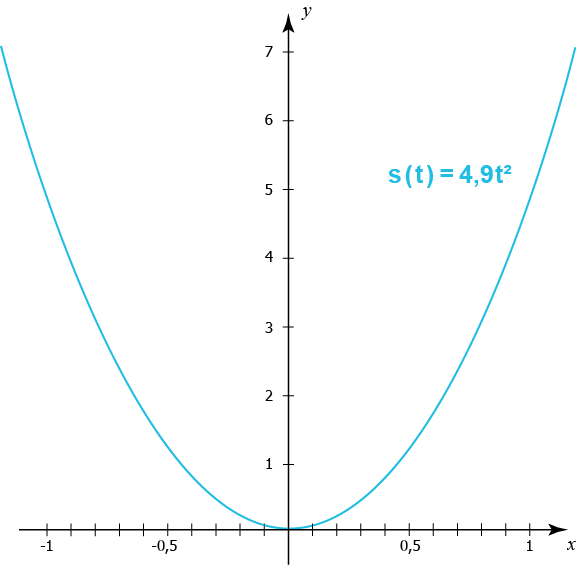
الشكل أعلاه عبارة عن رسم توضحي لدالة السقوط الحر على نظام الإحداثيات. في هذه الحالة لدينا دالة قوى حيث أن قيّم الثوابت هي \(C = 4.9\) و \(n = 2\).

إذا تم تحديد قيمة أي من المتغيرات \(t\) أو \(s\) سنحصل على معادلة قوى كما درسناها في السابق.

---

فيديوهات الدرس (بالسويدية)

فيما يلي سنستعرض الدوال الأُسية و دوال القوى.

في هذا الفيديو سنحسب عدد البكتريا (الجراثيم) بإستخدام مفهوم الدالة الأُسية.

العامل المساعد (آلة حاسبة)

هنا تم إستخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).

الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تغريبا.