المحيط والمساحة

في هذا الباب سنتعلم العلاقات الرياضية لعدد من الأشكال الهندسية المختلفة. وسنبدأ في هذا القسم بإلقاء نظرة قريبة على كيفية إيجاد المحيط والمساحة للأشكال الهندسية الشائعة كالمستطيلات، المثلثات والدوائر.

المحيط

محيط الشكل هو مجموع أطوال الخطوط و/أو المنحنيات التي تُحدد أو تُحيط الشكل.

الأشكال الرباعية تحتوي دائما على أربعة أضلاع، وبجمع أطوال هذه الأضلاع الأربعة سنحصل على محيط الشكل الرباعي. فيما يلي بعض الأشكال الرباعية الأكثر شيوعا.

متوازي الأضلاع

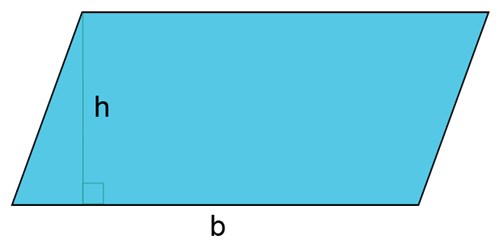
يحتوي متوازي الأضلاع على أربعة أضلاع وكل ضلعين متقابلين متوازيين.

المستطيل

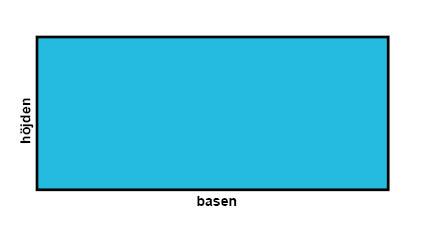
المستطيل هو حالة خاصة لمتوازي الأضلاع، حيث أن لديه زوايا قائمة فقط. مما يعني أن جميع المستطيلات هي أيضا عبارة عن متوازي أضلاع.

المربع

والمربع هو حالة خاصة للمستطيل، حيث أن جميع أضلاعه متساوية في الطول. مما يعني أن جميع المربعات هي عبارة عن مستطيلات، وبما أن جميع المستطيلات عبارة عن متوازي أضلاع، فهذا يعني أيضا أن جميع المربعات عبارة عن متوازي أضلاع.

المثلث

يحتوي المثلث دائما على ثلاثة أضلاع وبنفس المفهوم كما في حالة الأشكال الرباعية فإن محيط المثلث هو مجموع أطوال أضلاعه الثلاثة.

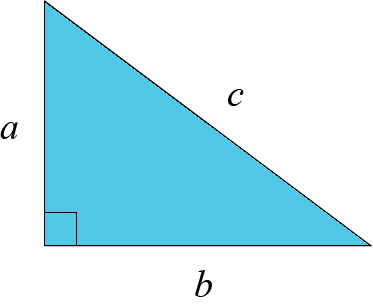
الدائرة

حساب محيط الشكل الرباعي أو المثلث أمر بسيط إذا علمنا أطوال أضلاع كل منهما. أما حساب محيط الدائرة أمر أكثر تعقيدا.

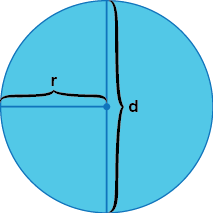
حاصل قسمة محيط أي دائرة على قطرها دائما يساوي نفس النسبة، بغض النظر عن الدائرة التي نختارها كبيرة كانت أو صغيرة. النسبة هي دائما نفس النسبة، وهي تقريبا 3,14. هذا العدد يُسمى باي (pi) ويُشار إليه بالرمز \(\pi\). بالتالي يمكن تعريف باي (pi) كما يلي:

$$\Large{\pi}=\frac{\Large{\textbf{المُحيط}}}{\Large{\textbf{القُطر}}}$$

إذا رمزنا إلى نصف قطر الدائرة بالرمز r, فمن ثم يمكن إعادة كتابة هذه العلاقة على النحو التالي

المحيط = القُطر \(2\cdot \pi \cdot r = \pi \cdot \)

بالتالي يعتمد محيط الدائرة على نصف قطر الدائرة \(r\) فقط ( \(2\pi\) هي قيمة ثابتة).

المساحة

المساحة هي مقياس مقدار المساحة السطحية ويتم حسابها بناءاً شكلها. فيما يلي بعض الأشكال الأكثر شيوعا وكيفية حساب مساحتها.

المربع, المستطيل و متوازي الأضلاع

مساحة كل من المربع، المستطيل أو متوازي الأضلاع تخضع جميعها لصيغة واحدة وهي:

المساحة = القاعدة \(\cdot\) الإرتفاع

$$Arean=basen\cdot höjden$$

ويمكن كتابتها كما يلي

$$A=b\cdot h$$

بالنسبة للمربع والمستطيل تُشكل القاعدة b أحد الأضلاع، بينما يُشكل الارتفاع h أحد الأضلاع المجاورة للقاعدة. عادة ما يتم اختيار الضلع الأفقي الأسفل من المربع أو المستطيل لتمثيل القاعدة بينما يكون الارتفاع هو أحد الأضلاع الرأسية للشكل. بالنسبة لمتوازي الأضلاع تكون القاعدة b هي أحد أضلاع الشكل بينما ارتفاعه هو المسافة المتعامدة بين القاعدة والضلع المقابل (الموازي) لها.

المثلث

يأخذ المثلث القائم الزاوية شكل المستطيل المقسوم قُطريا.

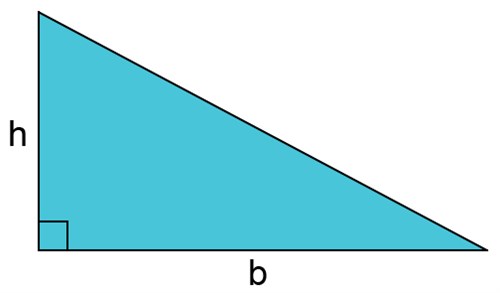
فإذا وضعنا هذا في الإعتبار فليس هنالك غرابة أن تكون مساحة المثلث هي نصف مساحة المستطيل الذي له نفس القاعدة والارتفاع.

بصورة عامة صيغة مساحة المثلث هي كما يلي:

$$A_{\bigtriangleup}=\frac{b\cdot h}{2}$$

صيغة مساحة المثلث الغير قائم الزاوية هي نفس الصيغة. بحيث يتم تحديد الارتفاع بالمسافة العمودية (مع القاعدة) بين رأس المثلث وقاعدته كما في الشكل التالي: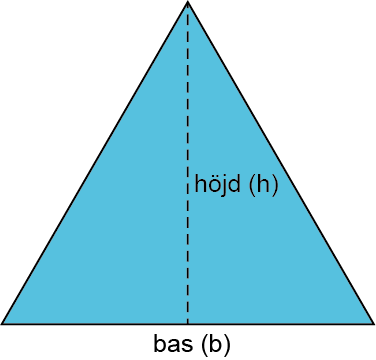

الدائرة

يتم حساب مساحة الدائرة وفقا للصيغة:

$$A_{\bigcirc}=\pi \cdot r^{2}$$

مرة أخرى نشير هنا إلى نصف قطر الدائرة بالرمز r. وكما رأينا في الصيغة أعلاه تعتمد مساحة الدائرة على نصف قطر الدائرة فقط (\(\pi\) هي قيمة ثابتة).

بعض الأشياء التي يجب التفكير فيها عند حساب المساحة

يجب دائما قياس مساحة السطح بالوحدات المربعة. الوحدة المربعة يمكن أن تكون على سبيل المثال متر مربع (مساحة مربع طول ضلعه واحد متر هي متر مربع ويُرمز لها بــ م\(^{2}\)) أو سنتيمتر مربع (مساحة مربع طول ضلعه واحد سنتيمتر هي سنتيمتر مربع ويُرمز لها بــ سم\(^{2}\).

بما أن المساحة هي مقياس مقدار سطحي فمن الممكن قطع وتحريك أجزاء الشكل لإنشاء شكل آخر وذلك لتسهيل حساب المساحة. مع مراعاة الحفاظ على شكل السطح الأصلي لا يتأثر بإعادة ترتيب أجزاء الشكل فسيكون المقدار هو نفسه.

أيضا عند عملية حساب المساحة من المهم وضع وحدات المساحة في الاعتبار على سبيل المثال, 1 م\(^{2}\) لا يساوي 10 دسم\(^{2}\) أو 100 سم\(^{2}\). 1 م\(^{2}\) هو عبارة عن 100 دسم\(^{2}\) أو 10000 سم\(^{2}\), وذلك لأن:

1 م\(^{2}\)= 1 م × 1 م = 10 ديسيمتر × 10 ديسيمتر = 100 دسم\(^{2}\)

بنفس الطريقة

1 م\(^{2}\) = 1 م × 1 م = 100 سم × 100 سم = 10000 سم\(^{2}\)

فيديوهات الدرس (بالسويدية)

مفهوم المُضلع.

كيف يمكن حساب مُحيط ومساحة كل من المثلث والمُربع.

كيف يمكن حساب مُحيط ومساحة كل من متوازي الأضلاع والمستطيل.

كيفية حساب مُحيط ومساحة الدائرة.

كيفية حساب مُحيط ومساحة القطاع الدائري.

وسيلة مساعدة

هنا تم استخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).

الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريبا.