المتجهات
قد تختلف السرعات (على سبيل المثال السيارة تسير بسرعات مختلفة) ويكون لها اتجاهات مختلفة (يمين، يسار، للأمام، للخلف، للأعلى، للأسفل، إلخ...). السرعة هي مثال على الكميات التي يمكن وصفها بالمتجات.
المتجهات
المتجه هو عبارة عن كمية لها مقدار (مقياس/حجم) واتجاه، بمعنى أن المتجه هو كمية متجهة، وليس كالكميات القياسية وهي كميات لها مقدار فقط وليس لها إتجاه (على سبيل المثال الحجم أو درجة الحرارة).
ومن الأمثلة الأخرى على الكميات التي يمكن وصفها بالمتجهات القوة والتسارع أو العجلة كما تُسمى في بعض البلدان العربية. إستخدام المتجهات وقواعدها الحسابية أمر مفيد في تسهيل إجراء العمليات الحسابية، على سبيل الثال عندما يكون لدينا عدد من القوى (القوات) الكبيرة المختلفة تعمل (تُؤَثّر) على شيء ما من اتجاهات مختلفة ونريد معرفة التأثير الكلي لهذه القوى.
عادة ما يُرمز إلى المتجهات بحروف فوقها سهم لتوضيح أن هذه الكمية لها مقدار واتجاه, فمثلا يمكننا استخدام حروف نقطتي البداية والنهاية (\(\vec{AB}\)) أو أي حرف آخر مثل (\(\vec{v}\)) وفيما يلي مثال على ذلك:
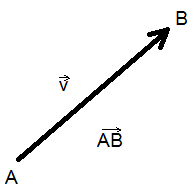
حيث أن المتجه \(\overrightarrow{v}=\overrightarrow{AB} \)
لتوضيح مفهوم هذا المتجه في الشكل أعلاه نقول أن هذا المتجه له نقطة بداية (A) ونقطة نهاية (B), واتجاه موضح بسهم مرسوم بين هاتين النقطتين.
طول السهم يمثل مقدار أو مقياس المتجه بينما يشير السهم إلى اتجاه المتجه. المتجهات التي لها نفس الطول ونفس الاتجاه متشابهة.
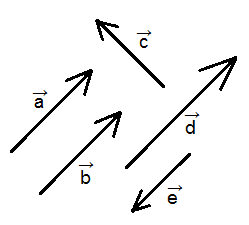
في الشكل أعلاه المتجهان \(\overrightarrow{a} \) و \(\overrightarrow{b} \) متشابهان. ولكن على الرغم من أنهما متماثلان يجب إستخدام المقدار والإتجاه معا لتحديد أن هاذان المتجهان متساويان.
المتجهات المتوازية
نقول أن المتجهان متوازيان عندما يكون لهما نفس الإتجاه أو عندما يكونان متضادان في الإتجاه.

فمثلا في الشكل أعلاه المتجهات \(\overrightarrow{a}\), \(\overrightarrow{b}\), \(\overrightarrow{d}\) و \( \overrightarrow{e}\) متجهات متوازية، حيث أن \(\overrightarrow{a}\), \(\overrightarrow{b}\) و \(\overrightarrow{d}\) لها نفس الإتجاه بينما \(\overrightarrow{e} \) له الإتجاه العكسي.
مقدار/مقياس المتجه
يُسمى طول المتجه بمقدار أو مقياس المتجه، كما يُسمى أيضا بالقيمة المطلقة للمتجه ويُرمز له بالرمز \(\left | \vec{v} \right | \).
يتم الحصول على طو المتجه باستخدام نظرية فيثاغورس.
لننظر إلى مثال على كيفية حساب طول المتجه:
نريد حساب طول المتجه \(\vec v\) المرسوم في نظام الإحداثيات أدناه:
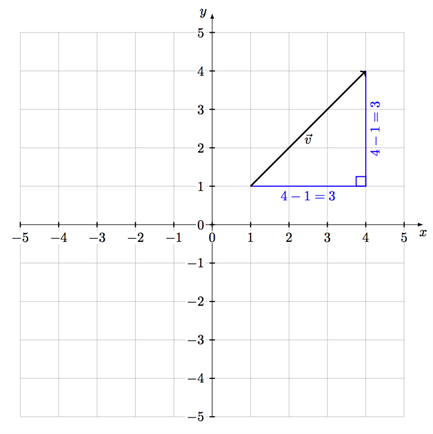
من بداية ونهاية هذا المتجه يمكن إنشاء مثلث قائم الزاوية على إمتداد محوري x و y كما في الشكل أعلاه، الضلعين القائمين لهذا المثلث يُمثلان طول المتجه على إمتداد المحورين x و y. لحساب طول هذا المتجه علينا أولا أن نتعرف على أطوال الضلعين القائمين في المثلث القائم الزاوية أعلاه.
من الشكل نلاحظ أن طول كل من الضلعين القائمين هو \((4-1 = 3)\) وحدات طولية, ويمكن إستخدام هاذين الطولين في نظرية فيثاغورس للحصول على طول الوتر (وهو طول المتجه):
$$\left | \vec{v} \right |\;=\;\sqrt{\left ( 4\;-1 \right )^{2}+\left ( 4\;-\;1 \right )^{2}}=\sqrt{3^{2}\;+\;3^{2}}=\sqrt{18}\approx 4,24$$
التحريك المتوازي للمتجهات
في نظام الإحداثيات يمكن تحريك المتجه حركة متوازية بدون تغيير طوله أو اتجاهه. وهذا ما يُسمى بالإنتقال المتوازي للمتجه، ويمكن استخدامه لتحريك المتجهات إلى نقطة الأصل.
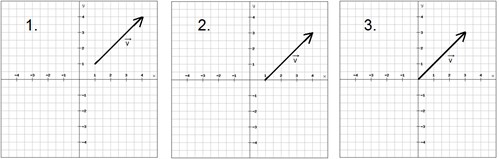
وضْع نقطة بداية المتجه عند نقطة الأصل عملية مفيدة في تمثيل المتجه بدلالة إحداثيات نقطة نهايته. بمعنى أنه يمكننا تمثيل المتجه مقدارا وإتجاها باستخدام نقطة إحداثية واحدة فقط.
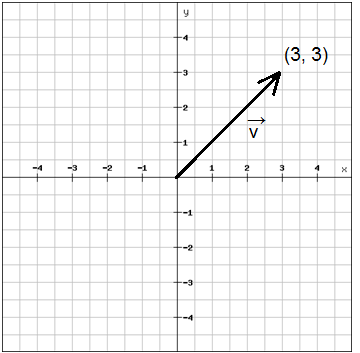
بالتالي يمكننا وصف المتجه أعلاه كما يلي
$$\overrightarrow{v}=\left ( 3,\;3 \right )$$
متجهات الوحدة
المتجه الذي طوله 1 يُسمى بمتجه الوحدة. متجهات الوحدة على إمتداد المحاور في نظام الإحداثيات مفيدة جدا, لأنه يمكننا استخدامها للتعبير عن متجهات أخرى, كما سنرى في القسم القادم.
فيديوهات الدرس (بالسويدية)
في هذا الفيديو سنشرح مفهوم المُتجه.
هنا سنشرح كيفية حِساب طول المُتجه.
في هذا الفيديو نتعرف على كيفية حساب طول المتجه.
