نظام الإحداثيات (المحاور)
سابقا في مرحلة الأساس وتحديدا في العام الدراسي التاسع درسنا نظام الإحداثيات وتعلمنا كيف يمكن استخدامها لوصف وعرض النقاط الإحداثية التي تحتوي على قيمة من \(x\) وقيمة من \(y\) أي في صورة (\(x,y\)). في هذا القسم سنكرر هذه المفاهيم للإستفادة منها لاحقا في كيفية استخدام أنظمة الإحداثيات في سياقات مختلفة.
نظام الإحداثيات هو عبارة عن خط أعداد ثنائي الأبعاد، أي خطان عدديان يُعرفان بمحوري الإحداثيات ويلتقيان مع بعضهما البعض بزاويا قائمة. يُسمى المحور الإحداثي الأفقي بمحور \(x\) ويُسمى المحور الإحداثي الرأسي بمحور \(y\).
يتقاطع محور \(x\) مع محور \(y\) عند نقطتيهما 0, أي عندما تكون قيمة كل من \(x\) و \(y\)مساوية للصفر: \(x = 0\) و \(y = 0\) وتُعرف هذه النقطة التي يتقاطعان فيها بنقطة الأصل (origo).
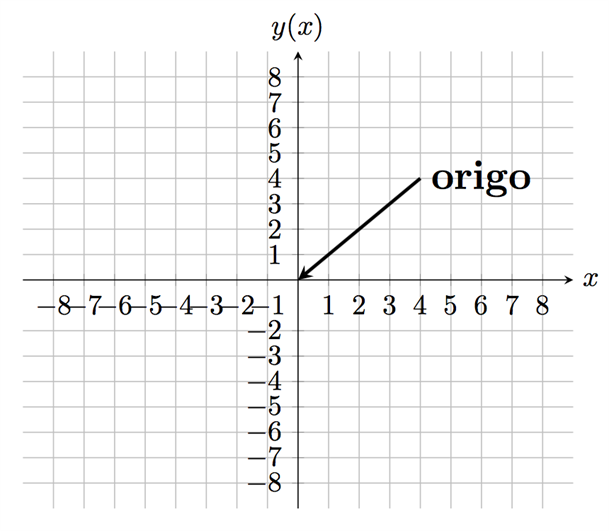
إذا تم تحديد نقطةٍ ما في أي مكان على نظام الإحداثيات يمكننا قراءة قيمة النقطة من المحورين وذلك برسم خطوط مستقيمة من النقطة عمودياً على المحورين.
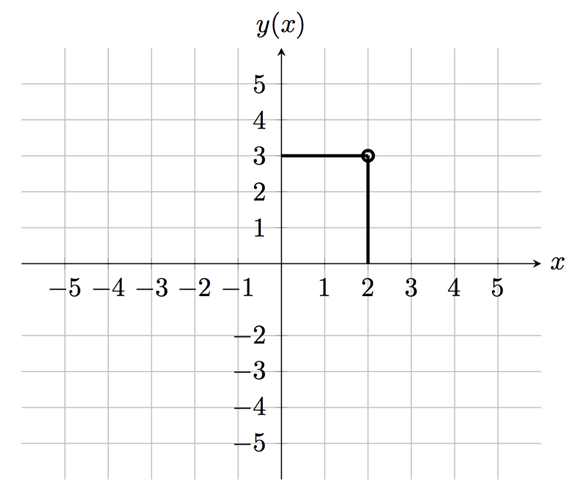
في نظام الإحداثيات أعلاه، تم تحديد نقطة، وكان إحداثي \(x\) هو 2 وإحداثي \(y\) هو 3. عادة ما تُكتب النقطة الإحداثية بين قوسين \((x, y)\), بحيث يتم وضع قيمة \(x\) أولا وقيمة \(y\) ثانيا. وعادة ما يتم فصلهما داخل القوسين بفاصلة عادية أو فاصلة منقوطة. النقطة المحددة في نظام الإحداثيات أعلاه تقرأ \((2, 3)\). وكما ذكرنا أعلاه أن قيّم نقطة الأصل هي \(x = 0\) و \(y = 0\) ويمكن كتابة إحداثيات نقظة الأصل بنفس الطريقة \((0, 0)\).
أحيانا يتم تقسيم نظام الإحداثيات إلى أربع أرباع كما هو موضح في الشكل أدناه:

فيما يلي الفرق بين هذه الأرباع: في الربع الأول قيّم كل من \(x\) و \(y\) موجبة، في الربع الثاني قيمة \(x\) سالبة وقيمة \(y\) موجبة، في الربع الثالث قيّم كل من \(x\) و \(y\) سالبة وفي الربع الرابع قيمة \(x\) موجبة وقيمة \(y\) سالبة.
إذا كان لديك مسألة رياضية تنص على أنه يجب إيجاد الحل الموجود في الربع الأول مثلاً، في هذه الحالة هو الحل الوحيد المسموح به وهذا يعني أن قيمة كل من \(x\) و \(y\) موجبة.
فيديوهات الدرس (بالسويدية)
فيما يلي سنتعرف على نظام الإحداثيات و كيفية عملها وإستخدامها.
مثال آخر على كيفية عمل نظام الإحداثيات.
