تفسير الرسوم البيانية
كما رأينا سابقا في قسم الإحصاء بعض الأمثلة عن عملية جمع البيانات والمعلومات وتحليلها ومن ثم تقديمها بطريقة تجعل من السهل إستيعاب هذه المعلومات.
استخدام الرسوم البيانية هي الطريقة الشايعة لتوضيح المعلومات الإحصائية. هناك عدة أنواع مختلفة من الرسوم البيانية. يمكن أستعراض وتقديم نفس المعلومات على أغلب أنواع هذه الرسوم البيانية ولكن ستظهر بأشكال مختلفة اختلاف بسيط حسب نوع الرسم المستخدم. يتم إختيار نوع الرسم البياني بناءا على المعلومات التي نريد عرضها.
ومن الأنواع الأكثر شيوعا للرسوم البيانية هي الرسم البياني الدائري، الرسم البياني الخطي، الرسم البياني الشريطي، الرسم البياني العمودي، والمدرج التكراري (histogram).
الرسم البياني الدائري
الرسم البياني التالي هو عبارة عن رسم بياني دائري يوضح إجابات \(1\,000\) شخص على أحد الاستطلاعات.
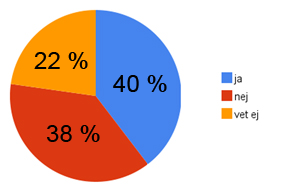
معاني الكلمات على الشكل:
| اللغة السويدية | اللغة العربية |
| ja | نعم |
| nej | لا |
| vet ej | لا أعرف |
تستخدم الرسوم البيانية الدائرية بصورة أكبر في توضيح نِسب قيّم مختلفة من الكل (الجزء من الكل). على سبيل المثال قد تكون نسب الأصوات التي حصلت عليها الأحزاب السياسية المختلفة في إحدى الإنتخابات.
الرسم البياني الخطي
في الرسم البياني الخطي التالي يمكننا قراءت عدد الأهداف التي أحرزتها ثلاث فرق مختلفة في دوري كرة القدم:
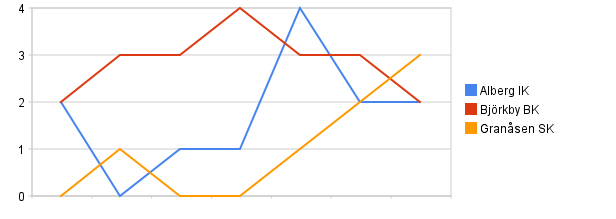
الكلمات السويدية على يمين الرسم عبارة عن أسماء الفُرق.
على طول المحور x في هذا الرسم البياني لدينا عدد المباريات التي لعبها كل فريق وعلى طول المحور y لدينا عدد الأهداف التي أحرزها كل فريق. نلاحظ أن نقاط بداية الخطوط تقع عند أقصى يسار الرسم البياني وهي عبارة عن عدد الأهداف التي أحرزها كل فريق في أول مباراة، بينما في أقصى اليمين لدينا عدد الأهداف التي أحرزها كل فريق في آخر مباراة له في الدوري.
باستخدام هذا الرسم البياني يمكننا بكل سهولة توضيح ما حدث لهذه الفرق الثلاثة في المباريات التي لعبتها في الدوري. وبصورة عامة غالبا ما تُستخدم الرسوم البيانية الخطية في عرض كيفية تغير الأشياء مع مرور الزمن. في المثال أعلاه عرضنا كيفية تغيّر عدد أهداف كل فريق مع مرور الزمن (بمرور المباريات).
مثال آخر لاستخدام الرسوم البيانية الخطية هو عرض نتائج دعم الناخبين للأحزاب السياسية في سلسلة من إستطلاعات الرأي – في هذه الحالة سيكون من السهل ملاحظة كيفية تغيّر نتائج الإنتخابات مع مرور الزمن، وهذا قد يكون مفيدا لأن ذلك سيساعد في إدراك كيفية سير الانتخابات القادمة على سبيل المثال.
الرسم البياني الشريطي
الرسم البياني الشرسطي التالي يوضح نفس نتائج الإستطلاع التي تم عرضها في الرسم الدائري أعلاه ولكن النسب المئوية غير موضحة في هذه الحالة:
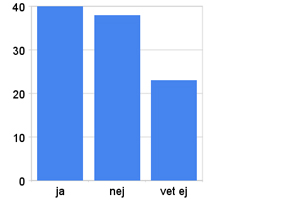
البيانات التي يتم عرضها على الرسوم البيانية الشريطية عادة ما لا تتكون من أعداد، كما في هذه الحالة لدينا بيانات تتكون من ثلاثة خيارات وهي الإجابة بــ: نعم - لا - لا أعرف.
الرسم البياني العمودي
هناك نوع آخر من الرسوم البيانية وهو الرسم البياني العمودي وهو يُستخدم لنفس الغرض المستخدم له الرسم البياني الشريطي، ولكن البيانات المُدخلة في هذه الحالة عبارة عن أعداد. على المخططات البانية العمودية يتم عرض تكرار القيّم المختلفة أي كيفية إنتشار القيّم المختلفة لنتائج أحد الإستطلاعات (دراسة إحصائية).
في الرسم البياني التالي تم توضيح كيفية إنتشار وقوع الحوادث في طريق معين وعددها في السنة خلال فترة مداها 15 سنة:
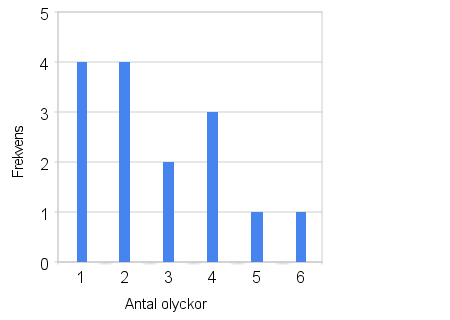
معاني الكلمات على الشكل:
| اللغة السويدية | اللغة العربية |
| Antal olyckor | عدد الحوادث |
| Frekvens | التكرار |
من الرسم يمكننا ملاحظة أن وقوع حادث واحد فقط في السنة تكرر أربع مرات, وأيضا وقوع حادثتين في السنة تكرر أربع مرات، ووقوع ثلاث حوادث في السنة تكرر مرتين وهكذا.
المدرج التكراري (Histogram)
يُستخدم المدرج التكراري (histogram) عندما تحتوي المادة المُراد توضيحها على عدة قيم مختلفة تحتاج للتقسيم لفئات مختلفة. في المدرج التكراري عادة ما يتم عرض البيانات التي تتكون من أعداد.
كمثال على ذلك يمكننا إستخدام المدرج التكراري لعرض أعمار عمال إحدى الشركات التي يعمل بها 20 عاملا، حيث كانت أعمارهم:
23, 25, 25, 28, 33, 38, 42, 48, 26, 31, 32, 38, 53, 51, 44, 45, 26, 37, 42 و35 عام.
وكانت النتيجة كما في المدرج التكراري التالي
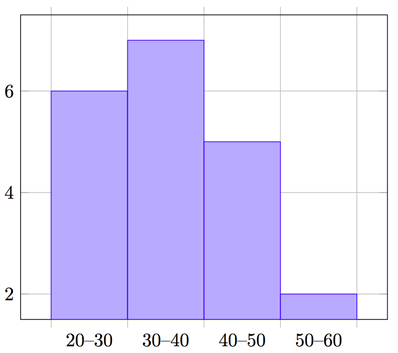
على محور x لدينا مدى الأعمار بحيث كل عمود يُمثل مدى معين من الأعمار، وعلى محور y لدينا عدد الذين أعمارهم في نفس المدى. في هذا المثال يمكن أن يظهر المدرج التكراري (histogram) بشكل مختلف وذلك بناءا على مدى الأعمار المُستخدم.
فيديوهات الدرس (باللغة السويدية)
في هذا الفيديو نستعرض الرسم البياني الدائري.
في هذا الفيديو نستعرض الرسم البياني الخطي.
في هذا الفيديو نستعرض الرسم البياني الشريطي.
في هذا الفيديو نستعرض المدرج التكراري (histogram).
في هذا الفيديو سنمر على مفهوم الإحصاء الخادع.
هنا سنواصل في شرح الإحصاء الخادع مع مثال آخر.
