الدوال الخطية

في القسم السابق تعرفنا على مفهوم الدالة ورأينا كيف يمكن استخدامها لوصف العلاقة بين المتغيرات. في هذا القسم سنتعلم أحد أنواع الدوال الشائعة والتي يمكن إستخدامها لوصف العديد من المواقف المختلفة.

إذا كانت جميع نقاط الدالة عبارة عن خط مستقيم عند رسمها على نظام الإحداثيات عندئذ تُسمى الدالة دالة خطية.

فيما يلي مثال على الدالة الخطية البسيطة:

$$y(x)=x+5$$

تعتمد قيمة الدالة (قيمة \(y\)) على قيمة \(x\) التي سندخلها.

إذا كان على سبيل المثال \(x = 2\) فستكون \(y = 2 + 5 = 7\). وإذا كانت \(x = 5\) فستكون \(y = 5 + 5 = 10\)

إذا أدخلنا قيّم مختلفة لـ \(x\) يمكننا أن نلاحظ العلاقة بصورة واضحة كما في جدول القيّم التالي:

\(x\)	\(y(x)\)
0	5
1	6
2	7
3	8
4	9

معادلة الخط المستقيم

فيما يلي الصورة العامة للدالة الخطية:

$$y=kx+m$$

حيث أن \(x\) و \(y\) متغيرات، \(k\) و \(m\) ثوابت تحكم العلاقة بين المتغيرات.

تُسمى الصيغة أعلاه بمعادلة الخط المستقيم. أي دالة تأخذ هذه الصورة يمكن رسمها في شكل خط مستقيم.

إذا كان \(k = 1\) فسنحصل على الحد \((1 \cdot x)\), مما يعطي \(x\). بالتالي:

$$y(x)=1\cdot x+5=x+5$$

الثوابت \(k\) و \(m\)

كما ذكرنا سابقا أن \(x\) و \(y\) هي عبارة عن متغيرات، فإن قيمة \(y\) (قيمة الدالة) تتغير وفقا لقيمة المتغير \(x\). فما معنى الثوابت \(k\) و \(m\)؟

يُسمى \(k\) بالميل ويمثل ميل الخط المستقيم.

عندما تكون قيمة \(k\) موجبة سيكون الخط مائل قطريا للأعلى يمين نظام الإحداثيات، ما يعني أن قيمة الدالة ستكون أكبر كلما زادت قيمة المتغير المستقل \(x\).

عندما تكون قيمة \(k\) سالبة سيكون الخط مائل قطريا للأسفل يمين نظام الإحداثيات، وفي هذه الحالة ستكون قيمة الدالة أصغر كلما زادت قيمة المتغير المستقل \(x\).

فإذا كان \(k = 0\) سيكون الخط أفقي متوازيا مع محور \(x\). (لاحظ عندما يكون \(k = 0\) فإن قيمة الدالة لا تعتمد على قيمة المتغير المستقل - ستكون قيمة الدالة في هذه الحالة قيمة ثابته بغض النظر عن قيمة المتغير المستقل).

تُسمى \(m\) بالحد الثابت كما تٌسمى أيضان بالجزء المقطوع من محور \(y\) وهي التي تحدد أين يتقاطع الخط مع محور \(y\). وقيمة \(m\) هي قيمة \(y\) للنقطة الإحداثية التي يكون عندها \(x = 0\) أي عندها يتقاطع الخط مع المحور \(y\).

إذا كانت قيمة \(m\) موجبة سيقطع الخط محور \(y\) أعلى نقطة الأصل وإذا كانت قيمة \(m\) سالبة سيكون التقاطع أسفل نقطة الأصل. أما إذا كان \(m = 0\) عادة ما نتجاهل قيمة \(m\) وفي هذه الحالة سيمر الخط بنقطة الأصل (أي النقطة \((0, 0)\)).

في مثال الدالة أعلاه نلاحظ أن \(k = 1\) كما نلاحظ أيضا أن قيمة \(m\) هي 5. بالتالي إذا رسمنا خط هذه الدالة على نظام الإحداثيات سينتج خط مستقيم يتقاطع مع محور \(y\) عند النقطة \((0, 5)\), أي النقطة التي يكون فيها \(x = 0\) و \(y = 5\).

حساب ميل الخط المستقيم

يُرمز لميل الخط المستقيم بالحرف k كما ذكرنا أعلاه, كما يُسمى أيضا بمعامل الإنحدار. فيما يلي سنتعلم كيف يمكننا حساب الميل.

إذا علمنا نقطتين على الخط المستقيم, \((x_1,y_1)\) و \((x_2,y_2)\) يمكننا إيجاد الميل بإستخدام الصيغة التالية:

$$k=\displaystyle\frac{\Large\text{y التغيّر في}}{\Large\text{x التغيّر في}}=\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}$$

لنوضح ذلك بحساب قيمة k لمعادلة المثال السابق. لنأخذ النقطتين (0,5) و (3,8) من الجدول أعلاه. دعونا نفترض أن النقطة الأولى هي النقطة 1 والنقطة الثانية هي النقطة 2.

$$\begin{align} (x_1,y_1) & =(0,5) \\ (x_2,y_2) & =(3,8)\end{align}$$

بتعويض هذه النقاط في الصيغة أعلاه يمكننا الحصول على:

$$k = \frac{y_2-y_1}{x_2-x_1} =  \frac{8-3}{5-0} =  \frac{5}{5} = 1 $$

وهذا صحيح لأن المعادلة كانت y(x)=x+5.

صيغة الميل-k للمعادلة الخطية

إذا كان لدينا نقطتين من النقاط التي يمر بها الخط المستقيم يمكننا إيجاد معادلته في صورة y=kx+m. أولا علينا إيجاد قيمة k, الخطوة التالية إيجاد قيمة m (الجزء المقطوع من y) والخطوة الأخيرة تعويض قيمة كل من k و m  في صيغة الميل للمعادلة الخطية. لنوضح ذلك بالمثال التالي:

نواصل مع نفس المثال السابق, أي بإستخدام النقطتين (0,5) و (3,8). تم حساب قيمة k أعلاه وكانت 1, بالتالي الخطوة التالية حساب قيمة m. يتم ذلك بتعويض قيمة k في معادلة الخط ثم نحلها لإيجاد m:

$$y=kx+m=1\cdot x+m=x+m$$

$$m=y-x$$

بما أنه لدينا نقطتين معلومتين من النقاط التي يمر بها الخط يمكننا إختيار أي منهما وتعويضها في هذه المعادلة , لنختار النقطة (3,8):

$$m=8-3=5$$

الآن لدينا (k = 1) و (m = 5), ويمكن تعويضهما في معادلة الخط المستقيم كما يلي:

$$y=kx+m=1\cdot x + 5=x+5$$

إذن معادلة الخط هي (y = x + 5), وهي المعادلة الخطية في صيغة الميل-k.

صيغة المعادلة الخطية بدلالة نقطة معلومة

إذا علمنا كل من قيمة k ونقطة من النقاط التي يمر بها الخط المستقيم يمكننا إيجاد معادلة هذا الخط المستقيم ويتم ذلك بإستخدام صيغة النقطة المعلومة. صيغة معادلة الخط المستقيم بدلالة النقطة المعلومة هي:

$$(y-y_1)=k(x-x_1)$$

لتسهيل مفهوم صيغة النقطة المعلومة يمكننا حل مثال على ذلك, لنستخدم نفس المثال السابق. بما أن صيغة حساب الميل هي:

$$k=\frac{y_2-y_1}{x_2-x_1}$$

ونعلم أن  (k=1) والنقطة ((x₁,y₁)=(3,8)). وأيضا جميع النقاط التي يمر بها هذا الخط المستقيم تنطبق عليها الصيغة التالية:

$$k=\frac{y-y_1}{x-x_1}$$

يمكن تعويض قيمة كل من k والنقطة (x₁,y₁) والحصول على:

$$1=\frac{y-8}{x-3}$$

وبالضرب العكسي يمكننا الحصول على:

$$1\cdot(x-3)=y-8$$

وهي معادلة هذا الخط المستقيم بدلالة النقطة المعلومة. ومن هذه المعادلة يمكننا إيجاد صيغة الميل-k لمعادلة هذا الخط المستقيم وذلك بوضع y في الطرف الأيسر كما يلي:

$$y=x-3+8=x+5$$

رسم الدوال الخطية

بما أن المعادلة خطية فهذا يعني أنه إذا أخذنا نقطتين ورسمنا خط بينهما فإن هذا الخط سيستمر بنفس الانحدار (الميل) قبل وبعد كل نقطة. يمكن أن نبدأ بالنقطة \((0, 5)\) من المثال السابق وهي النقطة التي يقطع فيها الخط محور \(y\). ثم نأخذ نقطة أخرى فلتكن مثلا النقطة الأخيرة من جدول القيّم أعلاه ثم نوصل بين النقطتين بخط كما يلي:

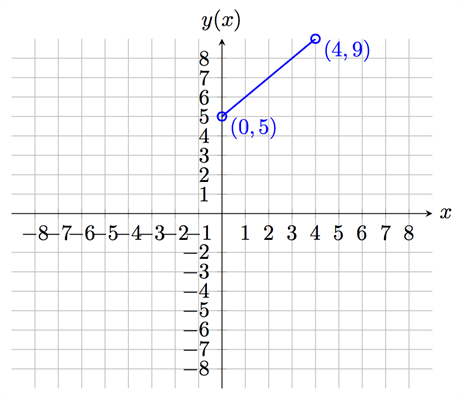
ومن ثم من كل نقطة يمكننا رسم امتداد لهذا الخط ونحصل على خط الدالة \(y (x) = x + 5\) كاملا كما يلي:

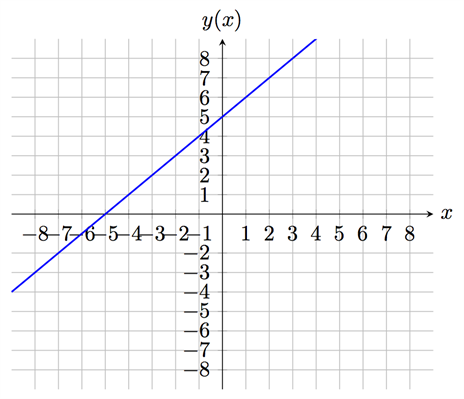
إذا افتقدت الدالة قيمة \(m\) (أي أن قيمة \(m\) تساوي صفر) يمكن كتابة الدالة كما يلي:

$$y=kx$$

وتُسمى هذه الحالة الخاصة من الدوال الخطية بالتناسب. في القسم السابق قابلنا مثال على التناسب وهو معادلة راتب إيناس كدالة في عدد الساعات التي عملتها. وفي هذا المثال كان راتبها يتناسب مع عدد الساعات التي عملتها أي كلما زاد عدد الساعات زاد راتبها.

فيديوهات الدرس (بالسويدية)

في هذا الفيديو سنمر على الدوال الخطية وقيمة \(k\).

في هذا الفيديو سنمر على الدوال الخطية وقيمة \(m\).

في هذا الفيديو سنمر على كيفية إيجاد معادلة الخط المستقيم بإستخدام صيغة الميل \(k\).

في هذا الفيديو سنمر على كيفية إيجاد معادلة الخط المستقيم بإستخدام صيغة نقطتين معلومتين.

الوسيلة المساعدة (آلة حاسبة)

هنا تم استخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).

الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريبا.