الكرة، المخروط والهرم

في القسم السابق مررنا على كيفية حساب حجم بعض الأجسام الثلاثية الأبعاد الأساسية: شبه المكعب، المنشور والاسطوانة. في هذا القسم سنواصل مع طُرق حساب حجم ومساحة كل من: الكرة، المخروط والهرم.

الكرة / الجسم الكروي

الكرة أو الجسم الكروي هي جسم ثلاثي الأبعاد له شكل الكرة ويُسمى سطحها بالسطح الكروي وهو السطح الخارجي للكرة (المشار إليه بكلمة klotyta في الشكل أدنا). أكبر دائرة يمكن أن تحتويها الكرة هي الدائرة التي تتمركز مع الكرة أي أن مركزها هو مركز الكرة نفسه وهي الدائرة المرسومة بالخط المتقطع في الشكل أدناه. نصف القطر هو المسافة بين مركز الكرة وسطح الكرة كما يُشار إليه بكلمة "radie" في الشكل أدناه.

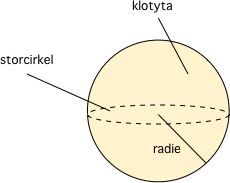
يتم حساب مساحة الكرة (مساحة سطح الكرة) باستخدام الصيغة التالية:

$$A_\text{الكرة}=4\cdot \pi \cdot r^{2}$$

ويتم حساب حجم الكرة وفقا للصيغة التالية:

$$V_\text{الكرة}=\frac{4\cdot \pi \cdot r^{3}}{3}$$

المخروط

يتألف المخروط من قاعدة مسطحة وسطح جانبي. يتشكل السطح الجانبي للمخروط باتصال جميع نقاط قاعدته بنقطة تقع على بعد معين من القاعدة.

المخروط الشائع هو المخروط الدائري وهو حالة خاصة من المخاريط، وهو مخروط قاعدته دائرية (يقع رأس المخروط الدائري فوق مركز الدائرة مباشرة، ويٌسمى بالمخروط الدائري المستقيم - وهذا ما نعنيه في حياتنا اليومية عندما نقول "مخروط"). وفي الحالات التي يكون فيها شكل القاعدة مضلع يُسمى بالهرم.

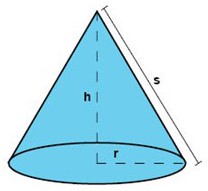
حجم المخروط الدائري يساوي تماما ثُلث حجم الأسطوانة التي لها نفس القاعدة والإرتفاع. لذا صيغة حجم المخروط الدائري هي:

$$V_\text{المخروط الدائري}=\frac{\pi \cdot r^{2}\cdot h}{3} $$

ويتم تحديد مساحة السطح الجانبية للمخروط باستخدام المسافة من محيط القاعدة الى رأس المخروط ونصف قطر القاعدة ويتم حسابها كما يلي:

مساحة السطح الجانبية للمخروط \(\pi\cdot r\cdot s=\)

$$Mantelarea_{cirkulär\,kon} = \pi\cdot r\cdot s$$

الهرم

كما ذكرنا أعلاه الهرم هو حالة خاصة للمخروط، حيث أن شكل القاعدة مضلع. ويمكن أن تأخذ قاعدة الهرم أشكال مختلفة، وشكلها قد يكون ثلاثي، رباعي أو خماسي الأضلاع، ولكن الأهرامات الأكثر شيوعا هي التي تكون قاعدتها في شكل مستطيل, مربع أو مثلث كما في الشكل التالي.

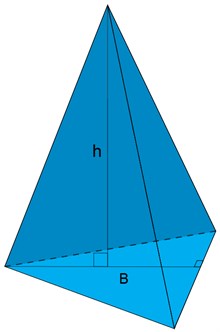
بنفس طريقة تناسب حجم المخروط الدائري مع حجم الأسطوانة، يتناسب حجم الهرم مع حجم المنشور. أي أن حجم المنشور ثلاثة أضعاف حجم الهرم الذي له نفس الارتفاع والقاعدة. ويتم حساب حجم الهرم كما يلي:

$$V_\text{المنشور}=\frac{\text{الإرتفاع}\cdot \text{القاعدة}} {3} = \frac{B\cdot h}{3}$$

فيديوهات الدرس (بالسويدية)

كيفية حساب حجم ومساحة الكرة.

كيفية حساب حجم ومساحة المخروط الدائري.

وسيلة مساعدة

في هذا التمرين تم استخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).

الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريبا.