حل المعادلات بيانيا
إذا كان لدينا دالة معينة ومُعطى معها قيمة أحد المتغيرات يمكننا الحصول على معادلة رياضية. يمكن حل المعادلات عن طريق الحل الجبري كما رأينا سابقا أو عن طريق الحل البياني وهو ما سندرسه في هذا القسم.
يتم حل المعادلة بيانيا عن طريق تحويل كل طرف من طرفي الدالة إلى دالة منفصلة لكي نحصل على دالتين، ومن ثم يتم رسمهما على نفس نظام الإحداثيات. بالتالي النقطة التي يتقاطع عندها الخطان أو المنحنيان البيانيان هي حل المعادلة وذلك لأن طرفي المعادلة متساويين عند هذ النقطة \(VL = HL\) أي أن الطرف الأيسر يساوي الطرف الأيمن.
يمكن توضيح ذلك عمليا بكل سهولة كما في المثال التالي
لنفترض أننا نريد حل المعادلة التالية بيانيا:
$$5x=87$$
بالتالي يمكننا الحصول على الدالتين أدناه
$$\left\{\begin{matrix} y_{1}=5x \\ y_{2}=87 \end{matrix}\right.$$
يمكن رسمهما بيانيا على نظام الإحداثيات كما يلي:
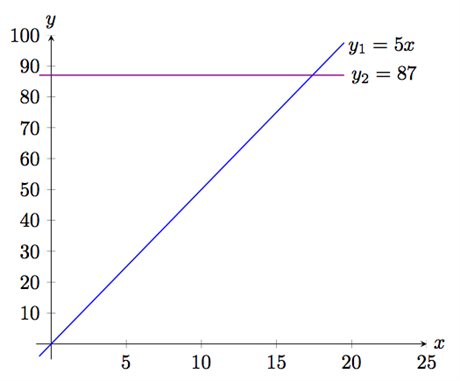
إحداثيات نقطة تقاطع الخطين هي \((17,4\,;\,87)\) وهي حل المعادلة، أي أن \(x = 17,4\).
لنرى مثال آخر:
إذا كان لدينا بدلا من ذلك المعادلة التالية
$$x^{3}=87$$
والتي يمكننا حلها بيانيا، فمن ثم يمكننا الحصول منها على دالتين بنفس طريقة المثال السابق:
$$\left\{\begin{matrix} y_{1}=x^{3} \\ y_{2}=87 \end{matrix}\right.$$
أيضا يمكن رسمهما بيانيا على نظام الإحداثيات كما يلي:
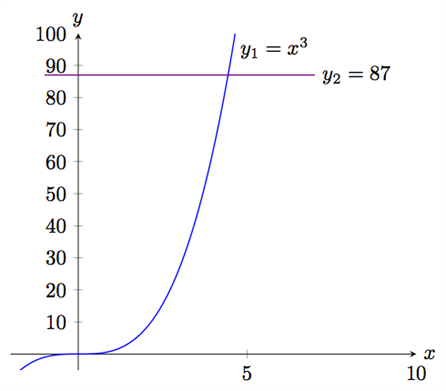
إحداثيات نقطة تقاطع الخطين هي \((4,43\,;\, 87)\) بالتقريب، ما يعطينا حل المعادلة وهو \(x ≈ 4,43\).
فيديوهات الدرس (بالسويدية)
فيما يلي سنشرح كيف يمكننا حَل المعادلات باستخدام الرسوم البيانية (حَل المعادلات بيانياً).
