الإستلزام، التكافؤ والبرهان
في هذا القسم سنتعمق قليلا ونتعرف على كيفية مناقشة وإستنتاج النظريات والمفاهيم الرياضية وإثبات صحتها.
الإستلزام
إذا وقع الحدث \(A\) وأدى إلى وقوع الحدث \(B\) فهذا ما يُسمى بالإستلزام بمعنى أن حدوث \(B\) يستلزم حدوث \(A\), ويرمز للإستلزام بسهم \((A \to B)\) وتُقرأ \(A\) يؤدي الى \(B\).
مثال على الاستلزام الرياضي: حدوث (\(A\): شكل رباعي به ثلاث زوايا قائمة), مما يؤدي إلى حدوث \(\leftarrow\) (\(B\): الركن الرابع لهذا الشكل الرباعي عبارة عن زواية قائمة) وتُكتب \(A \to B\).
الاستلزام العكسي يعني أن الاستلزام يعمل أيضا في الاتجاه الآخر، أي إذا كان \(A \to B\) فإن \( B \to A \). ولكن لا ينطبق على كل الحالات أن \( B \to A \) إذا كان \(A \to B\).
وفيما يلي مثال على ذلك:
إذا كان الحدث
\(A: x = 3\)
والحدث
\(B:x^2 = 9\)
يمكننا بالطبع أن نقول أن \(A \to B\) ولكن إذا عكسنا الاستلزام إلى (\( B \to A \)) فهذا خطأ, لأنه إذا كان \(x^2 = 9\) فلا ينطبق فقط أن \(x = 3\) لأنه يمكن أيضا أن تكون \(x = -3\). بالتالي لا ينطبق الاستلزام العكسي في جميع الحالات.
بنفس الطريقة يمكننا أخذ أمثلة من حياتنا اليومية:
\(A\): إنها تمطر بالخارج.
\(B\): أحمل معي المظلة الشمسية عندما أخرج.
على الرغم من صلاحية \(A \to B\) (عندما تكون ممطرة بالخارج, سأحمل شمسيتي عندما اخرج), ولكن لا يستلزم أن \( B \to A \) (فإذا حملت شمسيتي عند الخروج فقد لا تمطر بالخارج).
التكافؤ
إذا انطبق الاستلزام في كلا الاتجاهين سيُرمز له بسهم مزدوج: \((\leftrightarrow)\), وهذا ما يُسمى يتكافؤ الحدثين أو الإدعائين.
مثال:
\(x = -2 \leftrightarrow 4 + 2x = 0\)
البرهان
البرهان أو الإثبات الرياضي يعني التحليل أو التعليل المنطقي الذي يقود إلى نتائج أو إستنتاجات منطقية، بناءاً على فرضيات منطقية سليمة وتحليل صحيح. الطريقة الحالية للتعامل مع البراهين الرياضية تم تطويرها من قِبل عالم الرياضيات اليوناني إقليدس حوالي 300 عام قبل الميلاد. وتعتمد طُرُقه على تعريف البديهيات الأولية في أولاً، ثم استخدام البرهان لإشتقاق النظريات منها.
إثبات أو برهان نظرية فيثاغورس
نريد إثبات صحة نظرية فيثاغورس. غالبا ما يتم إثبات بعض النظريات بعدة طرق مختلفة.
لإثبات صحة نظرية فيثاغورس سنبدأ بمناقشة مثلث قائم الزاوية كما في الشكل أدناه. الوتر هو الضلع الذي طوله \(c\) والضلعين القائمين للمثلث أطوالهما \(a\) و \(b\) وحدة طولية.
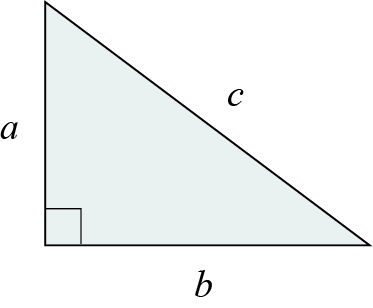
الآن نقوم بتوسيع هذا الشكل عن طريق رسم ثلاث مثلثات أخرى مشابهة للمثلث الأول، بحيث تُشكل الأضلاع القائمة لهذه المثلثات الأربع معا شكل رباعي كبير طول ضلعه \((a + b)\) وحدة طولية، بينما تبني أوتارها شكل رباعي أصغر طول ضلعه \(c\) وحدة طولية وفقا للشكل التالي.
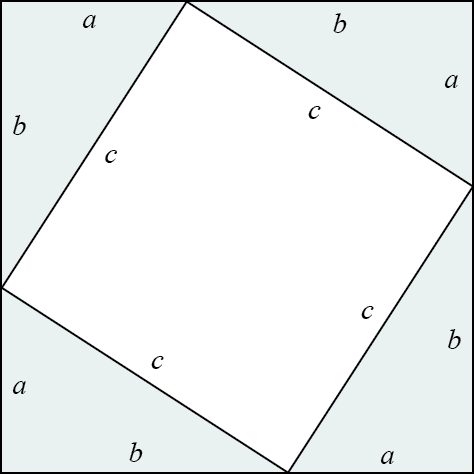
إذا نظرنا إلى الشكل الرباعي في المنتصف سنلاحظ أن جميع أضلاعه متساوية في الطول (\(c\) وحدة طولية)، وزواياه متماثلة في المقدار. وفي هذه الحالة يجب أن يكون مقدار كل منها 90 درجة، لأن مجموع زوايا الشكل الرباعي 360 درجة. بالتالي لدينا مربع في المنتصف.
الخطوة القادمة هي تحديد مساحة الشكل الرباعي الكبير، الذي يجب أن يكون أيضا مربع طول ضلعه \((a + b)\) وحدة طولية، وهذا يعني أن مساحته هي \((a + b)^ 2\) وحدة مساحة.
هذه المساحة يمكننا إيجادها بطريقة أخرى:
لدينا أربعة مثلثات متطابقة (متماثلة)، مساحة كل منها
$$\frac{a\cdot b}{2}$$
ومنها يمكننا إيجاد المساحة الكلية للمثلثات الأربع معا كما يلي
$$\frac{4\cdot a\cdot b}{2}=2ab$$
أيضا المربع الصغير في منتصف الشكل طول ضلعه \(c\) وحدة طولية بالتالي مساحته هي \(c^ 2\) وحدة مساحة.
من الشكل نلاحظ أن مساحة المربع الكبير هي عبارة عن مساحة المربع الصغير زائدا مساحة المثلثات الأربعة معا، بالتالي يمكننا كتابة العلاقة التالية:
$$(a+b)^2=2ab+c^2$$
بإعادة كتابة الطرف الأيسر سنحصل على
$$a^2+2ab+b^2=2ab+c^2$$
بطرح \(2ab\) من الطرفين يمكننا الحصول على
$$a^2+b^2=c^2$$
وهي العلاقة المطلوب إثباتها.
فيديو الدرس (بالسويدية)
فيما يلي سنشرح عمليتي الإستلزام implikation والتكافؤ ekvivalens.
في هذا الفيديو سنشرح طريقة إثبات قانون الزاويه الخارجيه.
