المتوسط، الوسيط، المنوال وعرض التغيّر
في القسم السابق تعلمنا كيف يمكننا تفسير الرسوم البيانية وكل نوع من هذه الرسوم البيانية المختلفة يمكن أن يكون مفيد جدا إذا تم إختيار النوع المناسب بناءا على المعلومات التي نريد توضيحها بيانيا. في هذا القسم سنناقش بعض المقاييس الإحصائية التي يمكن أن تساعدنا أيضا في وصف البيانات الإحصائية.
المتوسط
القيمة المتوسطة هي القيمة التقريبية التي تُمثل مجموعة من القيّم. كيفية تمثيل القيمة المتوسطة لمجموعة من القيّم يختلف من موقف إلى موقف، ولكن في أغلب الأحيان هي طريقة مناسبة لتلخيص مجموعة من القيّم بالتقريب.
دعونا نشرح بصورة أوضح خلال المثال التالي
خلال أحد الأسابيع كانت أمينة تركض مهرولة كل مساء (تجري بسرعة بطيئة لتحسين لياقتها). كانت تركض ما بين 7 الى 12 كلم، ولكي تتذكر المسافة التي ركضتها قامت بتسجيل المسافات التي قطعتها في جدول. إذا سألها شخص ما عن المسافة التي ركضتها في كل أمسية فقد يكون من الصعب عليها إستحضار المسافات السبع.
الطريقة الأسهل هي تحديد قيمة تقريبية واحدة لوصف المسافات التي ركضتها خلال أمسيات هذا الأسبوع. إذا حسبنا المسافة الكلية التي ركضتها ثم قسمناها علـى 7 أيام سنحصل على مقدار المسافة الكلية موزعة على أيام الأسبوع بالتساوي:
$$\frac{7+8+7,5+8+12+7,5+9}{7}=\frac{59}{7}\approx 8,4 \,km $$
أي أن أمينة يمكنها أن تجيب على الشخص الذي سألها بأنها كانت تركض بمعدل 8,4 كلم في الليلة خلال هذا الأسبوع.
وهذا ما يُسمى بالقيمة المتوسطة. الصيغة الرياضية لحساب القيمة المتوسطة هي:
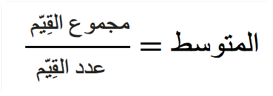
قارن حاصل ضرب القيمة المتوسطة فـي عدد الأيام مع المسافة الكلية التي ركضتها أمينة:
$$8,4+8,4+8,4+8,4+8,4+8,4+8,4\,km=$$
$$=7\cdot 8,4\,km\approx 59\,km$$
ولهذا يمكننا أستخدام القيمة المتوسطة كقيمة تقريبية لتمثل مجموعة من القيّم.
الوسيط
في بعض الأحيان قد تكون القيمة المتوسطة قيمة منحرفة وتعكس صورة غير مضبوطة عن الصورة العامة، على الرغم من صحة حسابها رياضيا. قد يكون هذا على سبيل المثال بسبب أن أحدى هذه القيّم كبيرة جدا أو صغيرة جدا مقارنة بالقيّم الأخرى في المجموعة، فهذا قد يؤثر على قيمة المتوسط بشكل كبير وفي هذه الحالة ستكون قيمة المتوسط مضللة في تقييم القيّم الأخرى.
في مثل هذه الحالات غالبا ما تكون قيمة الوسيط هي الأكثر إستخداما. الوسيط هو القيمة التي تقع في منتصف مجموعة من القيّم المُرتبة حسب الحجم أو المقدار.
سنوضح هذا في المثال التالي
كان ميشيل يتجول في الجبال لمدة خمس أيام وكان كل يوم يسير مسافة 40 كلم تقريبا ما عدا يوم واحد قطع مسافة 5 كلم فقط.
| اليوم | المسافة (كلم) |
| 1 | 38 |
| 2 | 40 |
| 3 | 41 |
| 4 | 5 |
| 5 | 41 |
سنقارن قيمة المتوسط بقيمة الوسيط, لنبدأ بحساب المتوسط:
المتوسط =
$$=\frac{38+40+41+5+41}{5}=33\,km$$
أي أن القيمة المتوسطة للمسافة التي قطعها هي 33 كلم في اليوم، ولكن لأنه سار مسافة 5 كلم فقط في أحد الأيام فهذا أدى الى إنخفاض قيمة المتوسط بشكل كبير (فإذا حسبنا متوسط الأربعة أيام التي قطع فيها ميشيل مسافات طويلة فستكون قيمة المتوسط 40 كلم).
قد تعطي قيمة الوسيط صورة أقرب للمسافة التي قطعها ميشيل في اليوم. نبدأ بترتيب القيُم المُعطية في الجدول أعلاه ترتيب تصاعدي:
$$5,\: 38,\: 40,\: 41,\: 41$$
القيمة الوقعة في منتصف مجموعة هذه القيّم هي 40. هذه القيمة تمثل قيمة الوسيط لمجموعة هذه القيّم. أي أن الوسيط هو 40 كلم مما يعني أن ميشيل قطع مسافة 40 كلم في اليوم تقريبا، إذا نظرنا إلى القراءات يمكن اعتبار أن الوسيط يُمثل هذه القيّم بصورة أفضل.
في بعض الأحيان عندما نقوم بترتيب القيّم قد نلاحظ أنها لا تحتوي على قيمة تقع في المنتصف وذلك عندما يكون لدينا عدد زوجي من القيّم.
وهذا ينطبق على مجموعة القيّم التالية
$$2,\: 2,\: 4,\: 5,\: 6,\: 7,\: 7,\: 8$$
في مثل هذه الحالات يمكننا الحصول على قيمة الوسيط بحساب القيمة المتوسطة للقيمتين الواقعتين في المنتصف. في المثال أعلاه قيمتي المنتصف هما 5 و6 ويمكن حساب الوسيط كما يلي:
الوسيط =
$$=\frac{5+6}{2}=5,5$$
المنوال
تحديد المنوال هو طريقة أخرى لوصف مجموعة من القيّم وهو عبارة عن القيمة الأكثر تكرارا في مجموعة القيّم.
إذا رجعنا إلى مثال حركة ميشيل على الجبال يمكننا إستنتاج قيمة المنوال للمسافات التي مشاها خلال هذه الأيام. نقوم أولا بترتيب القيّم حسب طول المسافة لكي تكون القيّم المتشابهة بجوار بعضها البعض.
$$5,\: 38,\: 40,\: 41,\: 41$$
الآن نلاحظ أن القيمة 41 تكررت مرتين في مجموعة هذه القيّم بينما كل من القيّم الأخرى حدثت مرة واحدة فقط. أي أن قيمة المنوال هي 41, وهذا يعني أن المسافة الاكثر تكرارا من بين المسافات التي قطعها ميشيل في اليوم هي 41 كلم.
عرض التغيُّر
عرض التغيّر هو مقياس آخر يمكن أن يعطينا معلومات غير مباشرة عن مجموعة من القيّم. عرض التغيّر هو الفرق بين أكبر قيمة وأصغر قيمة في مجموعة القيّم. مثلا عندما يكون عرض التغيّر كبير في مجموعة من القيّم فغالبا ما تكون قيمة المتوسط خادعة (مضللة) في هذه الحالة، وذلك لأن القيّم ستكون موزعة (منتشرة) على نطاق واسع. ويعتمد مدى تأثير عرض التغيّر على سياق المسألة.
مثال على ذلك
في الانتخابات الأخيرة للبرلمان السويدي كان عمر أصغر شخص من الذين صوتوا في هذه الانتخابات 18 سنة وأكبر شخص 104 سنة. مما يعني أن أقل قيمة هي 18 سنة وأكبر قيمة هي 104 سنة.
ويمكننا حساب عرض التغيّر في أعمار الذين صوتوا في الانتخابات كما يلي:
عرض التغيّر يساوي
$$=104-18=86$$
إذن فرق العمر بين أكبر وأصغر شخص هو 86 سنة.
فيديوهات الدرس (باللغة السويدية)
في هذا الفيديو سنستعرض المقاييس الموضعيه ومقياس عرض التغيُّر (الإنتشار).
في هذا الفيديو سنشرح مفاهيم المقاييس الموضعية الثلاثة, المتوسط, الوسيط والمنوال.
هنا سنحل ثلاثة واجبات بحيث نوجد فيها قيمة كل من المتوسط, الوسيط والمنوال.
الوسيلة المساعدة (آلة حاسبة)
هنا تم إستخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).
الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريبا.
