شبه المكعب، المنشور والاسطوانة

في القسم السابق مررنا على كيفية حساب محيط ومساحة بعض الأشكال الثنائية الأبعاد المعروفة. في هذا القسم سنرى كيف يمكننا حساب حجم بعض الأجسام الثلاثية الأبعاد المعروفة: شبه المكعب، المنشور والاسطوانة.

شبه المكعب

شبه المكعب هو شكل ثلاثي الأبعاد يحتوي على زوايا قائمة فقط في أركانه الثمانية، كما هو موضح بالشكل أدناه. يمكنك أن تتخيل أن شبه المكعب له شكل كشكل صناديق الأحذية الجديدة أو أحجار البناء.

أيضا يمكنك أن تتخيل أن لديك شكل ثنائي الأبعاد في شكل مستطيل في الأسفل ثم نقوم ببناء هذا المستطيل الى الأعلى حتى يصبح له ارتفاع معين (كغرفة أو صندوق مثلا) وبذلك يكون لدينا شكل ثلاثي الأبعاد وهو شبه المكعب.

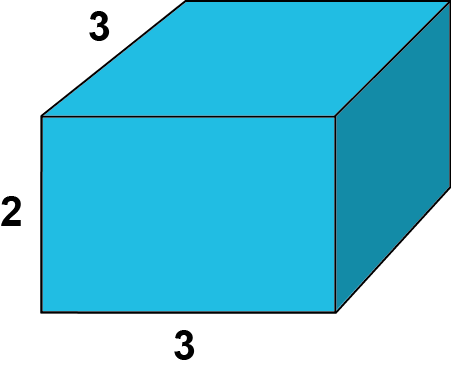
وفقا للتفكير بهذه الطريقة تم بناء الشكل أعلاه، وفي هذه الحالة تم إنشاء مستطيل سطحي طول كل من ضلعيه 3 (مربع)، ثم تم إنشاء شبه المكعب من خلال بناء ارتفاع الشكل الذي يبلغ طوله 2.

فإذا ضربنا مساحة سطح شبه المكعب فـي هذا الارتفاع سنحصل على حجم شبه المكعب (V).

V_{شبه المكعب} = الطول \(\cdot\) العرض \(\cdot\) الإرتفاع = مساحة القاعدة \(\cdot\) الإرتفاع

$${V}_{rätblock}=längden\cdot bredden\cdot höjden=basarean\cdot höjden$$

يُقاس الحجم بالوحدات المُكعبة. فعندما تكون أضلاع شبه المكعب بوحدة المتر سيكون حجمه بالمتر المكعب (م\(^3\)). واحد متر مكعب يساوي حجم مُكعب طول ضلعه 1 متر. المُكعب هو حالة خاصة من شبه المُكعب الذي جميع أضلاعه متساوية في الطول.

إذا كانت وحدة الطول في الشكل أعلاه بالمتر، فمن ثم يمكننا من خلال صيغة الحجم الحصول على الحجم كما يلي:

$$V=3\cdot 3\cdot 2=18m^3$$

تماما كما في حالة وحدات المساحة يمكننا توضيح كيفية التحويل بين الوحدات المختلفة في حالة الحجم:

$$1\,m^{3}=1(10\,dm)^{3}=1\cdot 10^{3}\;dm^{3}=1000\;dm^{3} $$

الوحدة باللغة السويدية	الوحدة باللغة العربية
\(m^3\)	م\(^{3}\)
\(dm^3\)	دسم\(^{3}\)

المنشور

المنشور هو جسم ثلاثي الأبعاد، سطح قاعدته لها شكل المُضلع (كخُماسي الأضلاع مثلا) وله ارتفاع معين. في الحقيقة شبه المكعب هو حالة خاصة من المنشور الذي يكون شكل قاعدته عبارة عن مستطيل؛ يمكن أن يكون للمنشور عدة أشكال مختلفة حسب قاعدته، على سبيل المثال يمكن أن تكون قاعدته مُثلثية (في شكل مثلث).

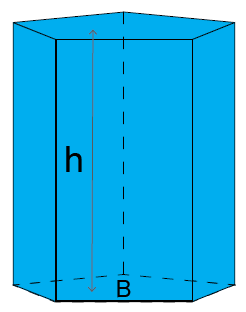
حجم المنشور يساوي مساحة سطح قاعدته مضروبة فـي ارتفاع المنشور:

$$V_{prisma}=A\cdot h$$

الأسطوانة

بنفس مفهوم شبه المكعب والمنشور الأسطوانة هي جسم ثُلاثي الأبعاد، ولكن الأسطوانة يجب أن يكون لها قاعدة في شكل دائري بالإضافة لإرتفاع معين.

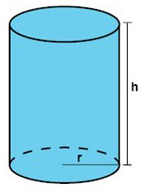
حجم الأسطوانة يساوي مساحة القاعدة الدائرية مضروبة فـي ارتفاع الأسطوانة.

$$V_{cylinder}=A\cdot h=\pi \cdot r^{2}\cdot h$$

مساحات السطح الكلية والجانبية

إذا قمنا بجمع مساحات القواعد مع مساحات الأسطح الجانبية للشكل المجسم سنحصل على ما يُسمى بمساحة السطح الكلية. المساحة التي تحيط بجوانب الأسطوانة (أو المخروط مثلا) تُسمى بمساحة السطح الجانبية. يمكننا أن نتخيل أن هذه المساحات السطحية هي عبارة عن الفواصل التي تُحدد جوانب الأجسام المختلفة.

فيديوهات الدرس (بالسويدية)

كيفية حساب حجم ومساحة الأشكال الثلاثية الأبعاد.

وسيلة مساعدة

في هذا التمرين تم استخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).

الآلات الحاسبة البيانية من الماركات الأخرى لديها نفس الوظائف تقريبا.