الأعداد الصحيحة والأعداد الطبيعية
توجد الأعداد في العديد من السياقات المختلفة والغرض المشترك بينها هو تمثيل الكميات المختلفة. هناك عدة أنواع مختلفة من الأعداد كما توجد مجموعات مختلفة من الأعداد وهي مفيدة في وصف العديد من الأشياء المختلفة. لاستخدام هذه الأعداد ومجموعاتها المختلفة بشكل صحيح من المهم جدا معرفة خصائص هذه الأعداد المختلفة وخصائص مجموعاتها. ومن المهم أيضا أن يتفق جميع الناس على كيفية الحساب بالأعداد لتوحيد المعنى.
الأعداد الطبيعية
الأعداد الطبيعية هي نوع من الأعداد التي استخدمها الناس منذ فترة طويلة.
الأعداد الطبيعية هي جميع الأعداد الصحيحة التي أكبر من أو تساوي الصفر: 0, 1, 2, 3, 4, ... إلخ، أي هي الأعداد الموجبة الصحيحة التي نستخدمها في الحساب الطبيعي، إبتدءا من الــ 1 ثم الأعداد الأكبر فالأكبر إلى مالا نهاية بالإضافة الى الــ 0 وهو عدد لا موجب ولا سالب ولكن بصورة عامة يُعتبر من العداد الطبيعية.
عادة ما يُرمز لمجموعة الأعداد الطبيعية بالحرف \(\mathbb{N}\).
$$\mathbb{N}=\left \{ 0,1,2,3,... \right \}$$
الأعداد الصحيحة
إذا أخذنا جميع الأعداد الطبيعية بالإضافة إلى جميع الأعداد الصحيحة السالبة سنحصل على مجموعة من الأعداد، والتي تُسمى بالأعداد الصحيحة الى يومنا هذا. تستمر الأعداد الصحيحة إلى مالا نهاية في كل من الاتجاه الموجب والاتجاه السالب.
يُرمز لمجموعة الأعداد الصحيحة بالحرف \(\mathbb{Z}\) (من الكلمة الألمانية Zahl والتي تعني "عدد")
$$\mathbb{Z}=\left \{ ..., -3, -2, -1, 0, 1, 2, 3,... \right \}$$
الآن سنتحدث عن بعض الخصائص الهامة للأعداد الصحيحة. هذه الخصائص سنشير اليها لاحقا في أقسام الدورة, لأنها مهمة ورئيسية في إجراء العمليات الحسابية مع الأعداد الصحيحة.
إذا كان كل من b ,a و c أعداد صحيحة، فإن الخصائص التالية ستكون صالحة:
| الخاصية | الجمع | الضرب |
| الإنغلاق | \(a+b\) عدد صحيح | \(ab\) عدد صحيح |
| التجميعية | \(a+(b+c)=(a+b)+c\) | \(a(bc)=(ab)c\) |
| التبادلية | \(a+b=b+a\) | \(ab=ba\) |
| التوزيعية | \(a(b+c)=ab+ac\) | \(a(b+c)=ab+ac\) |
| العنصر العكسي | \(a+(-a)=0\) | |
| العنصر المحايد | \(a+0=a\) | \(a \cdot 1=a\) |
| لا يوجد قاسم علـى الصفر | إذا كان \(ab=0\) فإما \(a=0\), \(b=0\) أو \(a\) و \(b\) يساوي صفر |
تُسمي هذه الخصائص بخصائص (أو بديهيات) الأعداد الصحيحة وهي افتراضات تم افتراضها في الماضي، وفي وقت لاحق تطورت رياضياً مع بناء مفهوم الأعداد الصحيحة.
الزوجية والفردية
الأعداد الصحيحة إما أن تكون زوجية أو فردية. على سبيل المثال الأعداد الصحيحة 2, 42 و 42- هي عبارة عن أعداد زوجية، والأعداد الصحيحة 1, 17 و 175- هي عبارة عن أعداد فردية. فإذا كان العدد الصحيح يقبل القسمة علـى 2 فهو عدد زوجي أما إذا كان لا يقبل القسمة علـى 2 فهو عدد فردي. على سبيل المثال العدد 6 هو عدد صحيح زوجي لانه يقبل القسمة علـى 2 أي يمكن تقسيمه علـى 2 دون باقي. أما العدد 7 فهو عدد صحيح فردي لانه لا يقبل القسمة علـى 2 أي لا يمكن تقسيمه علـى 2 دون باقي.
طريقة أخرى للتعبير عن ذلك:
العدد الزوجي هو عدد صحيح يمكن كتابته في الصيغة
$$2\cdot k$$
حيث أن k هو عدد صحيح. على سبيل المثال يمكن وضع \(k=3\) والحصول على
$$2\cdot k= 2\cdot 3= 6$$
وهو عدد زوجي
العدد الفردي هو عدد صحيح يمكن كتابته في الصيغة
$$2\cdot k+1$$
حيث أن k هو عدد صحيح. على سبيل المثال يمكن وضع \(k=5\) والحصول على
$$2\cdot k+1=2\cdot 5+1=10+1=11$$
وهو عدد فردي.
وهكذا بوضع قيّم مختلفة من الأعداد الصحيحة بدلا من k يمكننا الحصول على جميع الأعداد الفردية والزوجية.
الأعداد النسبية
الأعداد النسبية هي جميع الأعداد الصحيحة والأعداد الكسرية التي يمكن كتابتها في صورة:
$$\frac{a}{b},\, b\neq 0$$
حيث أن a و b أعداد صحيحة.
أمثلة على الأعداد النسبية:
$$\\0, \;3, \;-17, \;\frac{13}{7}, \;2,4, \;-0,6$$
يُرمز لمجموعة الأعداد النسبية بالحرف \(\mathbb{Q}\).
\(\mathbb{Q}\) = \(\}\)كل الأعداد في صورة \(\frac{a}{b}\), حيث أن \(\;a\) و \(\;b\) أعداد صحيحة و \(\;b \neq 0\)\(\{\)
الأعداد الغير النسبية
جميع الأعداد التي لا يمكن كتابتها في صورة نسبة بين عددين صحيحين هي أعداد غير نسبية.
تشمل أمثلة الأعداد الغير النسبية كل من \(\sqrt2\) (الجذر التربيعي للعدد الصحيح الغير مُربع)، \(\pi\) (pi) والعدد e (العدد e سنقابله لاحقا في احدى الدورات "الكورسات" الدراسية القادمة).
الأعداد الحقيقية
الأعداد النسبية والأعداد الغير النسبية جميعها معا هي التي تُشكل الأعداد الحقيقية. يُرمز لمجموعة الأعداد الحقيقية بالحرف \(\mathbb{R}\). جميع الأعداد التي سنقابلها في هذه الدورة (الكورس) هي عبارة عن أعداد حقيقية.
مجموعات الأعداد معاً
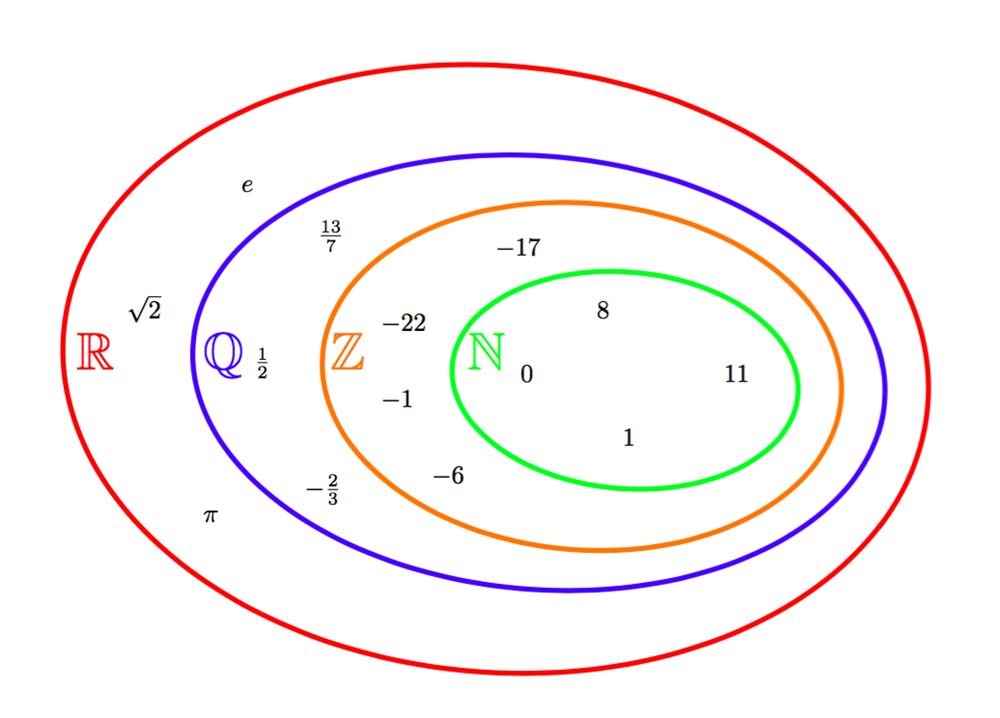
كل مجموعة من هذه المجموعات تصف أنواع مختلفة من الأعداد. ترتبط هذه المجموعات وأعدادها وفقا لما يلي:
الأعداد الطبيعية \(\mathbb{N}\) تدخل ضِمن مجموعة الأعداد الصحيحة \(\mathbb{Z}\) التي بدورها تدخل ضِمن مجموعة الأعداد النسبية \(\mathbb{Q}\) والتي هي أيضا بدورها تدخل ضِمن مجموعة الأعداد الحقيقية \(\mathbb{R}\).
فيديوهات الدرس (بالسويدية)
في هذا الفيديو نستعرض أنواع مختلفه من الأعداد.
في هذا الفيديو نستعرض الأعداد النسبية ومفهوم المضاعفة و الإختصار.
في هذا الفيديو سنشرح الفرق بين الأعداد النسبية والغير نسبية.
