أنظمة الأعداد

في الأقسام السابقة افترضنا أنه يمكن تلقائيا تفسير أي عدد من الأعداد مثل 42. ولكن إذا نظرنا للموضوع بصورة أوسع سيتضح أنه الى يومنا هذا وعلى مدار التاريخ توجد العديد من أنظمة الأعداد المختلفة المُستخدمة في تحديد قيّم الأعداد بإستخدام ما يُعرف بنظام المواقع (أي مواقع الأرقام التي يتكون منها العدد). في هذا القسم سنناقش نظام المواقع وبعض أنظمة الأعداد الأكثر شيوعا التي تتبع نظام المواقع.

نظام المواقع

مفهوم أنظمة الأعداد المألوفه لدينا مبني على ما يُسمى بنظام المواقع. مواقع الأرقام في أي عدد هي التي تحدد قيمة الرقم كما هي التي تحدد قيمة العدد. كل رقم له قيمة مختلفه بناءاً على موقعه في العدد. الرقم الذي سيكون في أقصي يسار العدد هو الأكبر قيمه بينما الرقم الذي سيكون في أقصى اليمين هو الأقل قيمه.

نظام الأعداد المستخدم في أغلب الحسابات العاديه هو النظام العشري وهو يتكون من خانات صحيحة وخانات عشرية.

نظام الأعداد العشري

النظام العشري هو نظام الأعداد التي نستخدمها في حياتنا اليومية. هذا النظام أساسه 10 ويتكون من عشرة أرقام: (0, 1, 2, 3, 4, 5, 6, 7, 8 و 9). في أي عدد من الأعداد كل رقم تختلف قيمته حسب موقعه في العدد. يمكننا توضيح ذلك بدراسة مواقع أرقام العدد العشري 528,149 كما يلي:

 

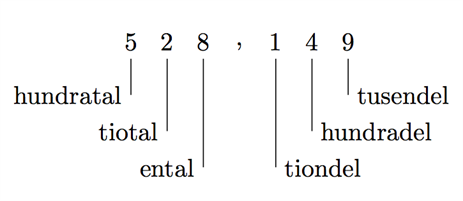
اللغة السويدية	اللغة العربية
hundratal	مئات
tiotal	عشرات
ental	آحاد
tiondel	جزء من عشرة (أعشار)
hundradel	جزء من مائة
tusendel	جزء من ألف

 نلاحظ أن قيمة الرقم 5 في هذا الموقع هي 500 لأنه في موقع أو خانة المئات, قيمة الرقم 2 هي 20 لأنه في خانة العشرات, وهكذا. بالتالي الموقع هو الذي يحدد القيمة التي يمثلها الرقم. فإذا تحركنا خطوة ناحية اليسار نضرب الرقم فـي 10 أما إذا تحركنا خظوة ناحية اليمين نقسم علـى 10 وهكذا كل خطوة تُغيّر قيمة الرقم بالعامل 10.

فإذا فكرنا في العدد 42, ما معناه في الواقع؟ وفقا لنظام الأعداد المعروف بنظام الأعداد العشري، فهو يعني أربع عشرات (40) وإثنان (واحد زائد واحد أي وحدتين)، ويمكن أيضا كتابته على النحو التالي:

$$42=40+2=4\cdot 10^{1}+2\cdot 10^{0}$$

وهذه طريقة أخرى لتوضيح قيّم الأرقام في مواقعها المختلفه.

نظام الأعداد الثنائي

هناك أنظمة أعداد أخرى تُبنى من عدد من الأرقام غير النظام العشري. مثال على ذلك النظام الثنائي. ويُسمى هذا النظام بالنظام الثنائي لأنه يحتوي على رقمين فقط وهما الصفر والواحد. عادة ما يُستخدم النظام الثنائي في الإلكترونيات الرقمية كالحواسب الآلية (أجهزة الكمبيوتر). نظام الأعداد الثنائي أيضا تحكمه مواقع الأرقام.

في عالم الأعداد العشرية تزيد أو تنقص قيمة الرقم بالعامل 10 حسب موقعه في العدد. أما في عالم الأعداد الثنائية تزيد أو تنقص القيمة بالعامل 2.

مثلا إذا كان لدينا العدد 10011 فهو مبني من رقمين (الصفر والواحد وهما متضمنان في النظامين العشري والثنائي) فإذا كان هذا العدد مكتوب وفقا لنظام الأعداد العشري فهذا يعني أن:

$$10011=1\cdot 10^{4}+0\cdot 10^{3}+0\cdot 10^{2}+1\cdot 10^{1}+1\cdot 10^{0} $$

ويمكن أيضا كتابته كما يلي:

$$\begin{align}10011 & =10000+0+0+10+1=\\ & =10000+10+1=\\ & =10000+11 \end{align}$$

وهذا يعطينا العدد 10011 نفسه كعدد نظام عشري.

أما إذا كان هذا العدد 10011 مكتوب وفقا لنظام الأعداد الثنائي فهذا يعني أن:

$$\begin{align}10011 & =1\cdot 2^{4}+0\cdot 2^{3}+0\cdot 2^{2}+1\cdot 2^{1}+1\cdot 2^{0}=\\ & =16+0+0+2+1=19 \end{align}$$

بمعني أن عدد النظام الثنائي 10011 يعادل 19 بالنظام العشري, ونلاحظ أنه أصبح يتكون من الرقمين (1 و 9) والــ 9 هي من أرقام النظام العشري وليس من أرقام النظام الثنائي.

كما نعلم أن أي عدد يمكن كتابته في صورة مجموعة من الحدود حسب قيمته. كل حد من هذه الحدود عبارة عن حاصل ضرب (الرقم) × (أساس مرفوع لقوة). هذا الأساس هو عبارة عن عدد أرقام النظام. في حالة النظام العشري الأساس هو 10 لأنه يتكون من عشرة أرقام (0, 1, 2, …, 9) وفي حالة النظام الثنائي الأساس هو 2 لأنه يتكون من رقمين (0 و 1). أما القوة فهي عبارة عن عدد أصفار الرقم وهي تعتمد على موقع الرقم (للآحاد القوة صفر، للعشرات القوة واحد، للمئات القوة 2 وهكذا). لتحويل أي عدد من النظام الثنائي إلى النظام العشري نكتب العدد كمجموع قوي العدد 2 ثم نجمع قيّم هذه الحدود كما في المثال أعلاه، حيث توصلنا الى أن 10011 بالنظام الثنائي يساوي 19 بالنظام العشري.

للتمييز بين أنظمة الأعداد المختلفة عادة ما يُكتب إسم النظام (عددا) في أسفل العدد على الجانب الأيمن. على سبيل المثال إذا كان العدد بنظام الأعداد العشري يُكتب كما يلي

$$10011_{10}$$

أما إذا كان العدد بنظام الأعداد الثنائي يُكتب كما يلي

$$10011_{2}$$

أنظمة أعداد ذات أساسات مختلفة

هناك أنظمة أعداد أخرى مختلفة تُبنى من عدد آخر من الأرقام غير نظام الأعداد الثنائي ونظام الأعداد العشري. كل نظام أعداد له أساس، هذا الأساس هو الذي يحدد عدد الأرقام التي يمكن استخدامها في نظام الأعداد. إذا أخذنا نظام الأعداد ذي الأساس 5, بالتالي سنستخدم خمسة أرقام فقط (0, 1, 2, 3 و 4). تماما كما في نظام الأعداد العشري (الذي أساسه 10) ونظام الأعداد الثنائي (الذي أساسه 2)، وموقع الرقم في العدد هو الذي يحدد قيمته. وكل هذه الأنظمة ذات الأساسات المختلفه تحكمها مواقع الأرقام.

مثلا إذا كان لدينا العدد 343 مكتوب في نظام الأعداد ذي الأساس 5, يمكننا كتابته كـ 343₅ لنوضيح أننا نعني نظام الأعداد ذي الأساس 5. إذا أردنا يمكننا إعادة كتابة هذا العدد بنظام الأعداد ذي الأساس 10 (نظام الأعداد العشري) كما يلي:

$$\begin{align} 343_5 &=(3\cdot 5^2+4\cdot 5^1+3\cdot 5^0)_{10}=\\ &=(3\cdot 25+4\cdot 5+3\cdot 1)_{10}=\\ &=98_{10} \end{align}$$

بالتالي أي عدد مكتوب في نظام الأعداد ذي الأساس خمسه (نظام الأعداد الخُماسي) أرقامه من اليمين الى اليسار عبارة عن حدود عواملها: واحد, خمسة, خمسة وعشرون, مائة وخمسة وعشرون وهكذا.

نظام الأعداد الروماني

في الإمبراطورية الرومانية في قديم الزمان لم يكن نظام الأعداد مثل نظام الأعداد المُستخدم اليوم. فبدلا من ذلك كانوا يستخدمون العلامات التالية:

الرقم الروماني	I	V	X	L	C	D	M
الرقم العشري المقابل	1	5	10	50	100	500	1000

يتم تفسير العدد في نظام الأعداد الروماني وفقا للقواعد التالية:

إذا كان هناك رقمين متشابهين بجوار بعضهما البعض يُجمعان معا، على سبيل المثال (2 = II = 1 + 1). إذا كان هناك رقم أصغر وبعده رقم أكبر فمن ثم يُطرح الرقم الأصغر من الرقم الأكبر مثل (IV = 5 - 1 = 4) إذا كان هناك رقم أصغر وقبله رقم أكبر فمن ثم يجمع الرقم الأصغر مع الرقم الأكبر, مثل

(VI = 5 + 1 = 6)

باستخدام هذه الأرقام الرومانية يمكننا التعبير عن جميع الأعداد، ولكن إجراء عمليات حسابية مختلفة سيصبح أمرا معقدا جدا. مثلا جمع العدد MCMXCIX مع نفسه أمر صعب ولكنه ممكن. أما محاولة ضرب العدد MCMXCIX ستكون أصعب.

تستخدم الأرقام الرومانية في الوقت الحاضر بشكل كبير في الساعات وكتابة السنوات. كما تُستخدم أيضا لترقيم القوائم, على سبيل المثال:

I. استيقاظ
II. نهوض
III. ارتداء الملابس
IV. تناول الإفطار

كيف يمكننا التعبير عن العدد 437 (المكتوب وفقا لنظام الأعداد العشري) بنظام الأعداد الروماني؟

نبدأ بكتابة العدد كمجموع أعداد آخرى، ومنها يمكننا بسهولة إعادة كتابته وفقا لنظام الأعداد الروماني:

$$437=400+30+7$$

الآن يمكن إعادة كتابة كل حد من حدود هذا المجموع وتحويلها الى نظام الأعداد الروماني وفقا للقواعد والجدول أعلاه

$$\begin{align} 437 & =400+30+7=\\ & =(-100+500)+(10+10+10)+(5+1+1)=\\ & =CDXXXVII \end{align}$$

---

فيديو الدرس (بالسويدية)

في هذا الفيديو سنشرح مفهوم نظام الأعداد الثنائي.

هنا سنشرح كيف يمكننا تحويل الأعداد من النظام العشري إلى النظام الثنائي.

فيديو آخر عن مفهوم نظام الأعداد.

 

آلة حاسبة كوسيلة مساعدة

في هذا التمرين تم استخدام الآلة الحاسبة البيانية (Casio FX-CG20).
شاهد نفس التمرين على الآلة الحاسبة البيانية (Casio FX-9750GII).

الآلات الحاسبة البيانية من الماركات الأخى لديها نفس الوظائف تقريبا.