نظام الإحداثيات و رسم الدوال
في القسم السابق تعلمنا أن الدالة هي علاقة أو قاعدة تعني أن قيمة متغير معين تعتمد على قيمة متغير آخر أو أكثر من متغير.
في هذا القسم سندرس كيف يمكننا استخدام نظام الإحداثيات والرسوم البيانية لعرض كيفية التغير في قِيّم الدالة. باستخدام نظام الإحداثيات والرسوم البيانية سيكون من السهل أن نفهم كيفية عمل الدوال.
نظام الإحداثيات
في السابق استخدمنا خط الأعداد لتوضيح ارتباط الأعداد المختلفة ببعضها البعض.
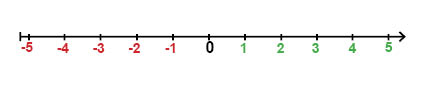
يتكون نظام الإحداثيات من خطين عددييّن: خط أعداد أفقي وخط أعداد رأسي. هاذان الخطان العدديان يلتقيان في نقطة تسمى نقطة الأصل، وهي نقطة الصفر لكلا الخطان العدديان. وعادة ما يُسمى خطي الأعداد في نظام الإحداثيات بمحوري الإحداثيات.
يكون نظام الإحداثيات كما في الشكل أدناه:
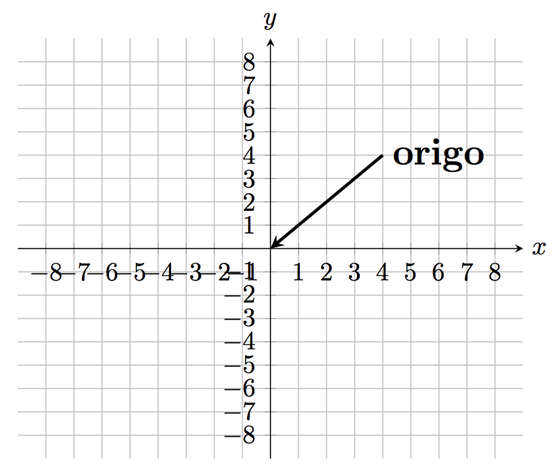
كلمة origo الموضحة في الرسم تعني نقطة الأصل.
في نظام الإحداثيات عادة ما يُسمى خط الأعداد الأفقي بمحور x وخط الأعداد الرأسي بمحور y.
في نظام إحداثيات يمكننا تحديد نقاط مختلفة. في نظام الإحداثيات الشائع تُكتب النقاط باستخدام الأعداد الزوجية، وفيها يُسمي العدد الأول بالقيمة الإحداثية لــ x, والعدد الثاني بالقيمة الإحداثية لــ y.
إذا أردنا على سبيل المثال تحديد نقطة فيها قيمة x تساوي 2 وقيمة y تساوي 3, ففي هذه الحالة نكتب النقطة كما يلي: (3, 2). القيمة الأولى في هاذين القوسين هي 2 وهي قيمة x, والقيمة الثانية هي 3 وهي قيمة y.
يمكننا وضع أي علامة على النقطة (3, 2) في نظام الإحداثيات كما يلي:
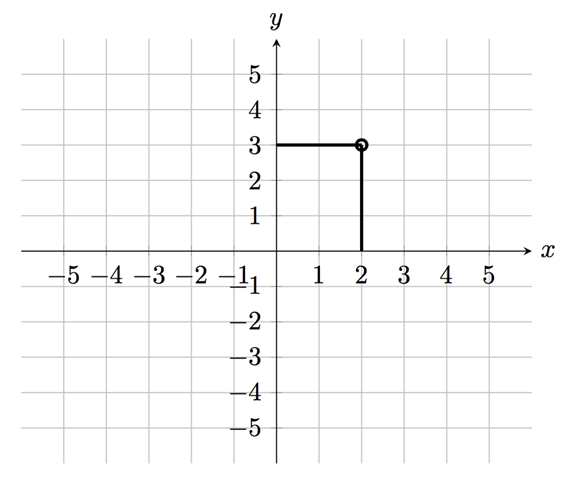
في نظام الإحداثيات يمكن أن نلاحظ أن القيمة الأولى في زوج الأعداد (3, 2) هي القيمة (2) نفسها التي تقع على المحور الأفقي (محور السينات). أيضا يمكن أن نلاحظ أن القيمة الثانية في زوج الأعداد هي القيمة (3) نفسها التي تقع على المحور الرأسي (محور الصادات). وهكذا يمكننا بدقة تعيين النقاط التي تقع على نظام الإحداثيات باستخدام زوج الأعداد (x, y).
عند النقطة التي تُسمى نقطة الأصل تكون قيمة كل من x و y مساوية للصفر لذلك تُكتب (0, 0).
حدد النقاط (4, 1), (1, -2), (-1, -3) و (-2, 2) على نظام إحداثيات
نبدأ بالنقطة الأولى (4, 1). القيمة الأولى (من زوج الأعداد) هي قيمة x على المحور الأفقي والقيمة الثانية هي قيمة y على المحور الرأسي.
لذلك سنحدد موقع هذه النقطة عند التقاء الخط المتقطع الممتد من النقطة 1 على محور x مع الخط المتقطع الممتد من النقطة 4 على محور y. بهذه الطريقة يمكننا توضيح هذه النقطة بالضبط على نظام الإحداثيات, أنظر الشكل أدناه:
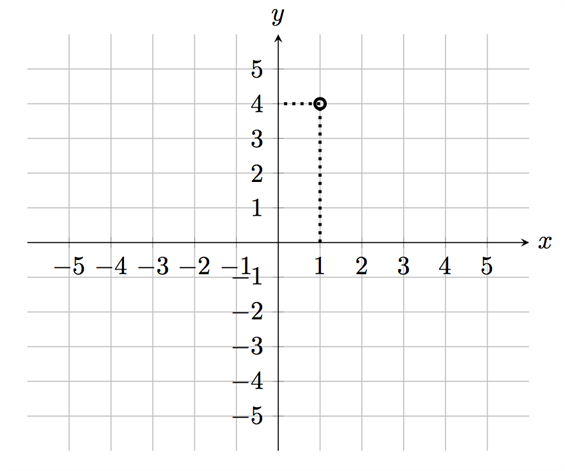
بنفس الطريقة يمكننا تحديد النقاط (1, -2)، (-1, -3) و (-2, 2) على نظام الإحداثيات. بحيث نحدد كل نقطة من هذه النقاط عند التقاء الخط الممتد من قيمة x على المحور الأفقي والخط الممتد من قيمة y على المحور الرأسي.
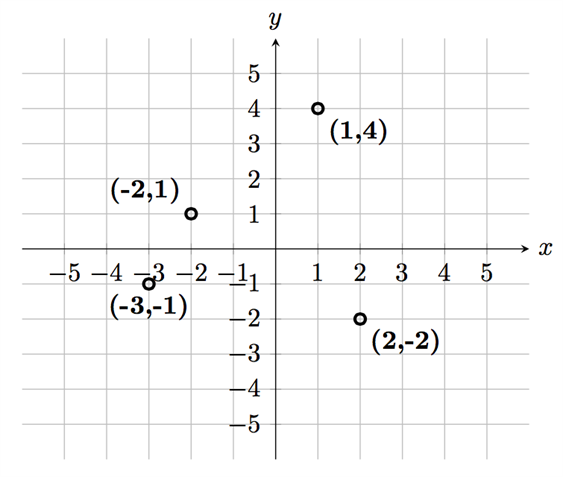
رسم الدوال
يمكننا استخدام نظام الإحداثيات لتوضيح كيفية اعتماد قيمة الدالة على قيمة المتغير. بحيث يتم تحديد قيمة الدالة على محور y والمتغير الذي تعتمد عليه قيمة الدالة على محور x.
في قسم الدوال لدينا مثال عن أجر سارة بالساعة مقابل عملها الإضافي. يعتمد إجمالي أجرها على عدد الساعات التي عملتها وفقا للدالة التالية:
\(x80=y(x)\)
y هو إجمالي أجر سارة بالكرونة و x هو عدد الساعات التي عملتها.
يمكننا رسم هذه العلاقة على نظام الإحداثيات كما يلي:
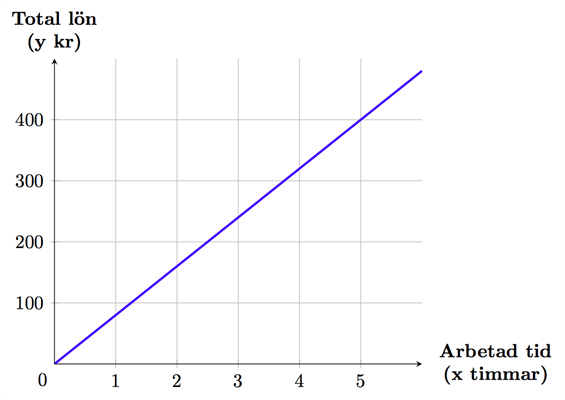
معاني الكلمات السويدية على الرسم:
| اللغة السويدية | اللغة العربية |
| (Arbetad tid (\(x\) timmar | ساعات العمل (\(x\) ساعة) |
| (Total lön (\(y\) kr |
الراتب الكلي (\(y\) كرونة) |
عندما نرسم مخطط بياني على نظام الإحداثيات نحصل دائما على منحنى أو خط بدلا من عِدة نقاط. وفي الحقيقة يمكننا الحصول على أي نقطة على مخطط الدالة باختيار قِيمة معينة للمتغير x وحساب قيم الدالة y التي تقابلها في نظام الإحداثيات.
يمكن قراءة أجر سارة على طول هذا الخط حسب عدد الساعات التي عملتها. فإذا عملت سارة على سبيل المثال لمدة ساعة واحدة فيمكننا قراءة أجرها عند النقطة (80, 1)، وهي النقطة التي نجد أنفسنا عندها إذا قرأنا 1 على المحور الأفقي. نلاحظ أن ارتفاع هذه النقطة من المحور الأفقي (محور x) أقل من 100 على محور y, أي أن قيمة y المقابلة هي \(80 = y\). يمكن تفسير هذا بأن سارة تحصل على 80 كرونة (قيمة y) مقابل عملها لمدة ساعة واحدة (قيمة x).
أقل أجر لسارة هو 0 كرونة وهذا في حالة عملها لمدة 0 ساعة وهو أقل زمن (أي في حالة عدم عملها)، لهذا نحتاج الى رسم جميع القيّم على امتداد محوري الإحداثيات وأقل قيمة ستكون 0 وهذا يتمثل في نقطة الأصل (0, 0).
في الحقيقة أجر سارة عبارة عن قيمة تناسبية. والتناسب يعني أن مخطط الدالة عبارة عن خط مستقيم يمر بنقطة الأصل.
عندما يكون لدينا دالة معروفة، على سبيل المثال
\( x80=y(x) \)
فمن ثم يمكننا رسمها لقراءة قيّم الدالة المختلفة حسب قيمة المتغير الذي تعتمد عليه الدالة. و غالبا ما يكون من السهل فهم كيفية عمل الدالة إذا نظرنا إلى شكلها في نظام إحداثيات.
في بعض الأحيان يكون لدينا نقاط معينة ونريد معرفة الدالة الصحيحة لهذه النقاط.
ارتفاع القذيفة من الأرض
إذا رمزنا لارتفاع قذيفة عن الأرض بـ y (بالمتر) ورمزنا إلى الوقت المنقضي منذ قذفها من المدفع بـ t (بالثانية).
ويمكن وصف ارتفاع القذيفة عن الأرض بالدالة التالية:
\( 1+t5+{t}^{2}0,7-=y(t)\)
إذا رسمنا هذه الدالة في نظام إحداثيات فسنحصل على المنحنى التالي:
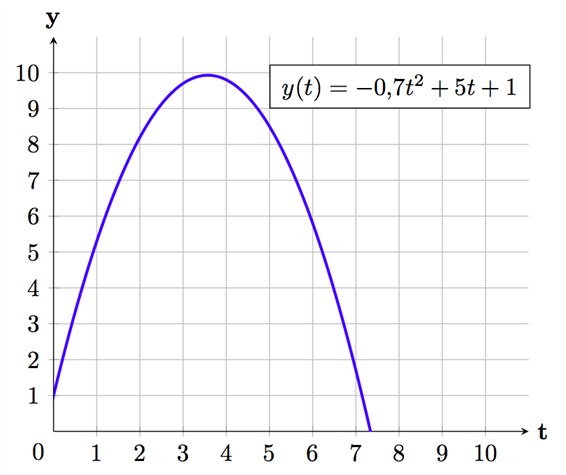
استخدم هذا الرسم لقراءة ارتفاع القذيفة عن الأرض بعد فترة زمني قدرها:
a) \(1\) ثانية
b) \(4\) ثوان
الحل:
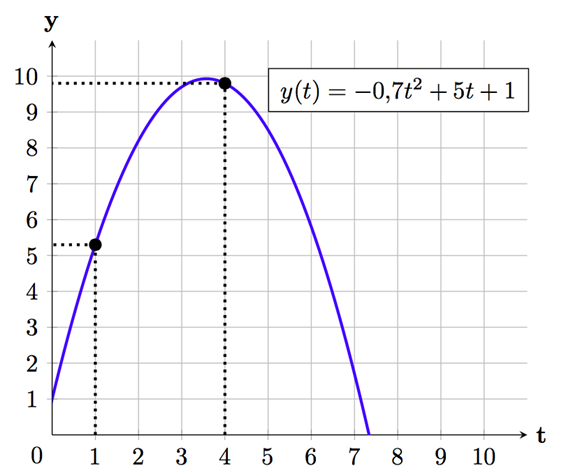
a)
لقراءة ارتفاع القذيفة بعد 1 ثانية سننظر أولا على المحور الأفقي الذي يوضح الوقت (بالثواني) ونبحث عن القيمة \(1 = t\).
ثم نتخيل خط مستقيم يصل بين المحور الأفقي عند القيمة \(1 = t\) والمنحنى. سيتقاطع هذا الخط مع المنحنى عند نقطة معينة, عند هذه النقطة يمكننا قراءة ارتفاع القذيفة عن الأرض بعد 1 ثانية.
يمكننا قراءة أن ارتفاع القذيفة عن الأرض بعد واحد ثانية سيكون 5,3 متر تقريبا.
b)
بنفس الطريقة بالنسبة للأربع ثواني كما فعلنا في حالة الواحد ثانية.
من الرسم نلاحظ أن القذيفة بعد 4 ثوان ستكون على ارتفاع أعلى من ارتفاعها بعد 1 ثانية. فإذا قرأنا ارتفاع القذيفة عند الأربع ثواني سيكون حوالي 9,8 متر فوق سطح الأرض.
بهذه الطريقة يمكننا أيضا قراءة ارتفاع القذيفة فوق سطح الأرض لكل الأوقات الأخرى. على سبيل المثال هل يمكنك أن تعرف متى ستقع القذيفة على الأرض، أي متى يكون الارتفاع 0 متر؟
فيديوهات الدرس (باللغة السويدية)
مفهوم نظام الإحداثيات (المحاور) وكيفية استخدامه.
الدوال الخطية والخط المستقيم.
مفهوم ميل الخط الموجب والسالب على نظام الإحداثيات (المحاور).
