نظرية فيثاغورس
في الصف الثامن تعلمنا المثلثات بما في ذلك المثلثات القائمة الزاوية، وهي المثلثات التي لها زاوية قائمة مقدارها °90.
أيضا تعلمنا حساب القوى و الجذور التربيعية في الأقسام السابقة في الصف التاسع.
في هذا القسم سنتعرف على نظرية فيثاغورس، وهي نظرية رياضية مفيدة جدا تتعلق بالمثلثات القائمة الزاوية. إستخدام نظرية فيثاغورس يتضمن عملية حساب كل من القوى (الأُسُس) والجذور التربيعية، كما تعلمنا في أحد الأبواب السابقة.
نظرية فيثاغورس
المثلث القائم الزاوية هو مثلث به زاوية قائمة مقدارها °90.
هنالك أسماء خاصة عادة ما تستخدم لتسمية أضلاع المثلث القائم الزاوية. يسمى الضلعين المتقابليّن عند عند الزاوية القائمة بالضلعين القائميّن بينما يسمى الضلع الثالث بالوَتَر.
في الصورة التالية الضلع c هو وَتَر المثلث القائم الزاوية والضلعين a و b هما ضلعي المثلث القائميّن.
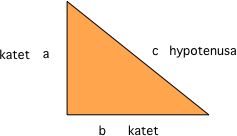
تَنص نظرية فيثاغورس على أن أي مثلث قائم الزاوية ترتبط أضلاعه بالعلاقة التالية:
\( {c}^{2}={b}^{2}+{a}^{2}\)
أي أن مجموع مُربعي الضلعين القائميّن يساوي مربع الوَتَر. حيث أن a و b هما أطوال الضلعيّن القائميّن و c هو طول الوَتَر.
أُخذ اسم نظرية فيثاغورس من اسم عالم الرياضيات اليوناني فيثاغورس الذي عاش منذ حوالي 2500 عام في الماضي. علاوة على ذلك أُستخدمت هذه النظرية المهمة في السابق أكثر مما هو مدرج في بابل.
الآن سندرس كيفية استخدام نظرية فيثاغورث وذلك من خلال دراسة مثلث قائم الزاوية أطوال أضلاعه الثلاثة معلومة.
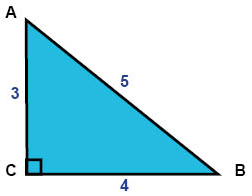
في المثلث القائم الزاوية أعلاه زاوية الرأس C هي زاوية قائمة. وهذا يعني أن الضلعين اللذيّن طولهما 3 و 4 وحدة طولية هما ضلعي المثلث القائميّن. أما الضلع الثالث الذي طوله 5 هو وَتَر المثلث.
وفقا لنظرية فيثاغورس ستنطبق العلاقة التالية بين أضلاع المثلث:
\( {5}^{2}={4}^{2}+{3}^{2}\)
لنتحقق مما إذا كان هاذين الطرفين متساويين أم لا، وذلك بتبسيط الطرفين الأيمن والأيسر كل على حدة.
الطرف الأيمن =
\(={4}^{2}+{3}^{2}\)
\(=4\cdot 4+3\cdot 3=\)
\(=16+9=\)
\(25=\)
الطرف الأيسر =
\(={5}^{2}\)
\(=5\cdot 5=\)
\(25=\)
الطرف الأيمن يساوي الطرف الأيسر. إذن نظرية فيثاغورس صالحة لهذا المثلث.
في حالة عدم تساوي الطرفين الأيمن والأيسر، فهذا يعني أن طول أحد أضلاع المثلث خطأ أو قد لا يكون المثلث قائم الزاوية. عليه يمكننا استخدام نظرية فيثاغورس لتحديد ما إذا كان المثلث قائم الزاوية أم لا.
احسب باستخدام نظرية فيثاغورس
إذا علمنا طول ضلعين من أضلاع مثلث قائم الزاوية يمكننا معرفة طول الضلع الثالث باستخدام نظرية فيثاغورس.
من المهم جدا معرفة وتحديد الضلعين القائمين (ضلعي الزاوية القائمة) ووَتَر المثلث عند استخدام نظرية فيثاغورس.
الآن سنستخدم نظرية فيثاغورس في بعض المواقف الشائعة التي يمكن أن تحدث.
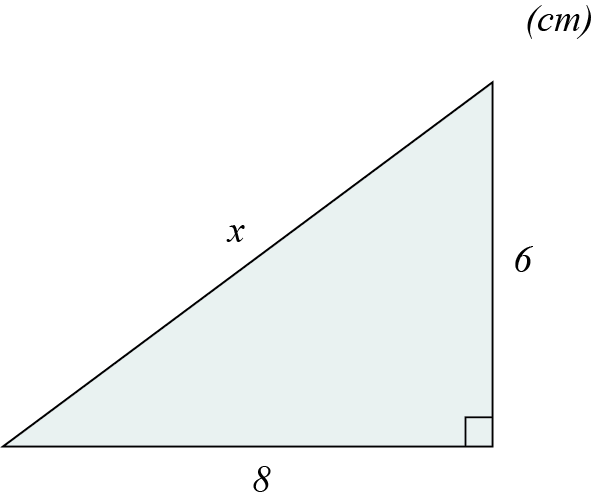
احسب طول الضلع \(x\) باستخدام نظرية فيثاغورس
الحل:
من الشكل نلاحظ أن الضلعين اللذين طولهما 6 و 8 سم يلتقيان معا عند الزاوية القائمة ما يعني أنهما يمثلان ضلعي المثلث القائميّن. بالتالي يجب أن يكون الضلع الذي طوله \(x\) هو وَتَر المثلث.
بما أننا حددنا ضلعي المثلث القائميّن ووَتَره يمكننا استخدام نظرية فيثاغورس لحساب قيمة \(x\):
\( {x}^{2}={8}^{2}+{6}^{2}\)
\({x}^{2}=64+36 \)
\({x}^{2}=100\)
وفقا لهذه المعادلة سيكون حاصل ضرب \(x\) في نفسها يساوي 100. لحل المعادلة سنحسب الجذر التربيعي لـ 100 وهو ما يعطينا العدد الذي إذا ضربناه في نفسه سيعطي 100.
\( 10=\sqrt{100}=x\)
إذن يجب أن يكون طول الوَتَر 10 سم.
احسب طول الضلع \(x\) باستخدام نظرية فيثاغورس

الحل:
نبدأ بتحديد الزاوية القائمة وهي التي توجد في شمال أسفل الشكل. الضلعان اللذان طولهما \(x\) متر و 12 متر يلتقيان عند الزاوية القائمة، لذا هاذين الضلعين هما الضلعين القائميّن. لهذا لابد أن يكون الضلع الذي طوله 13 متر هو الوَتَر.
بما أننا حددنا ضلعي المثلث القائميّن ووَتَره يمكننا كتابة العلاقة بين أطوال أضلاع المثلث باستخدام نظرية فيثاغورس:
\( {13}^{2}={12}^{2}+{x}^{2}\)
لإيجاد قيمة \(x\) نبدأ بتبسيط طرفي هذه المعادلة:
\({13}^{2}={12}^{2}+{x}^{2}\)
\(169=144+{x}^{2}\)
\({\color{Red} \,144\,-}169={\color{Red} \,144\,-}144+{x}^{2}\)
\(25={x}^{2}\)
وفقا لهذه المعادلة سيكون حاصل ضرب \(x\) في نفسها يساوي 25. لذا \(x\) يجب أن تساوي الجذر التربيعي لــ 25.
\( 5=\sqrt{25}=x\)
إذن يجب أن يكون طول الضلع \(x\) 5 أمتار.
فيديوهات الدرس (باللغة السويدية)
مفهوم نظرية فيثاغورس.
هنا نواصل في مفهوم نظرية فيثاغورس.
