الدوال
سابقا تعلمنا كيفية كتابة التعبيرات التي بها متغيرات كما تعلمنا كيفية كتابة المعادلة في الصف الثامن.
في هذا القسم سنتعلم الدوال. الدوال هي علاقات أو قواعد تربط بين المتغيرات وتنُص على أنه إذا كان لدينا دالة بين متغيرين وعلمنا قيمة أحدهما فمن ثم يمكننا ايجاد قيمة المتغير الآخر. تُستخدم الدوال بشكل كبير في الرياضيات لوصف مواقف مختلفة، لذلك من المهم فهم كيفية عملها.
ما هي الدالة؟
هناك حالات عديدة يمكننا أن نقول فيها أن قيمة متغير معين تعتمد على قيمة متغير آخر.
على سبيل المثال قد يعتمد إجمالي السعر الذي ستدفعه للتفاح الذي يُباع بسعر 15 كرونة/كجم، على إجمالي وزن التفاح الذي ستشتريه. يمكن أن نرمز لوزن التفاح بالمتغير x والسعر الذي يجب أن ندفعه بالمتغير y.
في هذه الحالة نقول أن السعر y الذي يجب أن ندفعه للتفاح هو دالة في وزن التفاح x (أي y دالة في x).
ويمكننا كتابة هذه العلاقة على النحو التالي:
\(x15=y\)
بشكل عام، الدالة هي علاقة تعني أن قيمة متغير معين تعتمد على قيمة متغير آخر أو أكثر من متغير. لدينا في المثال أعلاه تعتمد قيمة المتغير y على قيمة المتغير x, وفي هذه الحالة قيمة المتغير y أكبر من قيمة المتغير x بــ 15 مرة.
يمكن أن ننظر الى الدالة على أنها آلة تُدخل فيها قيمة متغير معينة في أحد نهايتيها وتحصل على قيمة معينة لمتغير آخر من النهاية الأخرى للآلة. الدالة هي التي تحدد ما تفعله "الآلة" مع قيمة المتغير الذي تتلقاه.
أنظر الى الدالة أدناه التي توضح أن قيمة المتغير y تعتمد على قيمة المتغير x وفقا للقاعدة التالية:
\(2+x=y\)
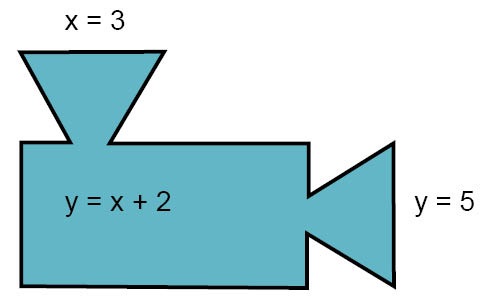
هذه الدالة (القاعدة) تنُص على أن قيمة y ستكون أكبر من قيمة x بــ 2.
إذا وضعنا على سبيل المثال قيمة المتغير \(x = 3\) في الدالة, بالتالي استبدلنا x بالعدد 3 في تعبير الدالة, ومن ثم ستكون قيمة المتغير y على النحو التالي:
\(=2+x=y\)
\(=2+3=\)
\(5=\)
ولكي تصبح أكثر وضوحا عندما يكون لدينا دالة، عادة ما نكتب أن قيمة المتغير y تعتمد على قيمة المتغير x, على النحو التالي:
\(y(x)\)
من مثال "دالة الآلة" أعلاه يمكن أن نكتب الدالة كما يلي:
\(2+x=y(x)\)
إذا أردنا حساب قيمة المتغير y عندما تكون قيمة المتغير x هي 3, فسنكتب كما يلي:
\(5=2+3=y(3)\)
أحد الخصائص الهامة للدوال هي أن كل قيمة نضعها في دالة معينة تعطي دائما نفس القيمة. وهذا يعني أن الدوال قابلة للتنبؤ. العلاقة التي لا تحتوي على هذه الخاصية لا يمكن أن تكون دالة.
أمثلة على الدوال
توجد الدوال في العديد من السياقات المختلفة. وهنا بعض الأمثلة على الدوال.
الراتب الذي تحصل عليه سارة في عملها الإضافي حيث تتقاضى أجرها بالساعة يُعتبر دالة في عدد الساعات التي تعملها.
يمكن اعتبار أن محيط الدائرة دالة في نصف قطر الدائرة.
عندما يكون سعر التفاح بالكيلو فسيكون سعر البيع دالة في وزن التفاح.
ارتفاع قذيفة المدفع عن الأرض عبارة عن دالة في الزمن المنقضي منذ لحظة قذفها من المدفع.
احسب باستخدام الدوال
سنقوم الآن بإجراء العمليات الحسابية باستخدام العديد من الدوال المختلفة.
أجر سارة في الساعة
تعمل سارة عمل إضافي وتحصل على 80 كرونة/ساعة.
يمكن أن نرمز إلى الراتب الذي تحصل عليه سارة بـ y كرونة ونرمز إلى عدد الساعات التي تعملها بـ x ساعة.
يمكن أن ننظر الى أجر سارة y كرونة كدالة في عدد الساعات التي تعملها x, وفقا لهذه الدالة:
\( x80=y(x)\) كرونة
أحسب \(y(10)\) ثم فسّر ماذا يعني التعبير.
الحل:
لحساب \(y(10)\) سندخل 10 في مكان x في الدالة أي نعوض x بــ 10:
\( 10\cdot 80=y(10)\) كرونة = 800 كرونة
يمكن تفسير هذا بأن سارة عملت لمدة 10 ساعات وحصلت على 800 كرونة كأجر لهذه الفترة الزمنية.
ارتفاع قذيفة من الأرض
نرمز الى ارتفاع القذيفة من الأرض (بالمتر) بالمتغير y. ونرمز إلى طول المدة الزمنية (بالثواني) منذ إطلاق المدفع للنار بالمتغير t.
يمكننا حساب ارتفاع قذيفة المدفع عن سطح الأرض باستخدام هذه الدالة:
\( 1+t5+{t}^{2}0,7-=y(t)\)
احسب \(y(2)\) وفسّر معني التعبير.
الحل:
في هذا المثال لدينا دالة أكثر تعقيدا من المثال السابق ولكن سنحسب بنفس الطريقة.
سنحسب \(y(2)\) بتعويض 2 عن t في الدالة:
\(=1+2\cdot 5+{2}^{2}\cdot 0,7-=y(2) \)
\(=1+2\cdot 5+0,7\cdot 4-=\)
\(=1+10+2,8-=\)
\(8,2=\)
ما هذا الذي حسبناه الآن؟
\(y(2)\) تعني أننا قمنا بحساب ارتفاع القذيفة عن الأرض بعد 2 ثانية من إطلاقها.
ووصلنا الى أن
\( 8,2=y(2)\)
ونفسره بأن القذيفة بعد ثانيتين كانت على ارتفاع 8,2 متر فوق سطح الأرض.
وبالمثل يمكننا حساب ارتفاع قذيفة المدفع عن سطح الأرض في أوقات أخرى. كل ما علينا فعله هو إدخال وقت معين بالثواني في الدالة ونحصل على ارتفاع القذيفة عن سطح الأرض في ذلك الوقت.
فيديوهات الدرس (باللغة السويدية)
مفهوم الدوال.
هنا نواصل في مفهوم الدوال باستخدام مفهوم آليات الدوال.
