الأعداد السالبة

في الصف الثامن تعلمنا ما هي الأعداد السالبة و تعلمنا قواعد الحساب الصالحة لجمع أو طرح الأعداد السالبة.

في هذا القسم سنكرر كيفية عمل الأعداد السالبة، وكيف يمكننا جمع وطرح هذه الأعداد، ثم نتعلم في القسم القادم كيف يمكننا ضرب وقسمة الأعداد السالبة.

الأعداد السالبة وخط الأعداد

الأعداد السالبة هي الأعداد التي تقل قيمتها عن الصفر.

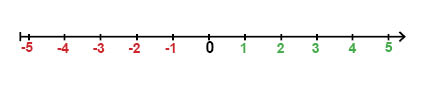
عادة ما تُسمى نقطة الصفر على خط الأعداد بنقطة الأصل. الأعداد على يمين نقطة الأصل على خط الأعداد هي الأعداد الموجبة, بينما الأعداد على يسار نقطة الأصل فهي الأعداد السالبة.

جمع وطرح الأعداد السالبة

عند جمع أو طرح الأعداد السالبة هناك قواعد حسابية معينة يجب علينا أن نتذكرها.

هل عملية جمع عدد سالب هي نفس عملية طرحه كعدد موجب.

لنرى مثال على ذلك:

\(1 = 3 - 4 = (3-) + 4\)

هل عملية طرح عدد سالب هي نفس عملية جمعه كعدد موجب.

مثال على ذلك:

\(7 = 3 + 4 = (3-) - 4\)

كما نلاحظ من المهم متابعة ترتيب العلامات المستخدمة.

هناك قاعدة يجب تذكرها وهي أن العلامات المتشابهة تعطي زائد (موجب)، بينما العلامات المختلفة تعطي ناقص (سالب):

\(1=3\,{\color{Red} -}\,4=(3{\color{Red} -})\,{\color{Blue} +}\,4\)

\(7=3\,{\color{Blue} +}\,4=(3{\color{Red} -})\,{\color{Red} -}\,4\)

أي أن علامتي ناقص يعطيان زائد:

إذا كان a و b عددين موجبين، يمكننا تلخيص هذه القواعد الحسابية على النحو التالي:

\(b-a= (b-) + a\)

\(b + a= (b-) - a\)

---

احسب

1) \((3-) + (2-) - 1\)

2) \((3-) - 2 + (1-)\)

الحل:

1) نستخدم القواعد الحسابية خطوة بخطوة:

\(= (3-) + (2-) - 1\)

\(= (3-) + 2 + 1 =\)

\(= 3 - 2 + 1 =\)

\(= 3 - 3 =\)

\(0=\)

2) نستخدم القواعد الحسابية خطوة بخطوة:

\(=(3-) - 2 + (1-) \)

\(= 3 + 2 + 1- =\)

\(= 3+1 =\)

\(4=\)

---

فيديوهات الدرس (بالسويدية)

الأعداد السالبة مع الجمع والطرح بإستخدام خط الأعداد (الخط العددي.

الأعداد السالبة مع الجمع والطرح.

في هذا الفيديو نواصل في دراسة الأعداد السالبة مع الجمع والطرح.