الأسطوانات

في الأقسام السابقة درسنا المكعبات و أشباه المكعبات وكذلك المناشير.

في هذا القسم سنتعلم الأشكال الهندسية التي تُسمى بالأسطوانات. هناك العديد من الأشياء التي تأخذ الشكل الأسطواني في الحياة اليومية، مثل علب الطعام المحفوظ وأكواب الشراب التي غالبا ما تأخذ شكل الأسطوانة.

الاسطوانة

نوع الأسطوانات الأكثر شيوعا الذي نواجهه هو ما يسمى بالأسطوانات الدائرية المُستقيمة. هذه الأسطوانات لها قاعدتان سطحيتان يأخذان شكل الدائرة. وهذان القاعدتان يرتبطان بغلاف سطحي.

فيما يلي كيف يبدو شكل الأسطوانة الدائرية المُستقيمة.

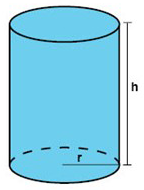
حجم الأسطوانة

لحساب حجم الأسطوانة نستخدم نفس الصيغة التي استخدمناها لحساب حجم المنشور.

بالتالي حجم الأسطوانة يساوي مساحة القاعدة B مضروبة في الارتفاع h. الارتفاع h يساوي المسافة بين القاعدتان السطحيتان. سطح القاعدة يأخذ شكل دائرة نصف قطرها r, لذا نستخدم صيغة مساحة الدائرة لحساب مساحة القاعدة.

إذن يمكننا حساب حجم الأسطوانة الدائرية المُستقيمة على النحو التالي:

الحجم = القاعدة \(\cdot\) الإرتفاع

V_{الأسطوانة الدائرية المُستقيمة} \(h\cdot \pi{r}^{2}=h\cdot B=\)

---

ما هو حجم علبة التونة؟

تُعتبر علبة التونة العادية أسطوانة. فإذا كان سطح قاعدتها يأخذ شكل دائرة نصف قطرها 4,25 سم وارتفاعها 4 سم, فما هو حجم هذه العلبة؟

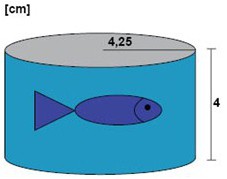
الحل:

لحساب حجم الأسطوانة نبدأ بحساب مساحة سطح القاعدة التي تأخذ شكل الدائرة.

نصف قطر الدائرة 4,25 سم، بالتالي نحصل على مساحة القاعدة كما يلي:

\({(4,25)}^{2}\cdot \pi={r}^{2}\pi=B\) \(56,7\,\approx\) سم\(^2\)

نحسب حجم الأسطوانة باستخدام مساحة القاعدة (B) والارتفاع (\(4 = h\) سم)

\(200\approx 4\cdot {(4,25)}^{2}\cdot \pi=h\cdot B=V\) سم\(^3\) = 200 مل

إذن حجم علبة التونة حوالي 200 سم\(^3\) وهو ما يعادل 200 مل.

فيديو الدرس (باللغة السويدية)

حساب حجم الأسطوانة.