التشابه

في الصف الثامن استخدمنا مقياس الرسم لتحديد تكبير أو تصغير الرسومات و الصور.

في هذا القسم سنتعلم التشابه وهو طريقة لتحديد ما إذا كان شكلين من الأشكال الهندسية لهما نفس الشكل ام لا، ولكن ليس من الضروري أن يكون لهما نفس الحجم.

التشابه

كما تعلمنا في القسم الخاص بمقياس الرسم، يمكننا على أي رسم تحديد أن طول مسافة ما هو ضعف الطول الأصلي بكتابة مقياس الرسم 1:2. فإذا كان لدينا شكل ثنائي الأبعاد ونريد رسمه بمقياس الرسم 1:2 فهذا يعني أن كل المسافات على الرسم ستكون ضعف مسافات الشكل الأصلي. بالتالي سيكون الشكل الكلي على الرسم أربعة أضعاف الشكل الأصلي.

على سبيل المثال يمكننا رسم مثلثين بحيث يكون المثلث الأصلي هو المثلث ABC وتكون صورته هي المثلث DEF بمقياس رسم 1:2 كما في الأشكال الآتية:

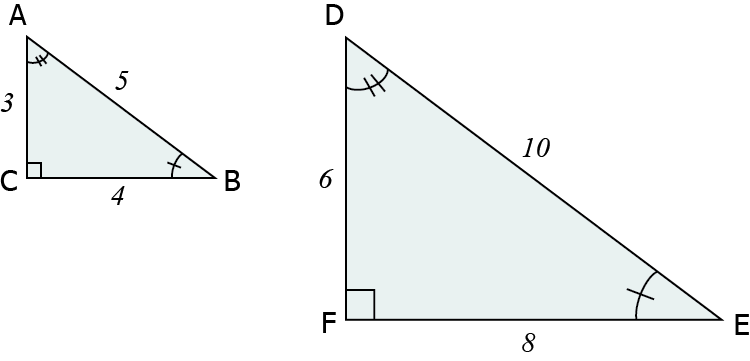
يمكن أن نلاحظ أن كل ضلع من أضلاع المثلث ABC له ضلع مشابه في المثلث DEF ويساوي ضعفه. أيضا يمكن أن نلاحظ أن لكل زاوية من زوايا المثلث ABC زاوية مشابهة في المثلث DEF وبنفس حجمها تماما. عليه فإن المثلث DEF عبارة عن أربعة أضعاف المثلث ABC.

لذلك المثلثين لهما نفس الشكل ولكنهما مختلفين في الحجم. عندما يكون لدينا مثلثين (أو أي نوع آخر من المضلعات) لهما نفس الشكل، ولكن ليس بالضرورة نفس الحجم، في هذه الحالة نقول أن الشكلان متشابهان.

تشابه الشكلين المضلعين يعني أن النسبة بين أي ضلعين متشابهين تساوي النسبة بين الأضلاع المتشابهة الأخرى. النسبة بين الأضلاع المتشابهة هي حاصل القسمة بين أطوالها. لذلك من المثلثين المتشابهين ABC و DEF في الشكل أعلاه نجد أن:

\(2=\frac{10}{5}=\frac{DE}{AB} \)

\( 2=\frac{8}{4}=\frac{EF}{BC}\)

\(2=\frac{6}{3}=\frac{DF}{AC} \)

\(2=\frac{DF}{AC}=\frac{EF}{BC}=\frac{DE}{AB}\)

بالتالي النسب بين الأضلاع المتشابهة في المثلثين أعلاه هي 2. وهذا لأن المثلثين متشابهين والمثلث DFE هو عبارة عن صورة مكبرة للمثلث الأصلي ABC, أي  أربعة أضعاف المثلث ABC.

أما إذا كانت النسب بين الأضلاع المتشابهة مختلفة فهذا يعني أن المثلثين غير متشابهين.

الحساب مع الأشكال المتشابهة

عندما يكون لدينا أشكال هندسية متشابهة، فهذا يعني أن النسب بين الأضلاع المتشابهة متساوية.

وهذا يعني أنه إذا إذا كان لدينا شكلين متشابهين ونريد معرفة طول ضلع معين, فمن ثم يمكننا استنتاج وكتابة معادلة رياضية, بحَلّ هذه المعادلة يمكننا ايجاد طول هذا الضلع. دعونا ننظر إلى مثال نستخدم فيه هذه الطريقة.

---

حدد طول الضلع المجهول

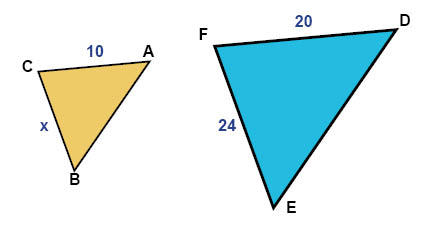
المثلثان ABC و DEF أدناه متشابهين. حدد طول الضلع BC المُسمى بالحرف x.

الحل:

بما أن المثلثين ABC و DEF متشابهين، إذن النسب بين الأضلاع المتشابهة متساوية. وهذا يعني صلاحية العلاقة التالية:

\(\frac{BC}{EF}=\frac{AC}{DF}\)

\(\frac{x}{24}=\frac{10}{20}\)

الآن تمكنا من الحصول على معادلة رياضية باستخدام النسبة بين الأضلاع المتشابهة في المثلثين. ويمكننا حل هذه المعادلة لتحديد طول الضلع BC المشار إليه بالحرف x.

حَلّ المعادلة:

\(\frac{x}{24}=\frac{10}{20} \)

\({\color{Blue}{24}\,\cdot\,}\frac{x}{24}={\color{Blue}{24}\,\cdot\,}\frac{10}{20} \)

\(x=\frac{24}{2} \)

\(12=x \therefore\)

الآن توصلنا إلى أن طول الضلع BC يساوي 12 وحدة طولية. وهذا بفضل أن المثلثين متشابهين.

---

هل المثلثين متشابهين؟

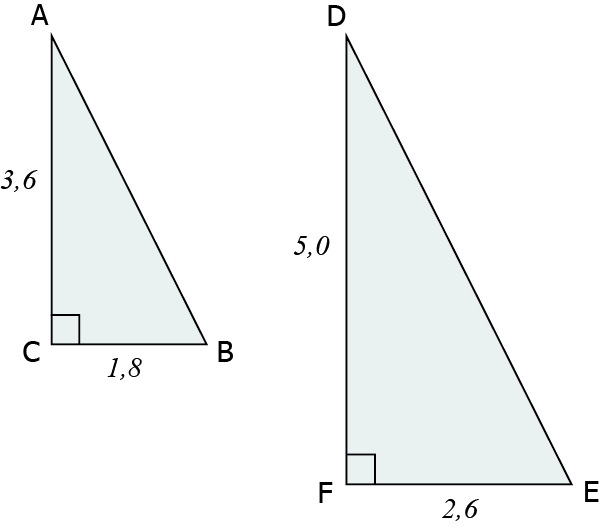
لدينا مثلثين ABC و DEF وفقا للصورة أدناه. هل المثلثان متشابهان.

الحل:

لكي يكون المثلثين ABC وDEF متشابهين، يجب أن تكون النسب بين الأضلاع المتشابهة متساوية. وهذا يمكننا التحقق منه باستخدام أطوال الأضلاع المعروفة.

إذا كان المثلثان ABC وDEF متشابهين فيجب أن تكون العلاقة التالية صالحة:

\( \frac{EF}{BC}=\frac{DF}{AC}\)

بما أننا نعلم أطوال جميع هذه الأضلاع يمكننا حساب هذه النِسب:

\(1,39\approx \frac{5,0}{3,6}=\frac{DF}{AC} \)

\(1,44\approx \frac{2,6}{1,8}=\frac{EF}{BC}\)

نلاحظ أن النسب بين الأضلاع المتشابهة مختلفة أي غير متساوية، لهذا يمكننا أن نستنتج أن المثلثين ABC و DEF غير متشابهين.

أما إذا نظرنا فقط إلى هذه الأشكال يمكننا الاعتقاد بأن المثلثين متشابهين، ولكن بعد دراسة النسب بين الأضلاع المتشابهة ومقارنتها وصلنا الى أن المثلثين غير متشابهين.

فيديوهات الدرس (باللغة السويدية)

الأشكال الرباعية المتسابهة وطريقة الضرب العكسي.

المثلثات المتشابهة وطريقة الضرب العكسي.