المُثَلَّثات
في الصف السابع تعلمنا الأنواع المختلفة للمثلثات وكيفية حساب محيط ومساحة المثلث. كما درسنا أيضا الزوايا سابقا في هذا الباب, بما في ذلك تعلمنا ما هو مجموع الزوايا.
في هذا القسم سنكرر مجموع زوايا المثلث، بعض الأنواع المختلفة للمثلث ومحيط ومساحة المثلث.
خواص المثلث
المثلث هو شكل هندسي له ثلاثة أركان متصلة مع بعضها البعض بثلاثة أضلاع. يوجد في كل ركن من أركان المثلث زاوية.
مجموع زوايا المثلث دائما يساوي °180. نحصل على مجموع الزوايا هذا بجمع الثلاث زوايا.
إذا كان لدينا مثلث على سبيل المثال، زواياه °25, °65 و °90, فسيكون مجموع الزوايا:
\({180}^{\circ}={90}^{\circ}+{65}^{\circ}+{25}^{\circ}\)
مجموع زوايا المثلث دائما °180 هي خاصية يمكن استخدامها. إذا علمنا على سبيل المثال مقدار زاويتين من زوايا المثلث يمكننا بسهولة حساب الزاوية الثالثة.
زوايا المثلث
في الشكل أدناه مثلث فيه زاويتين مقدارهما °60 و °70 كما موضح.
هل يمكن أن تكون الزاوية الثالثة \(°40 = v\)؟
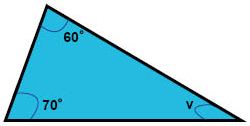
الحل:
نعلم أن مجموع زوايا المثلث دائما يكون °180. لذلك يمكننا كتابة معادلة لمجموع زوايا المثلث كما يلي:
\({180}^{\circ}=v+{70}^{\circ}+{60}^{\circ}\)
يمكن حّل هذه المعادلة كما يلي:
\({180}^{\circ}=v+{70}^{\circ}+{60}^{\circ}\)
\({180}^{\circ}=v+{130}^{\circ}\)
\({130}^{\circ}\,{\color{Red} -\,{180}^{\circ}}={130}^{\circ}{\color{Red} -\,}v\,+{130}^{\circ}\)
\({50}^{\circ}=v\)
بالتالي توصلنا إلى أن الزاوية v يجب أن تكون °50, ولا يمكن أن تكون °40.
الأنواع المختلفة للمثلث
الآن نعلم أن مجموع زوايا المثلث يجب أن يكون دائما °180. هناك ثلاثة أنواع خاصة من المثلثات الأكثر شيوعا ينبغي علينا معرفتها، لأن لها علاقات مفيدة بين زواياها وأضلاعها.
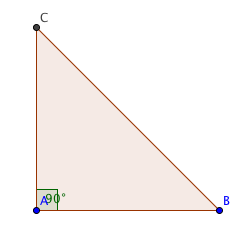
المثلثات القائمة الزاوية
المثلث القائم الزاوية هو مثلث به زاوية قائمة مقدارها °90. مثلث به زاوية قائمة يعني أن الزاويتين الآخرتين مجموعهما °90, لأن مجموع زوايا المثلث دائما °180.
المثلثات المتساوية الساقين
المثلث المتساوي الساقين هو مثلث يحتوي على ضلعين متساويين في الطول.
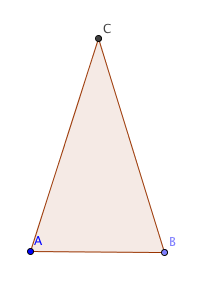
لدينا الضلعين AC و BC في المثلث أعلاه متساويين، بالتالي فإن المثلث متساوي الساقين.
من الخصائص المفيدة للمثلثات المتساوية الساقين هو أن زاويتين من زواياها متساويتين. الشكل أعلاه مثلث متساوي الساقين، فيه الزاويتين A وB متساويين ويُسميان زاويتي القاعدة.
المثلثات المتساوية الأضلاع
المثلث متساوي الأضلاع هو مثلث جميع أضلاعه متساوية في الطول.
من الخصائص الأخرى المفيدة هي أن المثلثات المتساوية الأضلاع تكون زواياها الثلاث متساوية. وبما أن مجموع زوايا المثلث يساوي °180, فكل زاوية تساوي °60:
\({180}^{\circ}=v\,3\)
\({60}^{\circ}=\frac{{180}^{\circ}}{3}=v\)
محيط ومساحة المثلثات
محيط المثلث "O" يساوي مجموع أطوال أضلاعه. بصورة عامة يمكن كتابة محيط مثلث أضلاع b ,a و c على النحو التالي:
\(c+b+a=O\)
للحصول على صيغة لمساحة المثلث قد يكون من المفيد التفكير في مثلث يُمثل نصف متوازي أضلاع.
في الشكل أدناه رسمنا متوازي أضلاع مساحته ضعف مساحة المثلث الموضح داخله.

كما نعلم من قسم الأشكال الرباعية الأضلاع، يمكن حساب مساحة متوازي الأضلاع بضرب القاعدة في الارتفاع. وبما أن مساحة المثلث هي نصف مساحة متوازي أضلاع له نفس القاعدة والارتفاع، يمكن أن نكتب مساحة المثلث على النحو التالي:
\(\frac{h\cdot b}{2}={A}\)
أحسب محيط ومساحة المثلث التالي
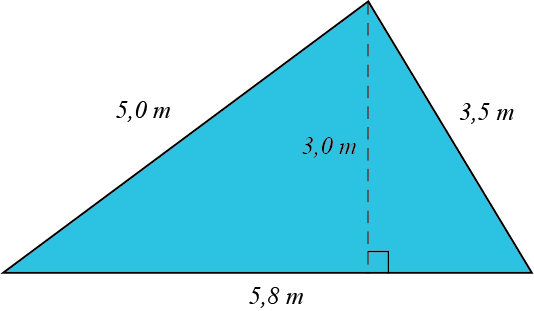
الحل:
المحيط يساوي مجموع أطوال أضلاعه، ويمكن قرأتها من الشكل:
\(14,3=5,8+5,0+3,5=O\) م
إذن محيط المثلث هو 14,3 متر.
لحساب مساحة المثلث نبدأ بتحديد القاعدة والارتفاع. من الشكل نلاحظ أن طول القاعدة يساوي 5,8 متر والارتفاع يساوي 3,0 متر. لذلك يمكننا حساب مساحة المثلث كما يلي:
\(8,7=\frac{17,4}{2}=\frac{3,0\cdot 5,8}{2}=\frac{h\cdot b}{2}=A\) م2
بالتالي مساحة المثلث تساوي 8,7 م2.
