الزوايا
في الصف السابع بدأنا نتعلم الزوايا. حيث درسنا ما هي الزاوية وكيف يمكن قياس أو رسم الزاوية باستخدام المنقلة مثلا.
في هذا القسم نستعرض بعض أنواع الزوايا التي يمكن أن نقابلها. كما سنتعلم بعض العلاقات المفيدة بين الزوايا.
أنواع الزوايا
تبدأ الزاوية من نقطة تسمى رأس الزاوية حيث يلتقي فيها ضِلعي الزاوية.
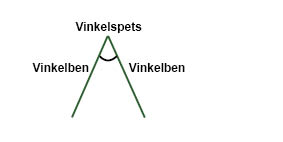
تقاس الزاوية بالدرجات ونشير إليها برمز الدرجات (°). على سبيل المثال نكتب مقياس الزاوية واحد درجة كـ °1.
هناك أسماء متنوعة للزوايا بناء على مقياس الزاوية.
تسمى الزوايا التي قياسها °90 زاوية قائمة. الزاوية القائمة تعادل ربع دورة. ويوضح الشكل أدناه الزاوية القائمة:
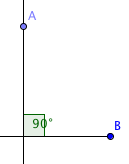
وتسمى الزوايا التي قياسها أقل من °90 زوايا حادة. ويوضح الشكل أدناه الزاوية الحادة:
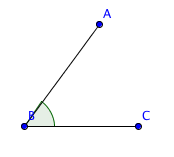
وتسمى الزوايا التي قياسها أكبر من 90 ° وأقل من °180 زوايا منفرجة. ويوضح الشكل أدناه الزاوية المنفرجة:
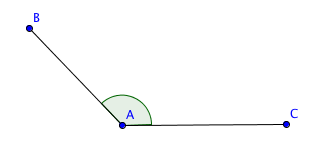
مجموع الزوايا
عندما يكون لدينا زاويتين على سبيل المثال °25 و °65, يمكننا حساب مجموعهما عن طريق إضافتهما بكل بساطة كما يلي:
مجموع الزاويتين \({90}^{\circ}={65}^{\circ}+{25}^{\circ}=\)
في هذا المثال مجموع الزاويتين معا هو °90, أي أنهما يشكلان زاوية قائمة.
القدرة على حساب مجموع الزوايا أمر هام عند دراسة خصائص الأشكال الهندسية المختلفة كالمربعات والمثلثات.
علاقات الزوايا المتجاورة والزوايا المتقابلة بالرأس
عندما نحسب أو نتعامل مع الزوايا هناك عدد من العلاقات بين زوايا معينة ومن المفيد معرفتها. وسندرس الآن علاقتين من هذه العلاقات، لاحقا في قسم المثلثات سنتعلم المزيد من هذه العلاقات.
إذا تقاطع خطين ستتكون أربع زوايا, ويمكننا أن نراهم في هذا الشكل:
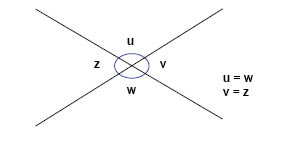
مجموع الأربع زوايا w ,v ,u و z هو °360, لأنهم يُشكلوا دورة كاملة.
تُسمى الزوايا المجاورة لبعضها البعض كما في هذا الشكل زوايا متجاورة. مجموع الزاويتين المتجاورتين دائما يساوي °180, لأنهما الاثنان معا يشكلان نصف دورة. على سبيل المثال الزاويتين u و v في الشكل هما زاويتين متجاورتين.
تُسمى الزوايا المقابلة لبعضها البعض كما في هذا الشكل زوايا متقابلة بالرأس. يوجد في الشكل زوج من الزوايا المتقابلة بالرأس، الزاويتين u و w والزاويتين v و z. الزاويتان المتقابلتان بالرأس دائما متساويتان، لهذا فإن u = w و z = v.
إيجاد مقاييس الزوايا
إذا كانت الزاوية u في الشكل أدناه تساوي °105. حدد مقياس الزوايا w ,v و z بدون قياسهم من الشكل.
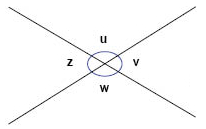
الحل:
الزاويتان u و w هما زاويتان متقابلتان بالرأس، إذن هما زاويتان متساويتان. إذن \(105^{\circ}=w\).
الزاويتان u و v هما زاويتان متجاورتان، لذا نعلم أن مجموعهما يساوي °180:
\({180}^{\circ}=v+{105}^{\circ}=v+u\)
إذن \(75^{\circ}=v\).
الزاويتان v و z أيضا متقابلتان بالرأس، بالتالي هما زاويتان متساويتان. إذن \(75^{\circ}=z\).
بالتالي توصلنا إلى مقاييس الزوايا وهي: \(75^{\circ}=v\), \(105^{\circ}=w\) و \(75^{\circ}=z\)
