حَلّ المعادلات
في الصف السابع بدأنا نتعرف على المعادلات وتعلمنا حَلّ المعادلات الذي يعني التعرف على قِيّم المتغيرات التي تجعل طرفي المعادلة لهما نفس القيم.
في هذا القسم سنتعلم الطرق المختلفة التي يمكننا استخدامها لحل المعادلات الأكثر تعقيدا.
حَلّ المعادلة
حَلّ المعادلة يعني ايجاد قِيّم المتغيرات بحيث يكون الطرف الأيسر للمعادلة مساويا للطرف الأيمن للمعادلة.
فيما يلي مثال على المعادلة
\(12=5+x\)
في هذه المعادلة الطرف الأيمن هو \(5+x\) و الطرف الأيسر هو 12. حَلّ هذه المعادلة يعني ايجاد قيمة المتغير x التي تجعل \((5+x)\) يساوي 12
حل المعادلات بطريقة الموازنة
توجد طرق مختلفة للوصول إلى حَل المعادلات. في الصف السابع قمنا بحَل معادلات من النوع:
\(12=5+x\)
وذلك بالسؤال عن ما هو العدد الذي يجب إضافته إلى 5 ليصبح الناتج 12. هذا العدد يجب أن يكون 7, بالتالي حَل هذه المعادلة هو \(7=x\).
هذه الطريقة لحَل المعادلات ستكون مُناسِبة طالما أن المعادلات ليست معقدة جدا، ولكن في هذا القسم سنتعلم استخدام طريقة أفضل.
في الحقيقة يمكننا جمع أو طرح أي عدد من طرفي المعادلة، كما يمكننا ضرب أو قسمة طرفي المعادلة مع أي عدد (باستثناء القسمة على صفر، وهو غير مسموح به على الاطلاق).
تسمى هذه الطريقة في بعض الأحيان "الموازنة", لأن هذا يعني إذا فعلنا شيء ما في أحد الطرفين فيجب أن نفعل نفس الشيء في الطرف الآخر. طالما حافظنا على هذا التوازن سيكون كلا الطرفين متساويين.
وقد يكون من المفيد التفكير في التوازن كما في الميزان القديم، حيث يجب أن تحتوي كل من كفتي الميزان على نفس الوزن لكي يكون الميزان متوازنا. إذا كان لدينا ميزان به 4 تفاحات في كل كفة فسيكون الميزان متوازنا.
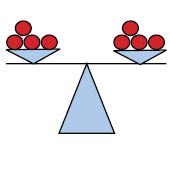
إذا أضفنا تفاحة إلى كفة اليسار يجب أن نضيف تفاحة إلى كفة اليمين لكي يظل الميزان متوازنا.
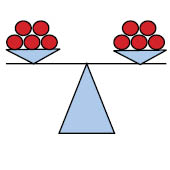
باستخدام هذا التوازن يمكننا تنفيذ العمليات الحسابية الأربع لإعادة كتابة طرفي المعادلة لكي يكون المتغير وحيد في أحد الطرفين بينما يحتوي الطرف الآخر على قيمة المتغير.
أمثلة على حَل المعادلة بالموازنة
سنعرض الآن كيف يمكننا حَل بعض المعادلات المختلفة باستخدام التوازن. أولا سنقوم بحل أربع معادلات تحتوي كل منها على إحدى العمليات الحسابية الأربعة، بعدها سنحل معادلة أكثر تعقيدا باستخدام عمليتين حسابيتين خطوة خطوة.
حِل المعادلة
\(12=5+x\)
نريد أن يكون المتغير x بمفرده في الطرف الأيمن. وهذا يمكن أن يتم بطرح 5 من طرفي المعادلة. عندها سنحصل على ما يلي:
\(12=5+x\)
\({\color{Red} {5\,-}}\,12={\color{Red} {5\,-}}\,5+x\)
\(7=x\)
حِل المعادلة
\(6=3-y\)
لحَل هذه المعادلة يجب أن يكون المتغير y بمفرده في أحد الطرفين. يمكننا الحصول على هذا بإضافة 3 إلى طرفي المعادلة:
\(6=3-y\)
\({\color{Blue}{ 3\,+}}\,6={\color{Blue} {3\,+}}\,3-y\)
\(9=y\)
حِل المعادلة
\(3=\frac{x}{6}\)
نريد أن يكون المتغير x بمفرده في أحد الطرفين. يمكن تحقيق ذلك بضرب كل من الطرفين فــي 6:
\(3=\frac{x}{6}\)
\(3\,{\color{Blue} {\cdot\, 6}}=\frac{x}{6}\, {\color{Blue} {\cdot\, 6}}\)
\(18=\frac{x6}{6}\)
\(18=x\)
حِل المعادلة
\(35=z7\)
نريد أن يكون المتغير z بمفرده في أحد الطرفين. يمكن تحقيق ذلك بقسمة كلا الطرفين علــى 7:
\(35=z7\)
\(\frac{35}{{\color{Red} 7}}=\frac{z7}{{\color{Red} {7}}}\)
\(5=z\)
حِل المعادلة
\(13=5+x4\)
هذه المعادلة أكثر تعقيدا، حيث سنستخدم فيها طريقتين حسابيتين واحدة بعد الأخرى لإيجاد الحل.
نريد أن يكون المتغير x بمفرده في أحد الطرفين. أولا سنحاول التخلص من الــ 5 وابقاء الحد \(x4\) لوحده في الطرف الأيمن، وذلك عن طريق طرح 5 من كلا الطرفين:
\(13=5+x4\)
\({\color{Red} {5\,-}}\,13={\color{Red}{ 5\,-}}\,5+x4\)
\(8=x4\)
الآن لدينا الحد المتغير \(x4\) في الطرف الأيمن. ولكن ما نريده هو أن تكون x لوحدها فقط بدون الــ 4, بالتالي يمكننا قسمة الطرفين علـى 4:
\(8=x4\)
\(\frac{8}{{\color{Blue} 4}}=\frac{x4}{{\color{Blue} 4}}\)
\(2=x\)
الآن وجدنا حل المعادلة: \(2=x\)
بهذه الطريقة يمكننا حَل معادلات أكثر تعقيدا خطوة خطوة، وهذا ما سنقوم به في القسم القادم.
