رُباعي الأضلاع
في الصف السابع بدأنا نتعلم الأشكال الرباعية وكيفية حساب محيط ومساحة أشكال رباعية مختلفة.
في هذا القسم سنكرر بعض العلاقات التي تنطبق على الأنواع المختلفة للأشكال الرباعية. كما سنبحث ما نعرفه عن مجموع الزوايا الذي ينطبق على الأشكال الرباعية الأضلاع.
الأنواع المختلفة للأشكال الرباعية الأضلاع
الشكل الرباعي الأضلاع هو شكل هندسي له أربع أركان مرتبطة مع بعضها البعض بأربعة أضلاع. تُسمى هذه الأركان بحروف مثل C ,B ,A و D. مجموع زوايا الشكل الرباعي دائما يساوي °360.
سنكرر أربعة أشكال رباعية مألوفة ونستعرض كيف نحسب محيط ومساحة هذه الأشكال: المستطيل، المربع, متوازي الأضلاع والمعين.
المستطيل
المستطيل هو شكل رباعي يحتوي على زوايا قائمة فقط.
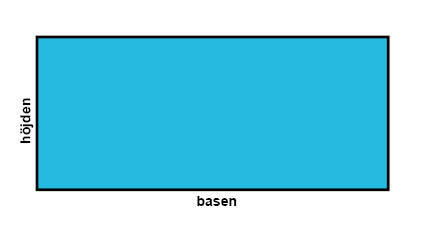
من خصائص المستطيل أنه يحتوي على زوايا قائمة فقط و الأضلاع المتقابلة في المستطيل متساوية في الطول. عندما نحسب محيط أو مساحة المستطيل عادة ما نسمي أضلاعه بالقاعدة (b) والارتفاع (h).
يمكن حساب مساحة المستطيل "O" باستخدام الصيغة التالية:
\(h2+b2=O\)
كما يمكن حساب المساحة "A" بالصيغة التالية:
\(h\cdot b=A\)
لننظر إلى المثال التالي
مستطيل قاعدته 20 سم وارتفاعه 10 سم.
أوجد مستطيل أخر له ضعف:
a) محيط هذا المستطيل.
b) مساحة هذا المستطيل.
الحل:
a)
علينا إيجاد مستطيل محيطه ضعف محيط المستطيل الذي قاعدته 20 سم وارتفاعه 10 سم.
ولأن محيط المستطيل يساوي مجموع أطوال أضلاعه، سنحتاج فقط لمضاعفة أطوال الأضلاع لكي يكون محيط المستطيل الضعف.
يمكننا حساب محيط المستطيل الصغير على النحو التالي:
Oالأصغر \(=h2+b2=\)
\(=10\cdot 2+20\cdot 2=\)
\(60=20+40\) سم
إذا قمنا بمضاعفة قاعدة وارتفاع المستطيل الصغير، عندها سنحصل على المحيط التالي:
O \(=20\cdot 2+40\cdot 2=\)
\(120=80+40=\) سم
بالتالي المستطيل الذي تكون قاعدته 40 سم وارتفاعه 20 سم لديه ضعف محيط المستطيل الذي قاعدته 20 سم وارتفاعه 10 سم.
b)
علينا إيجاد مستطيل مساحته ضعف مساحة المستطيل الذي قاعدته 20 سم وارتفاعه 10 سم.
نحسب مساحة المستطيل باستخدام الصيغة التالية
\(h\cdot b=A\)
مساحة المستطيل الصغير تساوي
Aالأصغر \(200=10\cdot 20=h\cdot b=\) سم2
مساحة المستطيل الكبير ستكون ضعف مساحة المستطيل الصغير، أي
\(\cdot 2\)Aالأصغر \(400=10ْ\cdot 20\cdot 2=h\cdot b\cdot 2=\) سم2
كيف يمكن مضاعفة مساحة المستطيل؟ يمكننا على سبيل المثال مضاعفة طول أحد الأضلاع. وهذا يعني أنه يمكن أن نجعل طول القاعدة 40 سم بدلا من 20 سم لتكون المساحة الضعف أي 400 سم2.
بالتالي المستطيل الذي تكون قاعدته 40 سم وارتفاعه 10 سم ستكون مساحته ضعف مساحة المستطيل الذي تكون قاعدته 20 سم وارتفاعه 10 سم.
المربع
المربع شبيه جدا بالمستطيل، في الواقع المربع هو مستطيل جميع أضلاعه متساوية في الطول.

جميع الأضلاع متساوية في المربع ما يعني أنه من السهل حساب محيط ومساحة المربع. للتبسيط نرمز غالبا إلى طول الضلع بالرمز "s".
نحسب المحيط "O" باستخدام الصيغة التالية
\(s4=O\)
ونحسب المساحة "A" كما يلي:
\({s}^{2}=s\cdot s=A\)
(كما رأينا في قسم الأُسُس \(s^{2}\) هي طريقة أخرى لكتابة s مضروبة في نفسها.)
متوازي الأضلاع
متوازي الأضلاع هو شكل رباعي يكون فيه الأضلاع المتقابلة متساوية في الطول.
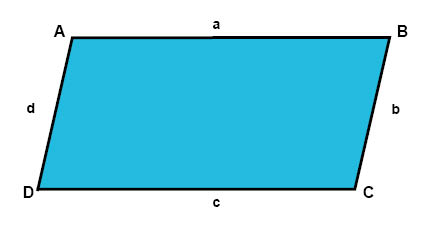
يمكن أن تكون زوايا متوازي الأضلاع زوايا قائمة ولكن ليس بالضرورة أن تكون قائمة.
إذا بدأنا من الحروف المستخدمة في تسمية الشكل أعلاه يمكننا كتابة محيط متوازي الأضلاع "O" على النحو التالي:
\(b2+a2=O\)
يمكن أن يتطلب إيجاد مساحة متوازي الأضلاع قليل من البراعة. بنفس طريقة حساب مساحة المستطيل يمكن حساب مساحة متوازي الأضلاع بضرب القاعدة في الارتفاع. ولكن قاعدة متوازي الأضلاع b هي أحد أضلاعه بينما ارتفاعه h هو المسافة العمودية بين القاعدة والضلع المقابل للقاعدة.
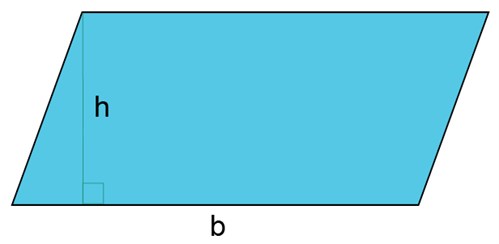
لذا نحسب المساحة A كما يلي
\(h\cdot b=A\)
المعين
المعين هو عبارة عن متوازي أضلاع جميع أضلاعه متساوية في الطول.

من السهل حساب محيط المعين "O" إذا علمنا طول ضلع المعين "s":
\(s4=O\)
عند كتابة مساحة المعين نستخدم نفس الصيغة التي استخدمناها لتحديد مساحة متوازي الأضلاع. أيضا في حالة المعين يجب أن نكون حريصين على أن يكون ارتفاعه h هو المسافة العمودية بين القاعدة والضلع المقابل للقاعدة:
\(h\cdot b=A\)
