رُباعي الأضلاع
في القسم السابق تعرفنا على الزوايا و من ضمنها الزوايا القائمة.
في هذا القسم سندرس أنواع مختلفة من الأشكال الرباعية الأضلاع و كيف يمكننا حساب محيطها و مساحتها. يمكننا استخدام ما تعلمناه عن الزوايا لتسهيل دراسة الأنواع المختلفة من الأشكال الرباعية و فهمها بصورة أفضل.
ما هو رباعي الأضلاع؟
الشكل الرباعي الأضلاع (البعض يُسميه رباعي الأركان) هو شكل هندسي له أربع أركان مُرتبطة مع بعضها البعض بأربعة أضلاع. غالبا ما نُسمي هذه الأركان بحروف، مِثل C ،B ،A و D.
أضلاع الشكل الرباعي تُسمي باستخدام رموز الأركان التي تربطها مع بعضها البعض. على سبيل المثال, الضلع الذي يربط الركنين A و B يُسمي بالضلع AB, كما في الصورة أدناه. بنفس الطريقة يمكننا على سبيل المثال أن نُسمي الضلع الذي يربط الركنين B و C معا بــ BC.
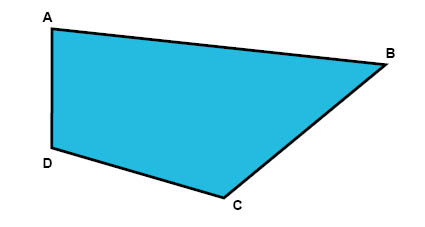
الأضلاع التي لا تلتقي في ركن من أركان الشكل الرباعي تُسمى أضلاع متقابلة. في الشكل الرباعي أعلاه الضلعان AB و CD هما ضلعان متقابلان، و الضلعان BC و AD أيضا ضلعان متقابلان.
زوايا الشكل الرباعي التي ليس لها أضلاع مشتركة (ضلع الزاوية) تُسمى زوايا متقابلة. في الشكل أعلاه زوايا الركنين A و C هما زاويتين متقابلتين، و بنفس الطريقة، زوايا الركنين B و D هما زاويتين متقابلتين.
القُطر هو الخط الذي يصل بين كل ركنين متقابلين. في الشكل أدناه تم رسم قُطريين: القُطر AC يصل بين الركنين A و C و القُطر BD يصل بين الركنين B و D.
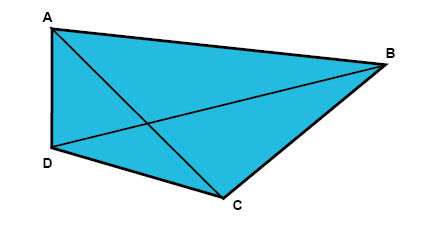
المحيط و المساحة
المحيط هو كل المسافة حول الشكل الهندسي. على سبيل المثال محيط الشكل الرباعي يساوي مجموع أطوال أضلاعه. غالبا ما نُسمى المحيط بالحرف (O) و نُميزه بــ وحدات الطول مثل المتر (م)، السنتيمتر (سم)، أو الكيلومتر (كم).
مساحة الشكل الهندسي هي المساحة السطحية للشكل. إذا كان لدينا شكل رباعي مثلا، ستكون مساحته عبارة عن المنطقة المُحددة بأضلاعه الأربعة. تُسمى المساحة غالبا بالحرف A و تُميّز بوحدات المساحة، مثل المتر المربع (م2), السنتيمتر المربع (سم2) أو الكيلومتر المربع (كم2).
مثلا عندما نقول أن مساحة ما هي 1 م2, نعني أن مساحة السطح يساوي مساحة مربع أطوال أضلاعه 1 متر. بنفس الطريق 1 سم2 هي مساحة مربع أطوال أضلاعه 1 سم.
الأنواع المختلفة لرباعيات الأضلاع
الآن سندرس بعض الأنواع المختلفة للأشكال الرباعية الأضلاع التي قد نقابلها خلال دراسة الرياضيات: المستطيل، المربع، متوازي الأضلاع و المعين. سنتعلم كيفية حساب محيط و مساحة هذه الأشكال الرباعية.
المستطيل هو شكل رباعي الأضلاع يحتوي فقط على زوايا قائمة ما يعني أن كل زاوية من هذه الزوايا الأربعة تساوي °90.
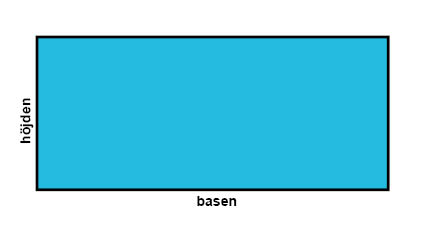
معاني الكلمات السويدية
| اللغة السويدية | اللغة العربية |
| basen | القاعدة |
| höjden | الإرتفاع |
بما أن زوايا المستطيل هي زوايا قائمة هذا يعني أن الأضلاع المتقابلة للمستطيل متساوية في الطول. عندما نحسب محيط و مساحة المستطيل، نُسمي أضلاعه بالقاعدة و الارتفاع.
محيط المستطيل يساوي مجموع أطوال أضلاعه. لذلك يمكننا حساب محيط المستطيل على النحو التالي:
المحيط = القاعدة + القاعدة + الإرتفاع + الإرتفاع =
= \(\cdot 2\) القاعدة + \(\cdot 2\) الإرتفاع
غالبا ما نسمي القاعدة بالحرف b و الارتفاع بالحرف h لذلك يمكننا كتابة المحيط O على النحو التالي:
\(2h+2b=O\)
عندما نحسب مساحة المستطيل نستخدم أيضا القاعدة و الارتفاع.
المساحة = القاعدة \(\cdot\) الإرتفاع
إذا استخدمنا الرموز A للمساحة، b (للقاعدة) و h (للارتفاع)، يمكننا كتابة مساحة المستطيل على النحو التالي:
\(h\cdot b=A\)
أحسب محيط و مساحة مستطيل ارتفاعه مترين و طول قاعدته 6 أمتار.
بما أن طول القاعدة 6 أمتار و الارتفاع 2 متر سيكون لدينا:
\(6=b\) م
\(2=h\) م
صيغة محيط المستطيل هي
\(2h+2b=O\)
لذا يمكننا حساب المحيط كما يلي
\(16=4+12=2\cdot 2+6\cdot 2=O\) م
صيغة مساحة المستطيل هي
\(h\cdot b=A\)
لذا يمكننا حساب المساحة كما يلي
\(12=2\cdot 6=A\) م2
إذن محيط المستطيل 16 متر و مساحته 12 م2.
المُربع
المربع هو عبارة عن مستطيل جميع أضلاعه متساوية في الطول.
هذا يعني أنه سيكون من الأسهل حساب محيط و مساحة المُربع. لأن الأضلاع متساوية في الطول، عادة ما نطلق عليها ببساطة ضلع المربع، و نرمز إليه بالحرف s.

| اللغة السويدية | اللغة العربية |
| sidan | تعني الضِلع في هذه الحالة |
محيط المربع يساوي مجموع أطوال أضلاعه كما يلي:
المحيط = الضِلع + الضِلع + الضِلع + الضِلع = \(\cdot 4\) الضِلع
إذا استخدمنا الحرف O لمحيط المربع و s لطول ضلع المربع، سيكون المحيط على النحو التالي:
\(4s=O\)
لحسب مساحة المربع نبدأ من صيغة مساحة المستطيل. ولأن أضلاع المربع جميعها متساوية، سنحصل على الصيغة التالية لمساحة المربع:
المساحة = الضِلع \(\cdot\) الضِلع
باستخدام الحرف A للمساحة و الحرف s للضلع نحصل على
\(s\cdot s=A\)
متوازي الاضلاع
متوازي الأضلاع هو شكل رباعي الأضلاع يكون فيه كل ضلعين متقابلين متساويين في الطول.
اختلافه من المستطيلات و المربعات هو أن زوايا متوازي الأضلاع ليست بالضرورة أن تكون قائمة. و لكن قد تكون زاويا متوازي الأضلاع قائمة.
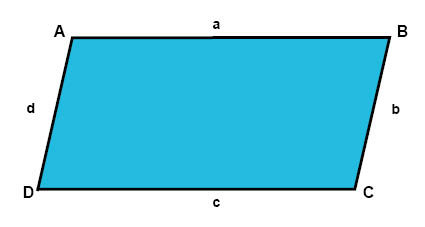
في متوازي الأضلاع تكون الأضلاع المتقابلة متساوية في الطول. انظر في الشكل أعلاه، أي أن:
\(c=a\)
\(d=b\)
بما أن الأضلاع المتقابلة متساوية في الطول، يمكننا كتابة محيط متوازي الأضلاع (O) على النحو التالي:
\(2b+2a=O\)
أنظر الى الضلعين a و b في الشكل أعلاه.
توجد صعوبة بسيطة لإيجاد مساحة متوازي الأضلاع. بنفس طريقة مساحة المستطيل سنحسب مساحة متوازي الأضلاع بضرب القاعدة في الارتفاع. قاعدة متوازي الأضلاع هي أحد أضلاعه b و لكن ارتفاعه h هو المسافة العمودية بين القاعدة و الضلع المقابل للقاعدة و يمكن رسم الإرتفاع بإستخدام المنقلة و المسطرة كما في الشكل التالي.
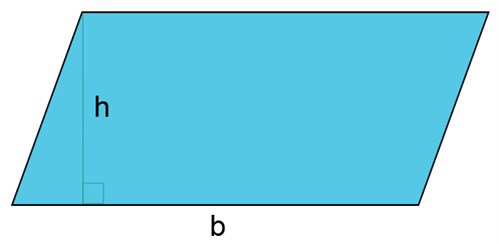
لذا سنحسب مساحة متوازي الأضلاع على النحو التالي:
\(h\cdot b=A\)
المُعيّن
المُعيّن هو عبارة عن متوازي أضلاع جميع أضلاعه متساوية في الطول.

من السهل حساب محيط المعين O إذا علمنا طول ضلع المعين s:
\(4s=O\)
لكتابة مساحة المعين نستخدم نفس الصيغة التي استخدمنها لمساحة متوازي الأضلاع:
\(h\cdot b=A\)
حيث أن القاعدة b هي أحد أضلاع المعين و الارتفاع h هو المسافة العمودية بين القاعدة والضلع المقابل للقاعدة.
