الجداول و الرسوم البيانية

في الأبواب السابقة تدربنا على العمليات الحسابية الأربعة و تعلمنا كيفية حساب النسبة المئوية.

في هذا القسم سنستخدم ما تعلمناه من العمليات الأربعة و النسبة المئوية، عندما نبدأ الآن في التعرف على مادة الإحصاء و نرى كيف يمكننا استخدام الجداول و الرسوم البيانية.

الدراسة الإحصائية

تخيل أنك تريد معرفة عدد زيارات طلاب أحد الفصول الدراسية للسينما في العام الماضي.

إذا كان هناك 20 طالبا في الفصل و سألنا كل طالب منهم عن عدد زياراته للسينما في العام الماضي، يمكننا على سبيل المثال الحصول على النتيجة التالية: 5 أشخاص ذهبوا إلى السينما 0 مرة أي لم يذهبوا، ثلاثة أشخاص ذهبوا إلى السينما مرة واحدة، أربعة أشخاص ذهبوا إلى السينما مرتين، شخصان ذهبا إلى السينما 3 مرات، 5 أشخاص ذهبوا إلى السينما 4 مرات و شخص واحد ذهب إلى السينما 5 مرات.

هذا هو ما يُسمي بالدراسة الإحصائية، بمعنى أننا قمنا بتجميع البيانات لاستخدامها لاحقا.

حتى بالنسبة لمثل هذه الدراسة الصغيرة سرعان ما يصبح من الصعب الحصول على نظرة عامة على النتائج. طريقة الحصول على فكرة أفضل عن نتائج الدراسة الاحصائية هي جمع هذه البيانات في جدول تكراري.

الجداول التكراري

الجدول التكراري يوضح كم عدد الزيارات في كل إجابة حسب الدراسة الإحصائية أعلاه. الإجابة على السؤال (كم عدد مرات زيارة السينما؟) سيكون بلا أو نعم، سنُسمي عدد الإجابات المتشابهة بــ تكرار الإجابة.

في الدراسة الاحصائية حصلنا على 6 إجابات مختلفة، بما أن اجابات الطلاب عن ذهابهم إلى السينما كانت 0, 1, 2, 3, 4, أو 5 مرات. لذا يمكننا إنشاء الجدول التكراري أدناهـ:

عدد زيارات السينما	التكرار
0
1
2
3
4
5

في العمود الأول يمكننا قرأت عدد الزيارات إلى السينما، على سبيل المثال في الصف الرابع لدينا 3 زيارات للسينما. 

في العمود الفارغ ندخل عدد مرات الحصول على كل إجابة، على سبيل المثال، لدينا طالبين أجابوا بأنهم ذهبوا إلى السينما 3 مرات، لذا سندخل الــ 2 في نفس صف الــ3 زيارات. ثم نكمل الجدول التكراري على هذا النحو:

عدد زيارات السينما	التكرار
0	5
1	3
2	4
3	2
4	5
5	1

في بعض الدراسات الإحصائية قد يكون كافيا كتابة النتائج في جدول تكراري بهذه الطريقة. في حالات أخرى قد نحتاج الى توضيح أكثر من هذا, عندئذ‏ يمكننا استخدام الرسم البياني.

الرسوم البيانية 

الرسم البياني هو طريقة لتوضيح نتائج الدراسة الإحصائية بيانيا. هناك العديد من أنواع الرسوم البيانية المختلفة و سنعرض هنا بعض أنواع الرسوم البيانية الأكثر شيوعا.

الرسم البياني العمودي

عندما يكون لدينا جدول تكراري مكتمل من السهل إنشاء رسم بياني عمودي. 

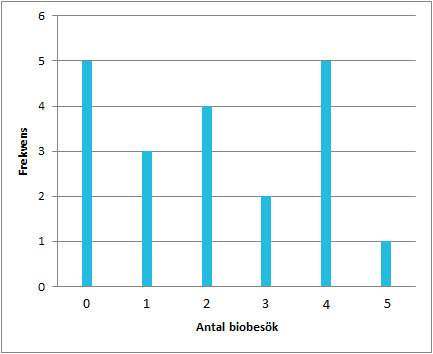
معاني الكلمات السويدية

اللغة السويدية	اللغة العربية
Antal biobesök	عدد زيارات السينما
Frekvens	التكرار

في الرسم البياني العمودي ستكون خيارات الإجابات المختلفة على المحور الأفقي (عدد زيارات السينما) و التكرار على المحور الرأسي. كل قيمة في الرسم البياني يتم تحديدها بعمود نحيف.

إذا نظرنا على سبيل المثال إلى الرسم البياني العمودي أعلاه, يمكننا من العمود الثالث قراءة أن 4 أشخاص أجابوا بأنهم ذهبوا إلى السينما مرتين في السنة الماضية.

من المناسب استخدام الرسم البياني العمودي عندما تكون هناك دراسة إحصائية فيها قيم مُعقدة، كتكرار الخيارات. (على سبيل المثال ربما يذهب الشخص إلى السينما مرة، مرتين, 3 مرات ... إلخ).

الرسم البياني الشريطي

هناك العديد من أوجه الشبه بين الرسم البياني العمودي و الرسم البياني الشريطي و لكن على المحور الأفقي للرسم البياني الشريطي عادة ما تُعرض أشياء أخري بدلا من الأعداد بالإضافة لذلك شرائطه أعرض من أعمدة الرسم البياني العمودي.

على سبيل المثال ربما نسأل 1000 شخص عما إذا فكروا في الذهاب إلى السينما هذا الشهر، بحيث يختاروا إجاباتهم من الخيارات التالية: "نعم", "لا" و "لا أعرف". حينئذ‏ سنحصل على الرسم البياني الشريطي التالي:

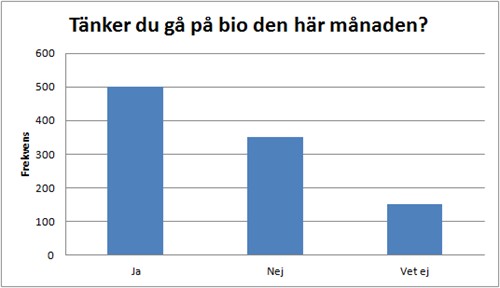
معاني الكلمات السويدية:

اللغة السويدية	اللغة العربية
?Tänker du gå på bio den här månaden	هل ستذهب الى السينما في هذا الشهر؟
Frekvens	التكرار
Ja	نعم
Nej	لا
Vet ej	لا أعرف

الرسم البياني الخطي

هناك نوع من الرسوم البيانية مختلف تماما وهو الرسم البياني الخطي الذي غالبا ما يستخدم في عرض الأشياء التي تتغير مع الزمن. عند إنشاء رسم بياني خطي نضع أولا علامة لكل نقطة ثم نرسم خطوط بين هذه النقاط التي تأتي كل منها تلو الأخرى في تسلسل زمني.

على سبيل المثال يمكنك خلال الأسبوع الدراسي أن تقرأ درجة الحرارة على الترمومتر في كل صباح قبل ذهابك إلى المدرسة. و يمكنك أن تنشئ رسم بياني خطي يوضح كيفية تغير درجة الحرارة خلال الأسبوع. كما في الرسم التالي:

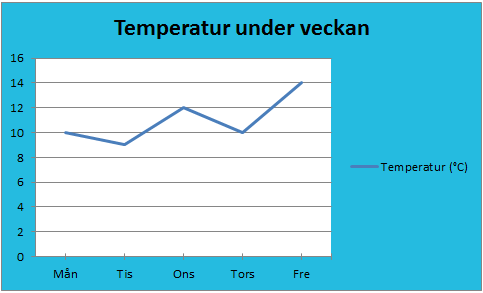
معاني الكلمات السويدية:

اللغة السويدية	اللغة العربية
Temperatur under veckan	درجة الحرارة خلال الاسبوع
Temperatur	درجة الحرارة
C\(\circ \)	درجة مئوية
Mån = Måndag	يوم الإثنين‏
Tis = Tisdag	الثلاثاء‏
Ons = Onsdag	الأربعاء‏
Tors = Torsdag	الخميس‏
Fre = Fredag	يوم الجمعة‏

في هذا المثال نلاحظ أن أيام الأسبوع المدرسي (من الاثنين إلى الجمعة حسب النظام في السويد) على المحور الأفقي للرسم البياني الخطي. كما نلاحظ على المحور الرأسي درجات الحرارة (بالدرجة المئوية °C).

الرسم البياني الدائري

إذا أردنا توضيح ما هو الجزء من الكل لشيء ما يمكننا استخدام الرسم البياني الدائري.

على سبيل المثال يمكننا حساب النِسب المئوية للإجابات التي حصلنا عليها من الدراسة الإحصائية لعدد زيارات السينما. وذلك باستخدام العلاقة بين النسبة، الجزء و الكل التي رأيناها سابقا.

إذا أردنا حساب نسبة الإجابة التي كانت 0 مرة زيارة للسينما (إجابة الذين لم يذهبوا الى السينما) وهي تعتبر جزء من الاجابات، من الجدول التكراري نلاحظ أن هناك 5 أشخاص أجابوا بهذه الاجابة أي لدينا 5 إجابات بــ 0 وهي تُمثل الجزء. العدد الكلي كان 20 شخصا أجابوا في هذه الدراسة الإحصائية أي أن عدد الإجابات الكلي كان 20 وهي تُمثل الكل، بالتالي يمكن حساب نسبة الذين أجابوا بـ 0 مرة كما يلي

النسبة = الجزء ÷ الكل = \(25\,\%=\frac{1}{4}=\frac{5}{20}\)

بنفس الطريقة يمكننا حساب نِسب الإجابات الأخرى في هذه الدراسة الاحصائية. لذا يمكننا توسيع الجدول التكراري بإضافة عمود يحتوي على الإجابات في صورة نسبة مئوية:

عدد زيارات السينما	التكرار	النسبة
0	5	25%
1	3	15%
2	4	20%
3	2	10%
4	5	25%
5	1	5%

الآن يمكننا إنشاء رسم بياني دائري لهذه الأجزاء. الرسم البياني الدائري هو ببساطة دائرة مقسمة إلى عدد من الأجزاء، أي قطاعات دائرية يعتمد حجم كل منها على مقدار الجزء الذي يُمثله. على سبيل المثال القطاع الذي يمثل النسبة %25 أكبر من القطاع الذي يُمثل النسبة %15.

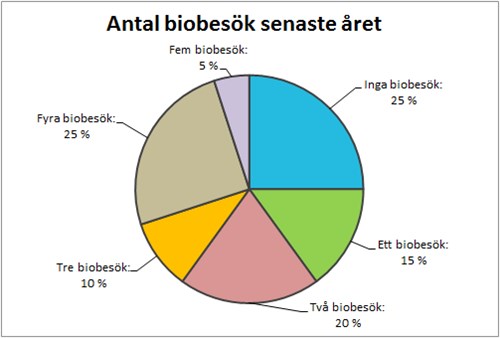
اللغة السويدية	اللغة العربية
Antal biobesök senaste året	عدد زيارات السينما في العام الماضي
Inga biobesök	لا توجد زيارة للسينما
Ett biobesök	زيارة واحدة للسينما
Två biobesök	زيارتين للسينما
Tre biobesök	ثلاث زيارات للسينما
Fyra biobesök	أربع زيارات للسينما
Fem biobesök	خمس زيارات للسينما

---

فيديو الدرس (بالسويدية)