المثلثات

في الأقسام السابقة تعلمنا أنواع مختلفة من الزوايا و الأشكال الرباعية الأضلاع.

في هذا القسم سنتعلم المثلثات و الأنواع المختلفة للمثلثات و كيف يمكننا حساب محيط و مساحة المثلثات.

ما هو المثلث؟

المثلث هو شكل هندسي له ثلاثة أركان (رؤوس) متصلة بثلاثة أضلاع. يحتوي كل ركن (رأس) من أركان المثلث على زاوية.

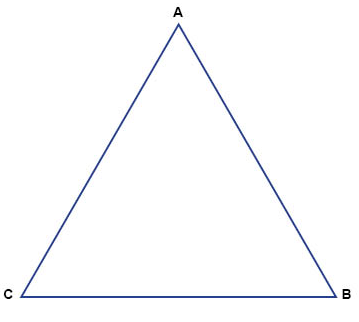
غالبا ما تُسمي أركان المثلث بحروف كبيرة، على سبيل المثال B ,A و C كما في الصورة أعلاه. عندما نقول المثلث ABC فإننا ببساطة نعني مثلث أركانه B ,A و C و نرمز للمثلث بــ ABC∆. كما نرمز إلى زاوية الركن A بالزاوية A.

في المثلث نطلق على الضلع المقابل للرأس A بالضلع المقابل للزاوية A و عادة ما نرمز له بحرف صغير. على سبيل المثال الضلع المقابل للرأس A نرمز إليه بالحرف a, فعندما يكون لدينا مثلث ABC∆, سنرمز لأضلاعه بالحروف الصغيرة ,a b و c.

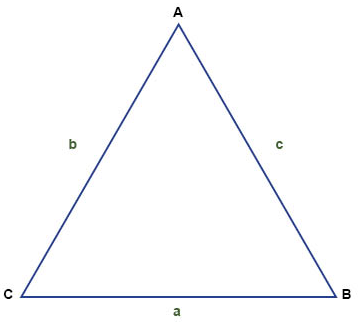
مجموع زاويا المثلث (°180)

أحد الخصائص المهمة للمثلث هو أن مجموع زواياه دائما يساوي °180. نحصل على مجموع زوايا المثلث عن طريق جمع زوايا المثلث الثلاث. وهذا المجموع يجب أن يكون دائما مساويا لـ °180.

مثلا إذا كان لدينا مثلث زواياه °80, °70 و °30, سيكون مجموع الزوايا

\({180}^{\circ}={30}^{\circ}+{70}^{\circ}+{80}^{\circ}\)

يمكننا الاستفادة من خاصية أن مجموع الزوايا يجب أن يساوي °180 في العديد من المواقف. على سبيل المثال إذا علمنا مقدار زاويتين من زوايا المثلث يمكننا حساب مقدار الزاوية الثالثة. بحيث يمكن حساب الزاوية الثالثة عن طريق طرح مجموع الزاويتين المعروفتين من °180.

حساب مقدار الزاوية المجهولة

إذا كان اثنان‏ من زاويا مثلث هما °60 و °70.

ما هو مقدار الزاوية الثالثة لهذا المثلث (الزاوية المشار إليها بالحرف v في الشكل أدناه)

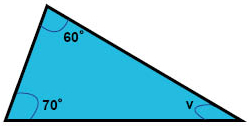
بما أننا نعرف أن مجموع زوايا المثلث هو °180 يمكننا كتابة معادلة لمجموع الزوايا على النحو التالي:

\({180}^{\circ}=v+{60}^{\circ}+{70}^{\circ}\)

رأينا سابقا كيفية حل المعادلة لهذا النوع من المعادلات. المطلوب هو ببساطة إيجاد قيمة v التي تجعل طرفي المعادلة متساويين.

لحل هذه المعادلة نبدأ أولا بتبسيط الطرف الأيمن وذلك بجمع الزاويتين المعروفتين:

\({180}^{\circ}=v+{130}^{\circ}\)

إذن لكي يتساوى طرفي هذه المعادلة يجب أن يساوي مقدار الزاوية \(v\) \({50}^{\circ}\) وذلك لأن

\({180}^{\circ}={50}^{\circ}+{130}^{\circ}\)

بالتالي مقدار الزاوية المجهولة \({50}^{\circ}=v\).

أنواع المثلث

يمكننا تقسيم المثلثات إلى أنواع مختلفة وفقا لمقادير الزوايا المختلفة للمثلث. سندرس ثلاثة أنواع خاصة من المثلثات التي تقابلنا في كثير من الأحيان، و سيكون من الجيد معرفتها.

المثلثات القائمة الزاوية

المثلث القائم الزاوية هو مثلث أحد زواياه قائمة أي مقدارها °90.

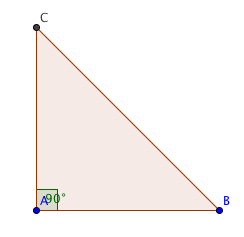
في المثلث قائم الزاوية تكون الزاوية القائمة دائما هي أكبر زواياه ويكون مجموع الزاويتين الآخرتين يساوي °90. في الشكل أعلاه زاوية الرأس A هي الزاوية القائمة و مجموع زاويتي الرأسين B و C يجب أن يساوي °90.

واحد من الخصائص الأخرى المهمة للمثلث القائم الزاوية هي أن ضلع المثلث المقابل للزاوية القائمة هو أطول أضلاع المثلث. في الشكل أعلاه زاوية الرأس A زاوية قائمة، بالتالي أطول ضلع في المثلث هو الضلع المقابل لها أي الضلع BC.

المثلثات المتساوية الساقين

المثلث المتساوي الساقين هو مثلث يحتوي على ضلعين متساويين في الطول.

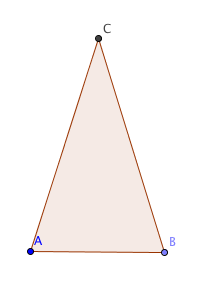
في الشكل أعلاه الضلعين AC و BC متساويين في الطول، بالتالي المثلث هو مثلث متساوي الساقين.

وجود ضلعين متساويين في المثلث يعني وجود زاويتين متساويتان في هذا المثلث. في الشكل أعلاه زوايا الرأسين A و B متساويين. تُسمى الزاويتين المتساويتين في المثلث المتساوي الساقين بزوايا القاعدة.

المثلثات المتساوية الأضلاع

المثلث متساوي الأضلاع هو مثلث جميع أضلاعه متساوية في الطول.

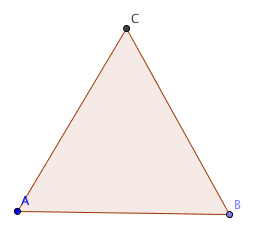
في الشكل أعلاه الأضلاع AC ,AB و BC متساوية في الطول بالتالي المثلث متساوي الأضلاع.

أضلاع المثلث الثلاثة متساوية تعني أن جميع زواياه متساوية. وبما ان مجموع هذه الثلاث زوايا المتساوية يجب أن يساوي °180 إذن يجب أن يساوي مقدار كل زاوية °60.

و العكس صحيح، إذا كان لدينا مثلث زواياه الثلاثة متساوية، فيجب أن يكون هذا المثلث متساوي الأضلاع.

محيط المثلث

في قسم رُباعي الأضلاع وصلنا إلى أن محيط الشكل الرباعي يساوي مجموع أطوال أضلاعه الأربعة. 

بنفس الطريقة يمكننا حساب محيط المثلث على أنه هو مجموع أضلاع المثلث الثلاث. إذا رمزنا إلى الأضلاع بالحروف b ,a و c, بالتالي يمكننا كتابة محيط المثلث O على النحو التالي:

\(c+b+a=O\)

مساحة المثلث

لحساب مساحة المثلث نبدأ بالرجوع الى صيغة مساحة المستطيل. مساحة المستطيل تساوي القاعدة مضروبة في الارتفاع:

\(A\)_{المستطيل} = \(h\cdot b\)

إذا تخيلنا أننا لدينا مستطيل ثم قسمناه برسم أحد أقطاره، سنحصل على مثلثين متساويين و كل منهما قائم الزاوية. أنظر الى الشكل أدناه.

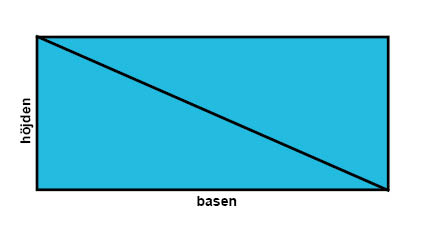
مساحة هذين المثلثين القائمين الزاوية يجب أن تساوي مساحة المستطيل، بالتالي ستكون مساحة كل مثلث من هذين المثلثين القائمين الزاوية كما يلي 

\(A\)_{مثلث قائم الزاوية} = \(\frac{h\cdot b}{2}\)

حيث أن القاعدة b و الارتفاع h هما ضلعي الزاوية القائمة.

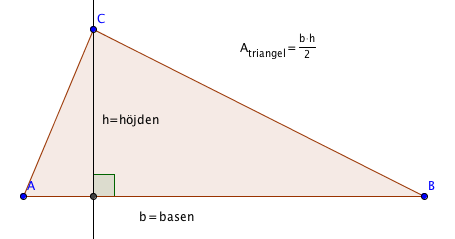
ولكن ليس كل المثلثات قائمة الزاوية. إذا كان لدينا مثلث ليس قائم الزاوية، سنستخدم نفس الصيغة لحساب المساحة ولكن يكون الارتفاع h مختلفا.

\(A\)_المثلث = \(\frac{h\cdot b}{2}\)

يجب أن يكون الارتفاع h دائما عمودي على القاعدة b. ويمكننا رسم ارتفاع المثلث كما في الشكل أدناه.

معاني الكلمات السويدية

اللغة السويدية	اللغة العربية
triangel	مثلث
basen	القاعدة
höjden	الإرتفاع

حساب محيط و مساحة المثلث

أطوال هذه الأضلاع بالسنتيمتر.

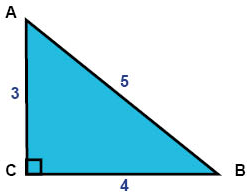
نعرف أن محيط المثلث يساوي مجموع أطوال أضلاعه، بالتالي نحصل على المحيط كما يلي:

\(O\)_المثلث = \(12=3+4+5\) سم

في الشكل نلاحظ أن زاوية الرأس C هي زاوية قائمة. إذن فهو مثلث قائم الزاوية. هذا يجعل من السهل حساب مساحة المثلث.

نفترض أن الضلع BC هو قاعدة المثلث و الضلع AC هو ارتفاع المثلث، بالتالي يمكننا حساب مساحة المثلث على النحو التالي:

\(A\)_المثلث = \(\frac{12}{2}=\frac{3\cdot 4}{2}=\frac{h\cdot b}{2}\) = 6 سم²

أي أن محيط المثلث يساوي 12 سم و مساحته تساوي 6 سم².

---

فيديو الدرس (بالسويدية)