الكسور الاعتيادية
تعلمنا في السابق الأعداد الطبيعية و الأعداد العشرية و كررنا كيفية استخدام العمليات الحسابية الأربعة عندما نجري العمليات الحسابية مع الأعداد.
في هذا القسم سنتعلم المزيد عن الكسور الاعتيادية و في الأقسام القادمة سنستخدم الكسور الاعتيادية في سياقات مختلفة.
ما هو الكسر الاعتيادي؟
تخيل أن لدينا كعكة و قسمناها إلى أربع قطع متساوية. كل قطعة من الكعكة تشكل ربع الكعكة الكاملة. يمكننا كتابة الربع كما يلي:
\(\frac{1}{4}\)
بنفس الطريقة يمكننا ان نكتب ثلاثة أرباع كما يلي:
\(\frac{3}{4}\)
بالثلاثة أرباع نعني أننا قسمنا شيئا ما إلى أربعة أجزاء متساوية بحيث ثلاثة أجزاء منها هي الثلاثة أرباع.
عندما نكتب عدد في هذه الصورة نطلق عليه كسر اعتيادي.
الأعداد المكتوبة في شكل الكسور الاعتيادية تتألف من الأجزاء التالية:
خط الكسر الاعتيادية،
البسط (العدد الذي يقع فوق خط الكسر الاعتيادي)
و المقام (العدد الذي يقع تحت خط الكسر الاعتيادي).

في مثال الكعكة أعلاه الـ 3 هي البسط و الـ 4 هي المقام.
الجزء من الكل
طريقة تفسير مفهوم الكسر الاعتيادي هي أن المقام يبين كمية الشيء كله (الكل). على سيبيل المثال قسمنا كعكة إلى أربعة قطع, فسيكون الكل هو فقط الأربع قطع معا. البسط في الكسر الاعتيادي يشير إلى كمية الجزء من الكل التي تُثير اهتمامنا، تخيل ثلاثة من أربع قطع كما في مثال الكعكة.


فكلما تم تقسيم شيء ما إلى قطع كلما حصلنا على قطع أصغر. إذا كان لدينا كعكة و قسمناها إلى قطعتين متساويتين, ستكون كل قطعة عبارة عن نصف الكعكة. و إذا قمنا بدلا من ذلك بتقسيم الكعكة إلى ثلاثة قطع متساوية ستكون كل قطعة عبارة عن ثلث الكعكة، و الثلث أقل من النصف.
\(\frac{1}{3}\)
وهو أقل من
\(\frac{1}{2}\)
كلما كبر مقام الكسر كلما كان الجزء أقل.
يمكننا استخدام الكسور الاعتيادية في سياقات مختلفة لتوضيح العلاقة بين الجزء و الكل.
اذا كان لدينا فصل دراسي يحتوي على 16 طالب, 9 منهم بنات و 7 منهم أولاد، يمكن القول أن الفصل الدراسي عبارة عن تسعة من ستة عشر طالبة و سبعة من ستة عشر طالب. يمكننا كتابة عدد البنات في شكل كسر كما يلي
\(\frac{9}{16}\)
و عدد الأولاد في شكل الكسر التالي
\(\frac{7}{16}\)
الكسور في أبسط صورة
إذا كان لدينا كعكة و قسمناها إلى أربع أجزاء متساوية يمكن أن نُعبّر عن قطعتين منها في صورة كسر اعتيادي بهذه الطريقة:
\(\frac{2}{4}\)
إذا كان لدينا قطعتي كعكة من هذه القطع الأربعة، فهما عبارة عن نصف الكعكة الكاملة. وهو نفس المقدار كما لو قسمنا الكعكة من البداية إلى قطعتين. بمعني أن الربعين هما النصف و نكتبه في صورة كسر كما يلي:
\(\frac{1}{2}\)
وهذا يعني أن
\(\frac{1}{2}=\frac{2}{4}\)
إذن الربعان يساويان النصف.
كتابة الكسر الاعتيادي بحيث يكون المقام أصغر ما يمكن تُسمي كتابة الكسر في أبسط صورة.
اكتب الكسر الاعتيادي \(\frac {3}{12}\) في أبسط صورة
يمكن أن نتخيل أن لدينا كعكة قسمناها إلى اثنى عشر قطعة متساوية. ثم نتخيل ثلاثة قطع منها. هذه الثلاث قطع هي نفس المقدار كما لو قسمنا الكعكة من البداية إلى أربعة قطع متساوية. تخيل قطعة من هذه الأرباع.
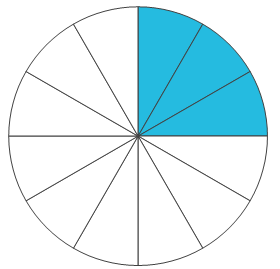
\(\frac{3}{12}\)

\(\frac{1}{4}\)
هذا يعني أن الثلاثة قطع تساوي قطعة واحدة من هذه الأرباع:
\(\frac{1}{4}=\frac{3}{12}\)
الربع هو ثلاث من اثني عشر في أبسط صورة كسرية.
الكسور في صور ممزوجة
لدينا ثلاث كعكات متشابهة و قسمنا كل منها إلى أربعة قطع متساوية. بمعني أن تم تقسيمهم الي اثنى عشر ربع:
\(\frac{12}{4}\)
فإذا أكلنا سبع من هذه القطع سيتبقى خمس قطع من الكعك، وهي عبارة عن خمسة أرباع من الكعك:
\(\frac{5}{4}\)
كتابة العدد خمسة أرباع بهذه الطريقة تسمي صورة كسرية.
يمكننا أيضا كتابة هذا العدد في صورة ممزوجة، هذا يعني أنه يمكننا تقسيم العدد إلى جزئين هما عدد صحيح و كسر اعتيادي. في مثال الكعكة يمكننا أن نقول أن الخمسة أرباع هي عبارة عن كعكة كاملة (أربعة أرباع كعكة) زائد ربع كعكة. ويمكننا كتابة هذا في صورة ممزوجة:
\(1\frac{1}{4}\)
كمثال آخر يمكننا كتابة العدد
\(\frac{11}{3}\)
في صورة ممزوجة، نحاول أولا قسمة 11 علــى 3. نلاحظ أنه سنحصل على خارج قسمة 3 و الباقي 2, لأن
\(11=2+3×3\)
وهذا يعني أنه يمكننا كتابة الكسر الاعتيادي إحدى عشر ثلث (إحدى عشر علــي ثلاثة) في صورة ممزوجة على النحو التالي:
\(3\frac{2}{3}\)
الأعداد الكسرية في صورة عشرية
رأينا أنه يمكننا كتابة الأعداد الكسرية في صورة كسور اعتيادية و صورة ممزوجة. يمكننا أيضا كتابة الأعداد الكسرية في صورة أعداد عشرية.
لكتابة العدد الكسري في صورة عدد عشري يجب أن نحسب حاصل القسمة سنحصل على ناتج في صورة عدد عشري.
إذا أردنا مثلا كتابة الكسر الاعتيادي التالي في صورة كسر عشري
\(\frac{1}{4}\)
و حسبنا ناتج هذه القسمة سنحصل على
\(0,25=\frac{1}{4}\)
في بعض الأحيان قد يكون من الأفضل كتابة الأعداد الكسرية الاعتيادي في صورة عشرية بدلا من الكسر الاعتيادي أو الصورة الممزوجة. لكن في بعض الأحيان قد يكون أيضا من الأفضل تجنب الصورة العشرية. إذا كان لدينا مثلا الكسر الاعتيادي التالي
\(\frac{1}{3}\)
و حاولنا حساب خارج القسمة سيكون الناتج حوالي 0,33. في الواقع نحتاج إلى كتابة الرقم 3 في شكل كسور عشرية لا نهائية. يمكننا إذا أردنا كتابة الثلث في صورة كسر عشري كما يلي:
\(0,33\approx\frac{1}{3}\)
في هذه المواقف من الأفضل كتابة العدد في صورة كسر اعتيادي بدلا من كتابته في صورة كسر عشري.
فيديو الدرس
اليكم بعض الأمثلة علي الكسور.
