الوسط الحسابي و الوسيط
في القسم السابق بدأنا بدراسة الإحصاء و كيف يمكننا عرض نتائج الدراسات الإحصائية باستخدام الجداول و الرسوم البيانية. استخدام الرسوم البيانية هي طريقة لتوضيح أو عرض نتائج الدراسات الإحصائية بيانيا.
في هذا القسم سندرس نوعين مما يعرفان بالمقياسان الموضعيان، تحديدا الوسط الحسابي و الوسيط.
الوسط الحسابي
عندما نتحدث عن الوسط الحسابي لمجموعة من الأعداد فإننا نعني القيمة المتوسطة (المتوسط) لهذه المجموعة من الأعداد. الوسط الحسابي هو قيمة وحيدة وهي التي تعطينا تقدير تقريبي لقِيَم المجموعة.
لنرى في المثال التالي حساب الوسط الحسابي لمجموعة من القِيَم.
في قسم الجداول و الرسوم البيانية قمنا بإنشاء رسم بياني خطي يوضح كيفية تغير درجة الحرارة خلال أسبوع مدرسي معين. يمكننا كتابة درجات الحرارة هذه في جدول كما يلي:
| اليوم | درجة الحرارة (°C) |
| الإثنين | 10 |
| الثلاثاء | 9 |
| الأربعاء | 12 |
| الخميس | 10 |
| الجمعة | 14 |
يمكن حساب الوسط الحسابي لمجموعة من القِيَم بجمع كل القِيَم ثم نقسم المجموع الذي حصلنا عليه على عدد القِيَم.
بالتالي يمكننا حساب الوسط الحسابي بصورة عامة كما يلي:
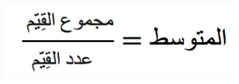
إذن متوسط درجات الحرارة هو
المتوسط = \(11=\frac{55}{5}=\frac{14+10+12+9+10}{5}\)
بالتالي القيمة المتوسطة لدرجة الحرارة خلال الأسبوع المدرسي كانت °11, بما أن °11 هي قيمة قريبة جدا لجميع للقِيَم الأخرى التي قمنا بقياسها، يمكننا أن نقول أن المتوسط الذي توصلنا إليه هو مقياس تقريبي جيد لدرجات الحرارة في أيام الأسبوع.
الوسيط
إذا قمنا بترتيب جميع القِيَم حسب حجمها أو مقدارها ثم اخترنا القيمة التي تقع في منتصف القِيَم بعد ترتيبها، فإن القيمة الواقعة في المنتصف هي ما نسميه الوسيط. معرفة الوسيط مهمة و يُستحسن استخدامه عندما تكون قِيَم المجموعة مختلفة كثيرا و فيها بعض القِيَم بعيدة عن بعضها البعض.
سنرى الآن مثال، حيث أن الوسيط يعطي فكرة عن قِيَم المجموعة بصورة أفضل من الوسط الحسابي:
اشترت مُنى كتاب جديد به 210 صفحة، قرأت هذا الكتاب في سبعة أيام. في اليوم الأول قرأت 34 صفحة، في اليوم الثاني قرأت 40 صفحة، في اليوم الثالث قرأت 36 صفحة، في اليوم الرابع قرأت 31 صفحة، في اليوم الخامس قرأت 33 صفحة، في اليوم السادس قرأت 32 صفحة و في اليوم السابع قرأت الأربع صفحات المتبقية. نريد معرفة قيمة تقريبية واحدة لعدد الصفحات التي قرأتها مُنى في اليوم.
لإيجاد الوسيط في هذا المثال يمكننا ترتيب هذه القِيَم من الأصغر الى الأكبر كما يلي:
\(40,\,36,\,34,\,33,\,32,\,31,\,4\)
الآن نلاحظ مباشرة أن قيمة المنتصف هي 33, وهي الوسيط. في هذه الحالة لدينا من إجمالي السبع قِيَم ثلاث قِيَم أقل من الوسيط و ثلاث قِيَم أكبر من الوسيط.
في هذا المثال نلاحظ أن إيجاد الوسيط كان بسيط و سهل, لأنه كان لدينا عدد فردي من القِيم أي أنها كانت 7 قِيَم. لكن إذا كان لدينا عدد زوجي من القِيَم، على سبيل المثال 6 قِيَم، عندئذ لا توجد قيمة تقع في المنتصف. في هذه الحالة نحسب متوسط القيمتين الأقرب إلى المنتصف.
إذا قمنا بحساب المتوسط بدلا من حساب الوسيط لعدد الصفحات التي قرأتها منى في اليوم، سنحصل على:
المتوسط = \(30=\frac{210}{7}=\frac{34+40+36+31+33+32+4}{7}\)
توصلنا إلى أن منى قرأت بمُعدل 30 صفحة في اليوم. ولكن لأن منى قرأت أكثر من 30 صفحة في اليوم ما عدا اليوم الأخير، يمكن ملاحظة أن هذا المتوسط يعطي قيمة مضللة لعدد الصفحات التي قرأتها مُنى في اليوم. ولأن مُني قرأت في اليوم الأخير أربع صفحات فقط كان المتوسط أقل من المُتوقع. لهذا فإن الوسيط لا يعطي نفس إحساس الوسط الحسابي في حالة القيم التي تختلف اختلاف كبير عن بعضها البعض.
عائلة بها أربع أخوة أعمارهم 1 سنة, 3 سنوات, 5 سنوات و 13 سنة. احسب المتوسط و الوسيط لعمر الأطفال
نستخدم صيغة حساب المتوسط التالية:

\(5,5=\frac{22}{4}=\frac{13+5+3+1}{4}=\)
إذن متوسط عمر الأطفال هو 5,5 سنوات.
الآن نحسب الوسيط. أعمار الأطفال مُرتبة من الأصغر للأكبر ولكن لأن عدد الأطفال عدد زوجي (4 أطفال)، سنحسب الوسيط كمتوسط القيمتين الأقرب للمنتصف و هما 3 و 5. إذن سنحصل على الوسيط كما يلي:
الوسيط = \(4=\frac{8}{2}=\frac{5+3}{2}\)
الوسيط لعمر الأطفال هو 4 سنوات.
