جمع و طرح الكسور
الآن مررنا على كيفية كتابة الأعداد في صورة كسرية و كيف يمكننا اختصار أو مضاعفة الكسور.
في هذا القسم سندرس كيف يمكننا جمع أو طرح أعداد مكتوبة في صورة كسرية. عملية جمع و طرح الكسور الاعتيادية يمكن أن نسميها توحيد المقام.
جمع الكسور ذات المقام المشترك
كلما تم تقسيم شيء ما إلى أجزاء متساوية كلما كان كل جزء أصغر من الكل. هذا قد يسبب لنا بعض المشاكل مع جمع أو طرح الكسور الاعتيادية، على سبيل المثال نلاحظ أن 1\3 أكبر من 1\4.
إذا نظرنا أولا إلى الكسور الاعتيادية ذات المقام المشترك، أي أن مقاماتها لها نفس القيمة، سنلاحظ أنها سهلة الجمع, ولأن المقامات متساوية يمكننا مقارنة الكسور بسهولة.
في هذه الحالة نكتب المجموع في صورة الكسر المشترك بجمع بسطي الكسور و نترك مقامهم المشترك كما هو.
كمثال على هذا لدينا كسرين اعتياديين لهما مقام مشترك وهو 5, بحيث يمكن جمعهما مباشرة
\(\frac{2}{5}+\frac{1}{5}\) 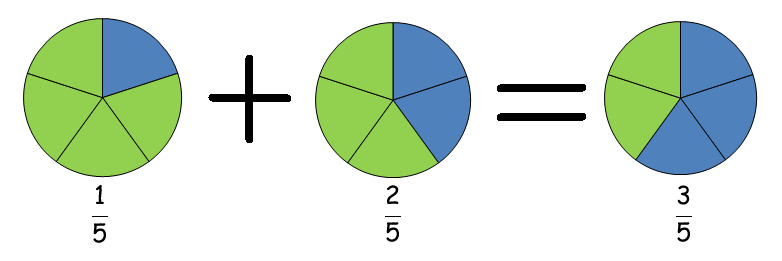
نحسب مجموع هذين الكسرين الاعتياديين كما يلي:
\(\frac{3}{5}=\frac{2+1}{5}=\frac{2}{5}+\frac{1}{5}\)
في هذا المثال كان من السهل جمع العددين الكسريين لأن لهما نفس المقام.
طرح الكسور ذات المقام المشترك
بنفس الطريقة التي اتبعناها عند جمع الكسور الاعتيادية ذات المقام المشترك يمكننا طرحها. في هذه الحالة نكتب إشارة الطرح وذلك بطرح البسطين من بعضهما و نترك مقاهما المشترك كما هو.
هنا لدينا مثال لطرح الكسور العادية ذات المقام المشترك:
\(\frac{1}{5}=\frac{2-3}{5}=\frac{2}{5}-\frac{3}{5}\)
احسب قيم التعبيرات التالية
أجب في أبسط صورة.
1) \(\frac{2}{7}+\frac{4}{7}\)
نرى أن الحدين لهما مقام مشترك وهو (7). هذا يعني أننا يمكن أن نحسب المجموع عن طريق جمع البسطين (4 و 2) و ترك المقام دون تغيير. لذا سنحصل على ما يلي:
\(\frac{6}{7}=\frac{2+4}{7}=\frac{2}{7}+\frac{4}{7}\)
مجموع 4\7 و 2\7 هو 6\7: لا يمكننا كتابة 6\7 في صورة أبسط من ذلك، لذا لقد أنجزنا المهمة.
2) \(\frac{3}{6}-\frac{5}{6}\)
في هذا المثال الحدين لهما مقام مشترك وهو (6). لذا يمكننا طرحهما بطرح البسطين (5 و 3) و ترك مقاهما المشترك دون تغيير. نحصل على الفارق التالي:
\(\frac{2}{6}=\frac{3-5}{6}=\frac{3}{6}-\frac{5}{6}\)
الفارق بين 5\6 و 3\6 هو 2\6:
هل الكسر 2\6 في أبسط صورة له؟ لا ليس في أبسط صورة لأنه يمكننا قسمة كل من البسط (2) و المقام (6) على 2. إذن سنختصر الكسر بالعدد 2, مما يعطينا ما يلي:
\(\frac{1}{3}=\frac{\,\,\frac{2}{{\color{Red} 2}}\,\,}{\frac{6}{{\color{Red} 2}}}=\frac{2}{6}\)
ما توصلنا إليه الآن هو الفارق مكتوب في أبسط صورة وهو 1\3. الفارق بين 5\6 و 3\6 هو 1\3:
جمع الكسور ذات المقامات المختلفة
ماذا نفعل إذا أردنا جمع كسور ذات مقامات مختلفة؟
إذا كان للكسرين مقامين مختلفين، نعيد كتابتهما حتى يكون لديهما مقام مشترك.
لإعادة كتابة الكسور في صورة مقام مشترك، نستخدم الاختصار و المضاعفة.
على سبيل المثال يمكننا حساب حاصل جمع الكسرين التاليين:
\(\frac{1}{3}+\frac{1}{4}\)
نلاحظ أن الحدين لهما مقامين مختلفين: الحد الأول مقامه 4 و الحد الثاني مقامه 3. لذا نحتاج إلى إعادة كتابة الكسور, بحيث يكون لهما مقام واحد مشترك.
أسهل طريقة للحصول على مقام مشترك لكسرين هو ضرب مقامي الكسرين في بعضهما. ومن ثم يصبح حاصل ضرب المقامين هو المقام الجديد:
\(12=3×4\)
لذا نريد إعادة كتابة الكسرين بحيث يكتبان كأجزاء من اثنى عشر (أي مقامهما 12) بدلا من الرُبع و الثُلث. الربع هو نفسه ثلاثة علــى أثني عشر، أي سنضاعف الكسر 1\4 بضرب بسطه و مقامه فــي 3 لنحصل على:
\(\frac{3}{12}=\frac{{\color{Red} {3×}}1}{{\color{Red} {3×}}4}=\frac{1}{4}\)
الآن، نعيد كتابة 1\4 ليصبح 3\12.
بنفس الطريقة نفعل ذلك مع الثُلث، لكن نضاعفه بالضرب في 4 لأن:
\(12=4×3\)
يمكن مضاعفة 1\3 بضرب بسطه و مقامه في 4 كما يلي:
\(\frac{4}{12}=\frac{{\color{Red} {4×}}1}{{\color{Red} {4×}}3}=\frac{1}{3}\)
الآن، نعيد كتابة 1\3 ليصبح 4\12.
ولأن الكسرين أصبح لهما مقام واحد مشترك وهو (12).
\(\frac{4}{12}+\frac{3}{12}=\frac{1}{3}+\frac{1}{4}\)
لذا يمكننا الآن حساب مجموعهما بجمع البسطين. يكون المجموع هو
\(\frac{7}{12}=\frac{4+3}{12}=\frac{3}{12}+\frac{4}{12}\)
حاصل جمع 1\4 و 1\3 هو 7\12 وهي أبسط صورة.
طرح الكسور ذات المقامات المختلفة
بنفس الطريقة التي اتبعناها عند جمع كسرين ذات مقامين مختلفين، سنحتاج إلى إعادة كتابة الكسور لإجراء عملية طرح كسور ذات مقامات مختلفة.
على سبيل المثال سنقوم بحساب الفرق بين الكسرين التاليين:
\(\frac{2}{3}-\frac{4}{5}\)
أولا, نعيد كتابة الكسرين بحيث يكون لدينا مقام مشترك. المقام المشترك في هذه الحالة هو 15, لأن حاصل ضرب مقامي الحدين (5 و 3) هو 15:
\(15=3×5\)
عندما نحصل على المقام المشترك المطلوب، نعيد كتابة الكسرين بحيث يكون مقامهما واحد وهو خمسة عشر. نضاعف الحد الأول بضرب البسط و المقام فــي 3 بحيث يصبح المقام 15. إذن سنحصل على:
\(\frac{12}{15}=\frac{{\color{Red}{3×}}4}{{\color{Red} {3×}}5}=\frac{4}{5}\)
بالتالي 4\5 يمكننا أن نكتبه 12\15:
نضاعف الحد الثاني بضرب البسط و المقام فـي 5 بحيث يصبح المقام 15. إذن سنحصل:
\(\frac{10}{15}=\frac{{\color{Red}{5×}}2}{{\color{Red} {5×}}3}=\frac{2}{3}\)
الآن نعرف أنه يمكننا كتابة 10\15 بدلا من 2\3 و لهما نفس القيمة.
الآن بعد توحيد المقام للكسرين يمكننا طرحهما كما يلي:
\(\frac{2}{15}=\frac{10-12}{15}=\frac{10}{15}-\frac{12}{15}=\frac{2}{3}-\frac{4}{5}\)
إذن ما توصلنا إليه الآن هو الفرق بين 4\5 و 2\3 وهو يساوي 2\15.
احسب قيم التعبيرات التالية
أجب في أبسط صورة.
1) \(\frac{2}{5}+\frac{1}{6}\)
بما أن الحدين لها مقامين مختلفين (6 و 5)، نقوم بإعادة كتابة الكسرين بمقام مشترك. هذا المقام المشترك هو
\(30=5×6\)
لذا سنضاعف الكسر 1\6 بضرب بسطه و مقامه فــي 5 و الكسر 2\5 بضرب بسطه و مقامه فــي 6 لنحصل على:
\(\frac{5}{30}=\frac{{\color{Red} {5×}}1}{{\color{Red} {5×}}6}=\frac{1}{6}\)
\(\frac{12}{30}=\frac{{\color{Red} {6×}}2}{{\color{Red} {6×}}5}=\frac{2}{5}\)
الآن يمكننا كتابة مجموع الكسرين على النحو التالي:
\(\frac{12}{30}+\frac{5}{30}=\frac{2}{5}+\frac{1}{6}\)
إذا حسبنا هذا المجموع سنحصل على
\(\frac{17}{30}=\frac{12+5}{30}=\frac{12}{30}+\frac{5}{30}\)
توصلنا الآن إلى أن مجموع 1\6 و 2\5 يساوي 17\30. هذا الكسر لا يمكن اختصاره أكثر من ذلك, لهذا انتهت العملية الحسابية.
2) \(\frac{1}{6}-\frac{2}{3}\)
نلاحظ أن الحدين لهما مقامين مختلفين (3 و 6)، لذا نحتاج إلى إعادة كتابتهما بحيث يكون لهما مقام واحد مشترك قبل أن نقوم بطرحهما.
في هذه الحالة لا نحتاج إلى مضاعفة الحدين، لأنه يمكننا ببساطة مضاعفة الحد الأول بحيث يكتب في شكل أسداس أي أن مقامه 6. وذلك من خلال مضاعفته بضرب البسط و المقام فــي 2:
\(\frac{4}{6}=\frac{{\color{Red}{2×}}2}{{\color{Red} {2×}}3}=\frac{2}{3}\)
الآن كلا الحدين مكتوبين كأسداس. لذا يمكننا طرحهما:
\(\frac{3}{6}=\frac{1-4}{6}=\frac{1}{6}-\frac{4}{6}=\frac{1}{6}-\frac{2}{3}\)
3\6 ليست مكتوبة في أبسط صورها لأن كل من البسط و المقام يمكن قسمتهما علــى 3. إذن سنختصر الكسر 3\6 بقسمة البسط و المقام علــي 3 لنحصل على:
\(\frac{1}{2}=\frac{\,\,\frac{3}{{\color{Red} 3}}\,\,}{\frac{6}{{\color{Red} 3}}}=\frac{3}{6}\)
بالتالي وصلنا الآن إلى أن حاصل طرح 2\3 و1\6 هو 1\2 وهي أبسط صورة.
(إذا لاحظنا أنه لا يمكن إعادة كتابة 2\3 كأسداس، يمكننا ضرب المقامين 3 و 6 للحصول على مقام مشترك وهو 18, وهذا يعني أنه يمكننا كتابة الحدين في شكل أجزاء من ثمانية عشر أي مقاماتهما 18. ولكن ستكون الإجابة كما هي في أبسط صوره لها وهي 1\2).
فيديو الدرس (بالسويدية)
في هذا الفيديو نشاهد أكثر عن جمع و طرح الأعداد الكسرية باستخدام الاختصارات و المضاعفات.
