الأعداد السالبة
في الفصول الدراسية السابقة تعلمنا الأعداد الطبيعية و الأعداد العشرية.
في هذا القسم سندرس الأعداد الأقل من الصفر: الأعداد السالبة. و سنبدأ باستعراض كيفية عمل الأعداد الطبيعية و الأعداد العشرية.
الأعداد الطبيعية و الأعداد العشرية
عندما نريد وصف عدد أو كمية شيء ما، على سبيل المثال يوجد 24 طالبا في الفصل أو كتاب ما يحتوي على 45 صفحة، في هذه الحالة نستخدم عادة الأعداد الطبيعية. الأعداد الطبيعية هي أعداد صحيحة لها قيم موجبة و تبدأ من الصفر.
الأعداد الطبيعية: \(...\,,3\,,2\,,1\,,0\)
يمكننا توضيح الأعداد الطبيعية على خط الأعداد:
![]()
أيضا استخدمنا الأعداد العشرية وهي أعداد صحيحة تحتوي على كسور عشرية، تتكون من أعشار، أجزاء من مائة، أجزاء من ألف وهكذا. وفيما يلي ثلاثة أمثلة على الأعداد العشرية
\(1,3\)
\(5,47\)
\(0,861476\)
لمن يريد تكرار كيفية عمل هذه الأنواع من الأعداد يمكنك قراءة المزيد في قسم الأعداد الطبيعية و الأعداد العشرية.
الأعداد السالبة
الآن سندرس الأعداد السالبة وهي الأعداد الأقل من الصفر. يُكتب العدد السالب بنفس طريقة العدد الموجب و لكن أمامه علامة ناقص (-). هناك أعداد صحيحة سالبة و أعداد عشرية سالبة، لكن في هذا الفصل سندرس أولا الأعداد الصحيحة السالبة.
مثال على استخدام الأعداد السالبة هو الدرجات السالبة على الثيرمومتر العادي (الذي يوضح درجات الحرارة بوحدة الدرجة المئوية أو سيلزيوس). الدرجات السالبة على الثيرمومتر هي أقل من درجة الصفر (°0 سيلزيوس). على سبيل المثال يمكننا باستخدام الثيرمومتر قراءة درجة الحرارة -°8 سيلزيوس وهي أقل من °0 سيلزيوس بــ °8 سيلزيوس.
الأعداد السالبة على خط الأعداد
على خط الأعداد تكون الأعداد السالبة يسار الصفر:
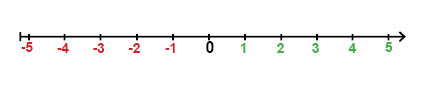
إذا نظرنا إلى خط الأعداد نلاحظ على سبيل المثال أن المسافة من الصفر الى العدد السالب -1 مساوية للمسافة من الصفر الى العدد الموجب 1, المسافة من الصفر الى العدد السالب -2 هي نفس المسافة من الصفر الى العدد الموجب 2 وهكذا.
عند اجراء الجمع و الطرح مع الأعداد السالبة هناك بعض الأشياء التي ينبغي أن نأخذها في الاعتبار. عندما نجمع (نضيف) أعداد موجبة سنتحرك يمينا على طول خط الأعداد. عندما نطرح أعداد موجبة سنتحرك يسارا على طول خط الأعداد.
للتعامل مع الأعداد السالبة يمكن أن يساعدنا التفكير في كيفية عملها على الثيرمومتر، عند زيادة أو انخفاض درجة الحرارة.
دعونا ننظر إلى هذا مثال
\(1=4+3-\)
يمكن أن نفهم عملية الجمع هذه بالنظر إلى خط الأعداد. نبدأ من العدد السالب -3 ثم نتحرك أربع خطوات تجاه اليمين، لأننا نريد إضافة العدد الموجب (4). في هذه الحالة سننتهي عند العدد الموجب 1.
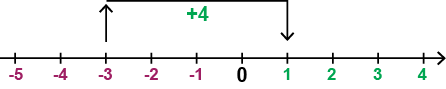
إذا فكرنا في هذه العملية الحسابية على الثيرمومتر الحراري، يمكن أن نتخيل أن درجة الحرارة كانت -°3 درجة مئوية (C) و ارتفعت درجة الحرارة بمقدار 4 درجات، مما يعطينا درجة حرارة جديدة وهي +°1 درجة مئوية (C).
بنفس الطريقة يمكننا معرفة ماذا يحدث عندما نطرح عدد موجب، مثلا
\(5-=2-3-\)
إذا نظرنا إلى خط الأعداد يمكن قراءة هذه العملية الحسابية، بحيث نبدأ من العدد السالب -3 ثم نتحرك خطوتين تجاه اليسار، وذلك لطرح العدد الموجب (2). في هذه الحالة سننتهي عند العدد السالب -5.
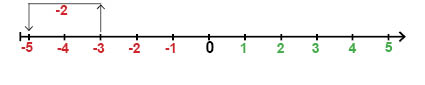
إذا فكرنا في هذه العملية الحسابية على الثيرمومتر، يمكننا أن نتخيل أن درجة الحرارة كانت -°3 درجة مئوية (C) و انخفضت درجة الحرارة بمقدار درجتين، مما يعطينا درجة حرارة جديدة وهي -°5 درجة مئوية (C).
إضافة الأعداد السالبة
الآن رأينا ماذا يحدث عندما يكون لدينا عدد سالب و نريد أن نضيف اليه أو نطرح منه عدد موجب. نضيف اليه العدد الموجب بالتحرك يمينا على طول خط الأعداد. و نطرح منه العدد الموجب بالتحرك يسارا على طول خط الأعداد.
لكن ماذا سيحدث إذا أضفنا عدد سالب؟ هذا ما سندرسه الآن.
إضافة عددين الى بعضهما تعني حساب قيمة مجموعهما معا. بما أن الأعداد السالبة أقل من الصفر، يمكن أن ننظر اليها كخَصم أو دَيْن. على سبيل المثال إذا كان لدينا 100 كرونة في البنك و علينا ديون بقيمة 50 كرونة، عندئذ لا يكون لدينا سوى 50 كرونة فقط لاستخدامها. هذا ما سيحدث عند إضافة الأعداد السالبة:
\(50=50-100=(50-)+100\)
عملية إضافة العدد -50 هي نفس عملية طرح العدد 50.
يمكن فهمها كما يلي: إذا كان لدينا 100 كرونة و علينا دين 50 كرونة، بالتالي لدينا فقط 50 كرونة متبقية. هذا هو نفس الشيء عندما يكون لدينا 100 كرونة واشترينا شيئا ما (طرحنا) بمبلغ 50 كرونة. في كلا الحالتين سيتبقى معنا 50 كرونة.
بنفس الطريقة عندما يكون لدينا عددين سالبين. على سبيل المثال إذا جمعنا العددين -100 و -50, سنحصل على:
\(150-=50-100-=(50-)+100-\)
هذا يمكن أن يكون على سبيل المثال علينا دَيْن 100 كرونة ثم زاد هذا الدَيْن بمقدار 50 كرونة. بالتالي سيكون اجملي الدَيْن (المطلوب) -150 كرونة.
طرح الأعداد السالبة
أيضا نريد أن نعرف ماذا سيحدث عندما نطرح الأعداد السالبة.
عملية الطرح تعني ما مقدار الاختلاف أو الفرق بين عددين. إذا كان لدينا عدد موجب وطرحنا منه عدد سالب سيكون الفرق أكبر مما إذا طرحنا عدد موجب.
كمثال على ذلك يمكن أن نتصور طائرة على ارتفاع 100 متر فوق سطح البحر و توجد غواصة بحرية على مسافة 50 متر تحت سطح البحر (عُمق الماء). المسافة الرأسية بين الطائرة والغواصة هي 150 متر، وهذا لأنه لدينا أولا 100 متر من الطائرة إلى سطح الماء زائدا 50 متر أخرى من سطح الماء الى الغواصة في الأسفل. هذه المسافة يمكن أن ننظر اليها كالفرق بين ارتفاع الطائرة فوق سطح الماء و بُعد الغواصة عن سطح الماء في الأسفل (الذي يعتبر سالب لأن الغواصة تحت سطح الماء). هذا باعتبار أن سطح الماء هو الصفر:
\(150=50+100=(50-)-100\)
عملية طرح العدد -50 هي نفس عملية أضافة العدد 50.
