الدوائر
في الأقسام السابقة الزوايا ونوعين من الأشكال الهندسية المألوفة: رُباعيات الأضلاع و المُثَلَّثات (ثُلاثيات الأضلاع)
في هذا القسم سندرس نوع هام من الأشكال الهندسية وهو الدائرة. كما سنتعلم أيضا كيفية وصف الدائرة، وما هو العدد بآي (pi), وكيف يمكننا حساب محيط و مساحة الدائرة.
القطر ونصف القطر
الدائرة هي شكل هندسي مستدير يبدأ من نقطة مركزية تسمى مركز الدائرة. على بُعد مسافة ما من مركز الدائرة يوجد ما يُسمى بمحيط الدائرة، وهو عبارة عن المنحنى الدائري الذي يشكل الدائرة. تُسمى المسافة من المركز إلى محيط الدائرة بنصف القطر (r), وله نفس الطول بغض النظر عن النقطة التي نختارها على المحيط.
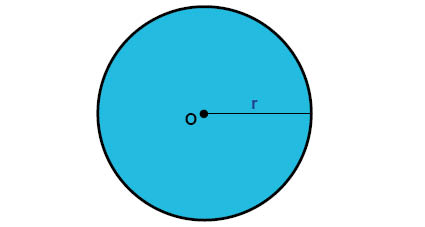
الخط المستقيم الذي يمر بين نقطتين على محيط دائرة و في الوقت نفسه يمر بمركز الدائرة يُسمى قطر الدائرة (d).
في الشكل أدناه تم توضيح كل من نصف القطر r, والقطر d.
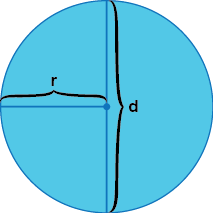
قطر الدائرة دائما ضعف نصف قطر الدائرة.
\(2r=d\)
محيط الدائرة والعدد بآي (pi), \(\pi\)
عندما درسنا محيط الأشكال الرُباعية الأضلاع والمثلثات توصلنا إلى أن محيط هذه الأشكال يساوي مجموع أضلاعها.
ولكن ليس من السهل حساب محيط الدائرة. إذا قمنا بقياس محيط وقطر دوائر متنوعة، سنلاحظ أننا في كل مرة نحصل على نفس خارج قسمة محيط الدائرة "O" على قُطر الدائرة "d".
خارج القسمة هذا هو نفس الناتج لجميع الدوائر وله القيمة التقريبية 3,14159265 عندما نقرب إلى أقرب ثماني أرقام عشرية. هذا العدد مهم جدا في علم الرياضيات ويُطلق عليه العدد بآي (pi) وهو مأخوذ من الحرف الإغريقي \(\pi\). بالتالي خارج قسمة محيط الدائرة علـى قطرها هو
![]()
باستخدام تعريف العدد بآي \(\pi\) يمكننا كتابة صيغة رياضية لمحيط الدائرة O:
المُحيط = \(\cdot \pi\) القُطر
\(d\cdot \pi=O\)
ولأن قطر الدائرة d يكون دائما ضعف نصف القطر r, يمكننا كتابة صيغة لمحيط الدائرة باستخدام (بدلالة) نصف القطر كما يلي:
المُحيط = \(\cdot\pi\cdot 2\) نصف القُطر
\(2\pi r=O\)
ما مقدار كل من القطر والمحيط؟
دائرة نصف قطرها 4 سم.
احسب قطر ومحيط الدائرة. قَرِب إلى رقم عشري واحد.
الحل:
بما أن قطر الدائرة ضعف نصف قطرها. إذن قطر الدائرة هو 8 سم.
نحسب الآن محيط الدائرة وفقا للصيغة التالية:
O = \(d \cdot \pi\) = \(8\cdot \pi\) سم = \(\pi 8\) سم \(\approx\) 25,1 سم
إذن القطر هو 8 سم والمحيط 25,1 سم تقريبا.
مساحة الدائرة
سنتعلم الآن كيفية حساب مساحة الدائرة.
إذا كان لدينا دائرة نصف قطرها r, و وضعناها داخل مربع سنحصل على الشكل التالي:
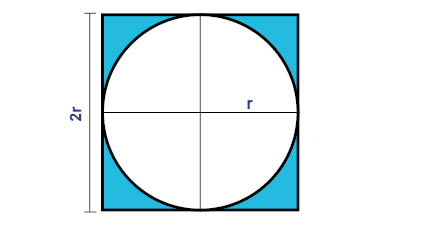
كما نعلم من قسم رُباعي الأضلاع سنحسب مساحة المربع على النحو التالي:
A_المربع = الضلع \(\cdot\) الضلع = \(4r^2=r\cdot r\cdot 4=2r\cdot 2r\)
يمكن أن نلاحظ أن هذا المربع يحتوي على أربعة مربعات صغيرة متساوية و طول ضلع كل منها r. كما نرى في الشكل مساحة الدائرة يجب أن تكون أصغر من مساحة المربع الكبير.
في الواقع مساحة الدائرة أكبر بقليل من ثلاث أضعاف مساحة أحد المربعات الصغيرة، كما هو موضح في الشكل. وبشكل أكثر تحديدا مساحة الدائرة أكبر من مساحة أحد المربعات الصغيرة بــ \(\pi\) مرة (3,14 مرة).
مساحة المربع = الضلع × الضلع
عليه فإن مساحة الدائرة ستكون:
A_الدائرة = \(\pi {r}^{2}=r\cdot r\cdot \pi\)
يمكننا استخدام صيغة مساحة الدائرة هذه لجميع الدوائر. لأن العدد \(\pi\) في كل الحالات له نفس القيمة (عدد ثابت), تعتمد مساحة الدائرة على نصف قطر الدائرة فقط.
مساحة الدائرة
دائرة نصف قطرها 4 سم.
احسب مساحة الدائرة. قرب إلى رقم عشري واحد.
الحل:
نستخدم صيغة مساحة الدائرة:
A = \({r}^{2}\cdot \pi\) = \({4}^{2}\cdot \pi\) سم2 = \(\pi 16\) سم2 \(\approx \) 50,3 سم2
إذن مساحة الدائرة تساوي 50,3 سم2 تقريباً.
قطاع الدائرة
في الصف السابع في قسم الزوايا خلصنا إلى أن الدورة الكاملة تعادل °360.
وقد نريد في بعض الأحيان دراسة أجزاء من الدائرة الكاملة، كشكل شرائح التورتة مثلا، كما في الشكل أدناه:
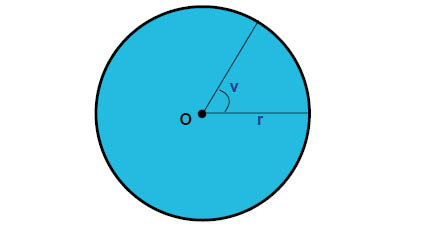
هذا النوع من أجزاء الدائرة (شكل شريحة التورتة) يُسمى قطاع الدائرة. ويعتمد حجم قطاع الدائرة على الزاوية الموجودة في منتصف الدائرة والتي نسميها الزاوية المركزية.
ويمكننا كتابة صيغة لمساحة قطاع الدائرة حيث يُشار إلى الزاوية المركزية بالحرف v:
A_قطاع الدائرة = \(\pi {r}^{2}\cdot \frac{v}{{360}^{\circ}}\)
إذا أردنا على سبيل المثال حساب مساحة قطاع دائري له زاوية مركزية \(v=90°\), سنحصل على مساحته باستخدام هذه الصيغة:
A_قطاع الدائرة = \(\pi {r}^{2}\cdot \frac{1}{4}=\pi {r}^{2}\cdot \frac{{90}^{\circ}}{{360}^{\circ}}\)
ما توصلنا إليه هو أن قطاع الدائرة الذي له زاوية مركزية v = 90° تكون مساحته ربع مساحة الدائرة. وهذا أيضا يمكننا الوصول إليه من خلال أن °90 تُمثل ربع دورة.
كم المساحة؟
دائرة نصف قطرها 10 سم. داخل الدائرة يوجد قطاع دائري زاويته المركزية °60.
احسب مساحة قطاع الدائرة. قرب إلى رقم عشري واحد.
ما هي النسبة التي تمثلها مساحة القطاع من المساحة الكلية للدائرة؟
الحل:
نعلم كل من نصف قطر الدائرة والزاوية المركزية لقطاع الدائرة. إذن يمكننا حساب المساحة باستخدام صيغة مساحة قطاع الدائرة.
A_قطاع الدائرة = \(\color{Red}{10^{2}}\ \cdot {\color{Red} {\pi \cdot {\color{Blue}{ \frac{60^{\circ}}{360^{\circ}}}}}}\) سم2 =
= \({\color{Red} {100\cdot\pi}}\cdot {\color{Blue}{ \frac{1}{6}}}\) سم2 \(\approx\) 52,3 سم2
إذن مساحة قطاع الدائرة هي 52,3 سم2 تقريباً.
الزاوية المركزية °60 تُشكل سُدس زاوية الدورة الكاملة (°360). وهذا يعني أن مساحة هذا القطاع تُشكل سُدس مساحة الدائرة الكاملة.
