النسبة, الجزء و الكل
في القسم السابق كررنا تعريف النسبة المئوية وكتابة الأعداد في صورة كسرية، صورة عشرية أو نسبة مئوية. كما تعلمنا أيضا في الصف السابع كيف يمكننا استخدام العلاقة بين النسبة، الجزء والكل لحساب النسبة المئوية لجزء معين.
في هذا القسم سنكرر العلاقة بين النسبة، الجزء والكل، كما سنستخدم هذه العلاقة لإيجاد مقدار كل من النسبة، الجزء أو الكل.
العلاقة بين النسبة، الجزء والكل
عندما نريد حساب النسبة المئوية لشيء ما, نقوم بقسمة مقدار الجزء على مقدار الكل.
على سبيل المثال إذا كان هناك 20 طالبا في الفصل، منهم 8 من البنات، يمكننا حساب أن البنات يمثلن %40 من إجمالي الطلاب:
\(0,4=40\,\%=\frac{40}{100}=\frac{8\,\cdot{\color{Blue}5}}{20\, \cdot{\color{Blue}5}}=\frac{8}{20}\)
في هذا المثال استخدمنا مضاعفة الكسر لتسهيل إجراء العملية الحسابية.
عندما نقوم بهذا النوع من العمليات الحسابية, عندها سنستخدم العلاقة بين النسبة, الجزء والكل.
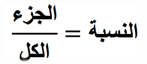
في مثال عدد الطالبات في الفصل، كانت النسبة 0.4 (%40), كان الجزء عبارة عن 8 طالبات وكان الكل 20 طالب بالفصل. بالنسبة نعني مقدار أو كمية جزء معين من الكل، في هذه الحالة يمكن تحديد مقدار الــ 8 طالبات من أصل 20 طالب في صورة عشرية أو نسبة مئوية.
حساب النسبة
الآن سنستخدم العلاقة بين النسبة، الجزء والكل لحساب النسبة المئوية لشيء ما من الكل.
أسقط لينوس طبق بيض
كان لينوس في متجر بقالة واشترى صندوق بيض يحتوي على 12 بيضة. في طريقه إلى المنزل أسقط لينوس صندوق البيض على الأرض وانكسرت تسع من البيض.
ما هي نسبة المئوية للبيض الذي لم ينكسر؟
الحل:
سوف نستخدم العلاقة بين النسبة، الجزء والكل، لذا سنبدأ بمعرفة كل من النسبة، الجزء والكل.
الكل هو عدد البيض الذي كان موجودا من البداية, أي 12 بيضة.
الجزء هو عدد البيض الذي لم ينكسر, أي 3 بيضات.
نسبة البيض الذي لم ينكسر يمكننا حسابها على النحو التالي:

\(=\frac{\frac{3}{{\color{Red} 3}}}{\frac{12}{{\color{Red} 3}}}=\frac{3}{12}=\)
\(25\,\%=0,25=\frac{1}{4}=\)
بالتالي نسبة البيض الذي لم ينكسر هي %25.
الانتخابات البلدية
في احدى الانتخابات البلدية حصل أحد الأحزاب السياسية على \(1\,000\) صوت. إجمالي الأصوات في الانتخابات \(20\,000\) شخص.
ما نسبة الأصوات المئوية التي حصل عليها هذا الحزب في الانتخابات؟
الحل:
الجزء هو ما نريد حساب نسبته وهو 1000 صوت.
الكل هو عدد الأصوات الكلي, أي \(20\,000\) صوت.
لإيجاد النسبة المئوية لعدد الأصوات التي حصل عليها الحزب، نحسب النسبة:

\(5\,\%=0,05=\frac{5}{100}=\frac{10}{200}=\frac{1\,000}{20\,000}=\)
إذن حصل الحزب على %5 من الأصوات في الانتخابات.
حساب الجزء
في بعض الأحيان نعلم ما هو الكل وما هي نسبة جزء معين من الكل, ونريد معرفة مقدار هذا الجزء. في مثل هذه الحالة يمكننا اعادة كتابة العلاقة بين النسبة، الجزء والكل باستخدام حَل المعادلة كما تعلمنا في الباب السابق:

بالتالي سنحصل على المعادله أدناه وهي التي يمكننا استخدامها لحساب الجزء:
الجزء = النسبة \(\cdot\) الكل
عندما نحسب بهذه الصيغة يجب أن نتذكر أن النسبة يجب أن تُكتب في صورة عشرية وليس نسبة مئوية. إذا كان لدينا على سبيل المثال النسبة %25 فهذا يعني أننا سنستخدم 0,25 (أي %25 في صورة عدد عشري) عندما نجري العملية الحسابية.
إذا أردنا معرفة النسبة %25 من 300 شخص، يمكننا حسابها كالآتي:
الجزء = النسبة \(\cdot\) الكل =
\(=300\cdot 25\,\%=\)
\(75=300\cdot 0,25=\)
بالتالي %25 من الـ 300 شخص هي 75 شخصا.
هناك طريقة لتسهيل هذا النوع من العملية الحسابية إذا استخدمنا الحساب العقلي، وهي حساب مقدار الــ %1 من الــ 300 أولا، ثم نضرب هذا المقدار فـي 25 للحصول على الجزء الذي يُمثل %25.
الجزء = النسبة \(\cdot\) الكل =
\(=300\cdot 25\,\%=\)
\(=300\cdot 1\,\%\cdot 25=\)
\(=300\cdot 0,01\cdot 25=\)
\(75=3\cdot 25=\)
بنفس الطريقة التي استخدمناها في هذا المثال يمكننا حساب حالات أخرى لمعرفة مقدار الجزء، إذا علمنا النسبة والكل.
تخفيض سعر جاكيت
كان يباع الجاكيت في متجر الملابس بسعر 600 كرونة في البداية. ثم انخفض السعر بنسبة %20.
ما مقدار التخفيض في السعر بالكرونة؟
الحل:
كان سعر الجاكيت في البداية 600 كرونة، لذا يمكننا أن نعتبرها الكل.
انخفض السعر بــ %20, بالتالي نسبة التخفيض في السعر هي 0,2 (%20).
إذن التخفيض في السعر بالكرونة هو
الجزء = النسبة \(\cdot\) الكل =
\(=600\cdot 20\,\%=\)
\(=600\cdot 0,2=\)
\(=600\cdot 0,1\cdot 2=\)
\(120=60\cdot 2=\) كرونة
إذن انخفاض السعر بنسبة %20 يعادل 120 كرونة.
إيجار ليزا و ماريا
تعيش ليزا وماريا معا في شقة طلاب. واتفقا على أن تدفع ليزا %60 من قيمة الإيجار وتدفع ماريا باقي الإيجار.
إذا كان الإيجار \(3\,000\) كرونة شهريا، كم ستدفع ليزا في الشهر؟
الحل:
ستدفع ليزا %60 من قيمة الإيجار، لذا النسبة التي سنستخدمها في الحساب هي 0,6 (%60).
الإيجار الكلي هو \(3\,000\) كرونة, إذن الكل هو \(3\,000\) كرونة.
بالتالي يمكننا الحصول على الجزء الذي ستدفعه ليزا من الايجار كما يلي:
الجزء = النسبة \(\cdot\) الكل =
\(=3\,000\cdot 60\,\%=\)
\(=3\,000\cdot 0,6=\)
\(=3\,000\cdot 0,1\cdot 6=\)
\(1\,800=300\cdot 6=\) كرونة
إذن الجزء الذي ستدفعه ليزا من الاجار هو 1800 كرونة شهريا.
حساب الكل
الطريقة الثالثة لاستخدام العلاقة بين النسبة، الجزء والكل هي حســاب الكل. وذلك باستخدام هذه النسخة من العلاقة:

أيضا في هذه الحالة يجب كتابة النسبة في صورتها العشرية، على سبيل المثال %25 ستصبح 0,25.
إذا كان %25 من مجموعة من الأشخاص هي 75 شخصا, يمكننا حساب عدد أشخاص المجموعة الكلي على النحو التالي:

\(=\frac{75}{0,25}=\)
\(=\frac{75\, \cdot\,{\color{Blue} 4}}{0,25\, \cdot\,{\color{Blue} 4}}=\)
\(300=\frac{300}{1}=\) شخص
إذا كان 75 شخصا يُمثلون %25 فإن عدد أشخاص المجموعة الكلي هو 300 شخص.
بنفس الطريقة التي استخدمناها في هذا المثال يمكننا حساب حالات أخرى لمعرفة الكل، إذا علمنا كل من الجزء والنسبة.
دخل ليزا
تدفع ليزا \(1\,800\) كرونة شهريا في إيجار شقة الطلاب التي تشارك فيها ماريا. ما تدفعه ليزا شهريا هو عبارة عن %30 من دخلها الشهري.
ما هو دخل ليزا؟
الحل:
يمكننا استخدام العلاقة بين النسبة، الجزء والكل لحساب دخل ليزا.
يُمثل إيجارها الشهري نسبة %30 من دخلها، إذن النسبة هي 0,3 (%30).
جزء من دخلها يذهب في الإيجار الشهري وهو \(1\,800\) شهريا، إذن الجزء هو \(1\,800\) كرونة.
بالتالي يمكنا حساب دخل ليزا على النحو التالي:

\(=\frac{1\,800}{0,3}=\)
\(=\frac{1\,800\, \cdot\,{\color{Blue} {10}}}{0,3\, \cdot\,{\color{Blue} {10}}}=\)
\(6\,000=\frac{18\,000}{3}=\) كرونة
إذن, دخل ليزا هو \(6\,000\) كرونة شهريا.
تخفيض ألعاب الكمبيوتر
اشترى بونتوس لعبة كمبيوتر في فترة التخفيضات وحصل على اللعبة بسعر أرخص من السعر السابق بمقدار 70 كرونة.
كم تكلفة اللعبة قبل التخفيض إذا كان تخفيض السعر %40؟
الحل:
نعلم أن التخفيض في السعر هو %40 من السعر قبل التخفيض، إذن النسبة هي 0,4 (40%).
التخفيض في السعر يعادل 70 كرونة، إذن الجزء هو 70 كرونة.
بالتالي يمكننا حساب سعر اللعبة قبل التخفيض على النحو التالي:

\(=\frac{70}{0,4}=\)
\(=\frac{70\, \cdot\,{\color{Blue}{ 10}}}{0,4\, \cdot\,{\color{Blue} {10}}}=\)
\(175=\frac{700}{4}=\) كرونة
فيديو الدرس (بالسويدية)
