المكعب و شبه المكعب

في القسم الخاص بالحجم ووحداته واجهنا واحد من أنواع الأشكال الهندسية الثلاثية الأبعاد وهو المكعب. وخلصنا إلى أن المكعب الذي طول ضلعه 1 متر، يكون حجمه 1 م\(^3\).

في هذا الفصل سنتعلم المزيد عن المكعب وشبه المكعب. وسنلاحظ أن المكعب هو في الحقيقة نوع من أنواع شبه المكعب.

المكعب وشبه المكعب

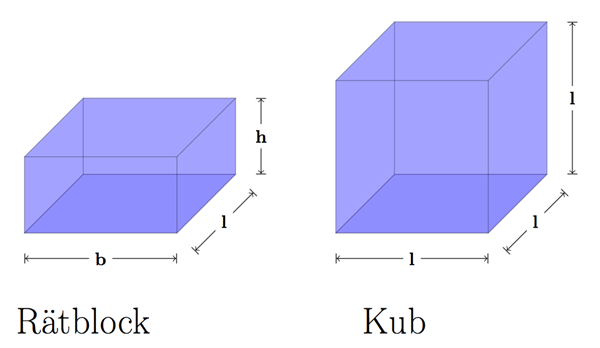
المكعب هو شكل ثلاثي الأبعاد متساوي الطول والعرض والارتفاع. جميع زوايا المكعب هي زوايا قائمة.

ومن أمثلة الأشياء التي لها شكل المكعب والتي قد تكون قابلتنا بالفعل هي النرد العادي ذو الستة أوجه أو الصندوق الذي يحتوي على ستة أوجه مربعة.

شبه المكعب هو شكل ثلاثي الأبعاد له طول وعرض وارتفاع مثل المكعب تماما، وجميع زواياه هي زوايا قائمة. ولكن طول وعرض وارتفاع شبه المكعب ليس بالضرورة أن يكون لهم نفس الطول كما في المكعب.

ومن أمثلة الأشياء التي لها شكل شبه مكعب حجر (لبنة) البناء أو صندوق الحذاء العادي.

اللغة السويدية	اللغة العربية
Kub	مكعب
Rätblock	شبه مكعب

جميع المكعبات أشباه مكعبات - المكعب هو ببساطة شبه مكعب جميع أوجهه متساوية في الطول. ولكن ليس جميع أشباه المكعبات مكعبات.

حجم المكعب أو شبه المكعب

لحساب حجم المكعب نبدأ بالنظر إلى الأضلاع التي تُشكل كل من طول المكعب (l) وعرض المكعب (b). الطول والعرض يُشكلان ما يُعرف بمساحة سطح القاعدة وشكلها شكل المستطيل. ثم نضرب مساحة سطح القاعدة هذه في ارتفاع المكعب (h) للحصول على حجم المكعب.

إذا كان المكعب في الشكل أعلاه طوله 4 سم وعرضه 4 سم وارتفاعه 2 سم, يمكننا حساب الحجم. أولا نحسب مساحة سطح القاعدة. ثم نضرب مساحة سطح القاعدة في الارتفاع للحصول على الحجم.

في الصف الثامن تعلمنا كيفية حساب مساحة المستطيل. بنفس الطريقة يمكننا حساب مساحة سطح القاعدة القاعدة (B):

مساحة سطح القاعدة = الطول \(\cdot\) العرض

\(b\cdot l=B\)

وبما أن ارتفاع المكعب 4 سم وعرضه 4 سم ستكون مساحة القاعدة 16 سم\(^2\):

\(B\) = 4 سم \(\cdot\) 4 سم = 16 سم\(^2\)

للحصول على الحجم نضرب مساحة سطح القاعدة فـي الارتفاع:

الحجم = مساحة القاعدة \(\cdot\) الإرتفاع

V_{شبه المكعب} = \(h\cdot B\)

فإذا كانت مساحة سطح القاعدة 16 سم\(^2\) والارتفاع 2 سم, إذن سيكون حجم المكعب 32 سم\(^3\):

V_{شبه المكعب} = \(h\cdot B\) = 16 سم\(^2\) \(\cdot\) 2 سم = 32 سم\(^3\)

إذا أردنا يمكننا أيضا كتابة حجم المكعب على النحو التالي:

الحجم = الطول \(\cdot\) العرض \(\cdot\) الإرتفاع

V_{شبه المكعب} = \(h\cdot b\cdot l\)

المكعب هو ببساطة شبه مكعب جميع أضلاعه متساوية في الطول. لذا يمكننا كتابة حجم المكعب بشكل أكثر سهولة. فإذا رمزنا إلى ضلع المكعب بالحرف \(l\) يمكننا أن نكتب حجمه على النحو التالي:

الحجم = الضلع \(\cdot\) الضلع \(\cdot\) الضلع

V_المكعب \({l}^{3}=l\cdot l\cdot l=\)

---

احسب حجم مكبر الصوت

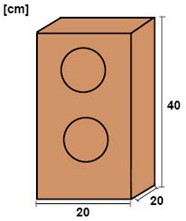
يبدو مكبر الصوت كما في الصورة التالية. حدد الحجم بوحدة سم\(^3\) وبوحدة اللتر.

الحل:

من الصورة نلاحظ أن مكبر الصوت يأخذ شكل شبه مكعب. شبه المكعب هذا طوله 20 سم وعرضه 20 سم وارتفاعه 40 سم.

يمكننا حساب حجم مكبر الصوت باستخدام صيغة حجم شبه المكعب على النحو التالي:

V_{مكبر الصوت} = \(h\cdot b\cdot l\) = 20 سم \(\cdot\) 20 سم \(\cdot\) 40 سم = \(16\,000\) سم\(^3\)

وسيكون من الجيد أيضا حساب مساحة القاعدة B أولا، ثم استخدامها مع الارتفاع h لحساب الحجم كما يلي

\(B\) = \(b\cdot l\) = 20 سم \(\cdot\) 20 سم = 400 سم\(^2\)

الآن لدينا مساحة القاعدة B, إذن يمكننا حساب الحجم بالطريقة التالية:

V_{مكبر الصوت} = \(h\cdot B\) = 400 سم\(^2\) \(\cdot\) 40 سم = \(16\,000\) سم\(^3\)

أي أن الحجم سيكون هو نفسه بغض النظر عن الطريقة المستخدمة.

الآن تم حساب الحجم بوحدة سم\(^3\)، ولكن نريد أيضا معرفة هذا الحجم بوحدة اللتر. من القسم الخاص بالحجم ووحداته نعلم أن

1 سم\(^3\) = 0,001 لتر

لذلك يمكننا إعادة كتابة هذا الحجم بوحدة اللتر على النحو التالي:

\(16\,000\) سم\(^3\) = \(\cdot 16\,000\) 0,001 لتر = 16 لتر

إذن حجم مكبر الصوت هو \(16\,000\) سم\(^3\)، وهو ما يعادل 16 لتر.

فيديوهات الدرس (باللغة السويدية)

حجم المُكعب.

حجم شِبه المُكعب.