الإحصاء

سابقا تعلمنا حساب المتوسط و الوسيط وكيف يمكننا استخدام الجداول والرسوم البيانية للحصول على نظرة شاملة لنتائج الدراسات الإحصائية.

في هذا القسم سنكرر كيفية استخدام الجداول التكرارية، كيف يمكننا حساب المتوسط والوسيط، وكيفية تفسير الرسوم البيانية.

الجداول التكرارية

أجرى فصل مدرسي به 10 تلاميذ اختبار يحتوي على ستة أسئلة.

عدد الأسئلة التي أجاب عليها كل طالب من الـ 10 طلاب بشكل صحيح هو:

\( 4,\,2,\,2,\,6,\,4,\,2,\,3,\,5,\,3,\,5 \)

للحصول على مفهوم أفضل عن نتائج الفصل يمكننا استخدام الجدول التكراري، وهو جدول تُدخل فيه عدد الإجابات الصحيحة وعدد الطلاب الذين أجابوا هذه الإجابات الصحيحة (التكرار).

بحيث يمكننا الحصول على الجدول التالي:

عدد الإجابات الصحيحة	عدد الطلاب (التكرار)
2	3
3	2
4	2
5	2
6	1

على سبيل المثال يمكننا أن نقرأ من الجدول التكراري أن هناك طالبان أجاب كل منهما على 4 أسئلة بطريقة صحيحة.

قد نريد أيضا حساب التكرار النسبي. التكرار النسبي في هذه الحالة يحدد نسبة الطلاب الذين لديهم عدد معين من الإجابات الصحيحة.

نوسع الجدول التكراري بحيث يحتوي أيضا على التكرار النسبي لكل إجابة من الإجابات الصحيحة:

عدد الإجابات الصحيحة	التكرار	التكرار النسبي
2	3	\(\frac{3}{10}\) =  % 30
3	2	\(\frac{2}{10}\) =  % 20
4	2	\(\frac{2}{10}\) =  % 20
5	2	\(\frac{2}{10}\) =  % 20
6	1	\(\frac{1}{10}\) =  % 10

المتوسط والوسيط

عندما يكون لدينا مجموعة من القِيّم غالبا ما نريد تلخيصها بطريقة معينة لتقدير مقاديرها بالتقريب. عندئذ نستخدم ما يُسمي بالمقاييس الموضعية. الآن نكرر اثنان‏ من المقاييس الموضعية الأكثر شيوعا: المتوسط والوسيط.

نحصل على المتوسط من خلال قسمة مجموع القِيّم علـى عدد القِيّم. عليه سنستخدم الصيغة التالية لحساب المتوسط:

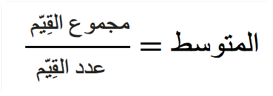
في المثال السابق أعلاه الخاص بعدد الإجابات الصحيحة في الاختبار المدرسي، يمكننا حساب متوسط عدد الإجابات الصحيحة على النحو التالي:

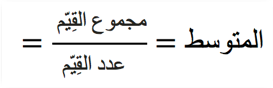
\(=\frac{1\cdot {\color{Magenta} 6}+2\cdot {\color{Magenta} 5}+2\cdot {\color{Magenta} 4}+2\cdot {\color{Magenta} 3}+3\cdot {\color{Magenta} 2}}{10}= \)

\(=\frac{6+10+8+6+6}{10}=\)

\(3,6=\frac{36}{10}=\)

إذن المتوسط هو 3,6 إجابة صحيحة. نقول أن الطلاب أجابوا بمعدل 3,6 سؤال بالإجابة الصحيحة.

نحصل على الوسيط من خلال ترتيب القِيّم حسب الحجم ونختار القيمة الواقعة في الوسط. إذا كان هناك عدد زوجي من القِيّم إذن لا توجد قيمة فردية تقع في المنتصف، بالتالي سنحسب الوسيط على أنه متوسط القيمتين الأقرب إلى المركز.

في المثال الخاص بعدد الإجابات الصحيحة في الاختبار المدرسي يمكننا تصنيف القِيّم على النحو التالي:

\( 6,\,5,\,5,\,4,\,4,\,3,\,3,\,2,\,2,\,2\)

بما أن عدد القِيّم زوجي (10 قِيّم)، سنحسب الوسيط على أنه متوسط العددين الواقعين في المنتصف.

\( 6,\,5,\,5,\,4,\,{\color{Red} 4},\,{\color{Red} 3},\,3,\,2,\,2,\,2\)

إذن الوسيط هو

الوسيط = \(3,5=\frac{7}{2}=\frac{4+3}{2}\)

تفسير الرسوم البيانية

تُستخدم الرسوم البيانية لإنشاء نظرة شاملة على القِيّم التي تم الوصول إليها في دراسة ما. سنتدرب الآن على تفسير الرسوم البيانية، وهو أمر من الجيد معرفته لأن المعلومات غالبا ما تُعرض في صورة رسوم بيانية.

---

درجات الحرارة من الاثنين الى الجمعة

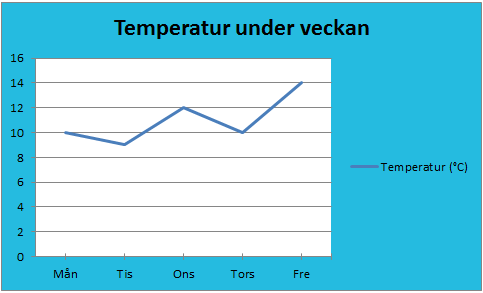
الرسم البياني الخطي التالي يوضح تقلب دراجات الحرارة على مدار خمسة أيام، من الاثنين إلى الجمعة.

اللغة السويدية	اللغة العربية
Temperatur under veckan	درجة الحرارة خلال الاسبوع
Temperatur	درجة الحرارة
C\(\circ \)	درجة مئوية (سلزيوس)
Mån \(\equiv\) Måndag	يوم الإثنين‏
Tis \(\equiv\) Tisdag	الثلاثاء‏
Ons \(\equiv\) Onsdag	الأربعاء‏
Tors \(\equiv\) Torsdag	الخميس‏
Fre \(\equiv\) Fredag	يوم الجمعة‏

فسّر الرسم البياني ثم احسب المتوسط والوسيط لدرجة الحرارة خلال الخمسة أيام

الحل:

من الرسم البياني نقرأ درجة حرارة الخمسة أيام بالسلزيوس (\(°C\)): 10, 9, 12, 10, 14.

بعد ذلك من السهل حساب المتوسط:

المتوسط = \(11=\frac{55}{5}=\frac{14+10+12+9+10}{5}\)

إذن المتوسط هو °11 سلزيوس.

لحساب الوسيط نرتب القِيّم حسب الحجم أي من الأصغر الى الأكبر: 9, 10, 10, 12, 14.

بما أنه لدينا عدد فردي من القِيّم (5 قيّم) فسيكون الوسيط هو القيمة الواقعة في المنتصف وهي °10 سلزيوس.

إذن المتوسط هو °11 سلزيوس والوسيط هو °10 سلزيوس.

---

زيارة السينما

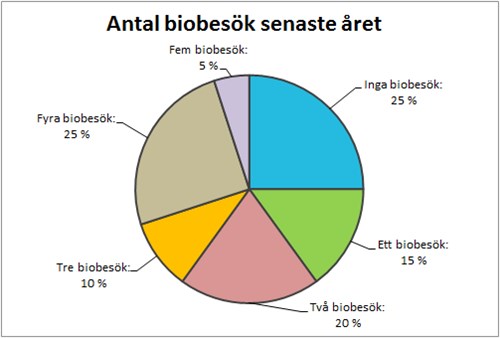
الرسم البياني الدائري أدناه يوضح نِسب عدد زيارات السينما لطلاب أحد الفصول الدراسية في السنة الماضية. يوجد في الفصل المدرسي 20 طالباً.

اللغة السويدية	اللغة العربية
Antal biobesök senaste året	عدد زيارات السينما في العام الماضي
Inga biobesök	لا توجد زيارة للسينما
Ett biobesök	زيارة واحدة للسينما
Två biobesök	زيارتين للسينما
Tre biobesök	ثلاث زيارات للسينما
Fyra biobesök	أربع زيارات للسينما
Fem biobesök	خمس زيارات للسينما

فسّر الرسم البياني واحسب المتوسط والوسيط لعدد زيارات السينما في السنة الماضية.

الحل:

من الرسم البياني يمكننا معرفة النسبة المئوية لعدد زيارات الطلاب المختلفة للسينما، وهذا هو ما يُعرف بالتكرار النسبي. بما أننا نعلم عدد الطلاب الكلي في الفصل (20)، يمكننا معرفة عدد الطلاب الذي يمثله كل جزء من الدائرة.

على سبيل المثال نقرأ أن %25 من الطلاب لم يذهبوا إلى السينما على الإطلاق في السنة الماضية، بالتالي عدد الطلاب الذي يعادل هذه النسبة هو

\( 5=20\cdot 0,25=20\cdot 25\,\%\)

بنفس الطريقة يمكننا معرفة عدد الطلاب الذين ذهبوا إلى السينما 0, 1, 2, 3, 4 و 5 مرات, ويمكننا أن كتابته كما في الجدول التكراري أدناه.

عدد زيارات السينما	التكرار النسبي	التكرار
0	% 25	5
1	% 15	3
2	% 20	4
3	% 10	2
4	% 25	5
5	% 5	1

الآن نعرف التكرار ويمكننا حساب المتوسط كما يلي:

المتوسط = \(=\frac{1\cdot {\color{Magenta} 5}+5\cdot {\color{Magenta} 4}+2\cdot {\color{Magenta} 3}+4\cdot {\color{Magenta} 2}+3\cdot {\color{Magenta} 1}+5\cdot {\color{Magenta} 0}}{20}\)

\(=\frac{5+20+6+8+3+0}{20}\)

\(2,1=\frac{42}{20}=\)

وهذا يعني أن متوسط عدد الزيارات للسينما في السنة الماضية هو 2,1 زيارة. أي أن الطلاب ذهبوا إلى السينما بمعدل 2,1 مرة على مدار السنة الماضية.

كيف نحسب الوسيط؟

قيمة الوسيط هي القيمة الواقعة في المنتصف ويمكننا اجادها بترتيب هذه القِيّم حسب مقدارها. بما أنه توجد 20 قيمة (20 طالبا), سنبحث عن القيمتين العاشرة والحادية عشر وذلك لحساب متوسطهما للحصول على الوسيط.

يمكننا إيجاد هذه القيمة باستخدام الجدول التكراري. القِيّم مرتبة حسب المقدار من الصغر للأكبر أي من الــ 0 الى الــ 5 , لكن الــ 0 متكرر خمس مرات و الــ 5 متكررة ثلاث مرات ما يعني أن الــ 0 و الــ 5 معا يمثلان الثماني قِيّم الأولى. بالتالي القِيّم التاسعة، العاشرة، الحادية عشر والثانية عشر توجد في الصف الثالث من الجدول التكراري، وهذا الصف يعرض عدد الطلاب الذين ذهبوا للسينما مرتين.

إذن الوسيط يساوي 2 أي زيارتين للسينما في السنة الماضية.

إذا وضعنا القيم العشرين مرتبة حسب مقدارها سنحصل على نفس القيمة للوسيط بالضبط.

فيديوهات الدرس (باللغة السويدية)

التكرار والتكرار النسبي.

المتوسط (القيمة المتوسطة).

المتوسط والجدول التكراري.

الوسيط.

المنوال.