النسبة، الجزء والكل
في الصفين السابع والثامن تعلمنا العلاقة بين النسبة والجزء والكل.
في هذا القسم سنكرر كيفية استخدام هذه العلاقة في مواقف مختلفة. لأننا سنحتاج لمعرفة استخدام هذه العلاقة عندما ندرس في القسم القادم الزيادات والانخفاضات, كما سنتعلم استخدام عوامل التغير عند حساب عدة زيادات أو تخفيضات متتالية.
النسبة, الجزء والكل
إذا كان لدينا 10 كُرات، أربع منها حمراء فمن ثم يمكننا حساب نسبة (النسبة المئوية) عدد الكُرات الحمراء على النحو التالي:

عندما نقوم بإجراء هذا النوع من العمليات الحسابية، في الواقع نستخدم صيغة معينة من العلاقة بين النسبة والجزء والكل؛ كالعلاقة التالية:

في مثالنا لعدد الكُرات الحمراء كان الجزء (4 كُرات)، وإجمالي عدد الكُرات كان يُمثل الكل (10 كُرات)، ونسبة الكُرات الحمراء هي بالطبع النسبة (%40).
يمكننا إعادة كتابة هذه العلاقة بين النسبة والجزء والكل بطريقتين آخرتين، بناء على ما نريد حسابه.
إذا أردنا معرفة مقدار الجزء الذي تُمثله نسبة معينة من الكل سنستخدم الصيغة التالية:
الجزء = النسبة \(\cdot\) الكل
إذا علمنا من جانب آخر نسبة جزء معين وأردنا معرفة مقدار الكل فسنستخدم الصيغة التالية:

نحسب الآن بعض الأمثلة نستخدم فيها هذه الصيغ.
حساب النسبة
إذا أردنا حساب نسبة جزء معين من الكل سنحتاج إلى معرفة مقدار الجزء ومقدار الكل حَسَب الصيغة التالية

درس ألعاب رياضية
في فصل يضم 25 طالبا، كان الطلاب يختارون أنشطة مختلفة أثناء درس الألعاب الرياضية. اختار 5 طلاب لعب كرة القدم، بينما اختار 12 طالبا لعب كرة الطائرة، واختار 8 طلاب لعب كرة السلة.
ماهي النسبة المئوية للطلاب الذين اختاروا كل نشاط من الأنشطة المختلفة؟
الحل:
بما أننا نريد معرفة النسبة المئوية (الجزء من مائة) للطلاب الذين اختاروا الأنشطة المختلفة، هذا يعني أننا نريد حساب النسبة.
ما هو الجزء؟ يختلف الجزء في الثلاث أنشطة المختلفة، لأن كل جزء حَسَب اختيار عدد معين من الطلاب. الكل هو متشابه في جميع الحالات، وهو 25 طالبا في الفصل الدراسي.
نبدأ بحساب النسبة المئوية للطلاب الذين لعبوا كرة قدم. كان عدد الطلاب الذين اختاروا كرة القدم 5 طلاب وهذا هو الجزء. إذن نحسب النسبة كما يلي:

\(20\,\%=0,2=\frac{1}{5}=\frac{5}{25}=\)
بالمثل يمكننا حساب النسبة المئوية للطلاب الذين لعبوا كرة طائرة، وهم 12 طالبا:

\(48\,\%=0,48=\frac{48}{100}=\frac{{\color{Blue} 4\,\cdot}\,12}{{\color{Blue} 4\,\cdot}\,25}=\frac{12}{25}=\)
لحساب نسبة الطلاب الذين لعبوا كرة سلة، يمكننا أن نسهل على أنفسنا ونستخدم ما قمنا بالفعل بحسابه، لأن نسبة الطلاب الكلية الذين شاركوا في كل من الثلاث أنشطة هي %100.
النسبة(سلة) = % 100 - النسبة(قدم) - النسبة(طائرة) =
\(32\,\%=48\,\%-20\,\%-100\,\%=\)
إذن %20 من الطلاب لعبوا كرة قدم, %48 لعبوا كرة طائرة و %32 لعبوا كرة سلة أثناء درس التربية البدنية.
حساب الجزء
لحساب الجزء سنحتاج إلى معرفة النسبة (نسبة الجزء) ومقدار الكل، حَسَب الصيغة التالية
الجزء = النسبة \(\cdot\) الكل
كم مقدار %25 من 320 كرونة؟
في هذه المهمة نعلم مقدار الكل وهو 320 كرونة. نعلم أيضا النسبة وهو %25 (ويجب أن نستخدمه في صورة كسر عشري 0,25).
مقدار الـ %25 من 320 كرونة هو الجزء الذي نبحث عنه، لذا نستخدم الصيغة التالية
الجزء = النسبة \(\cdot\) الكل = 0,25 \(\cdot\) 320 كرونة =
= \(\frac{1}{4}\) \(\cdot\) 320 كرونة = \(\frac{320}{4}\) كرونة = 80 كرونة
إذن %25 من الـ 320 كرونة هي 80 كرونة.
حساب الكل
إذا أردنا حساب الكل سنحتاج إلى معرفة جزء معين ونسبته، بموجب الصيغة التالية

إذا كان لديك 10 خرزات في يدك وتعلم أن هذا الخرز يمثل %40 من الخرز الذي تمتلكه، كم عدد الخرز الكلي الذي تمتلكه؟
نعلم أن %40 من الخرز تساوي 10 خرزات. لذا نسبة هذا الجزء من عدد الخرز الكلي هي %40 (0,4). الجزء هو الــ 10 خرزات التي سنبدأ منها حساب عدد الخرز الكلي.
لحساب عدد الخرز الكلي (الكل) سنستخدم الصيغة التالية
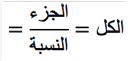
\(25=\frac{100}{4}=\frac{{\color{Blue} {10\,\cdot}}\, 10}{{\color{Blue} {10\,\cdot}}\, 0,4}=\frac{10}{0,4}=\)
إذن عدد الخرز الكلي هو 25 خرزة.
فيديوهات الدرس (بالسويدية)
في هذا الفيديو سنتعرف على كيفية حساب النسبة باستخدام العلاقة بين النسبة والجزء والكل.
في هذا الفيديو سنتعرف على كيفية حساب الجزء باستخدام العلاقة بين النسبة والجزء والكل.
في هذا الفيديو سنتعرف على كيفية حساب الكل باستخدام العلاقة بين النسبة والجزء والكل.
