الأهرامات

في القسم السابق تعلمنا المخاريط. المخروط هو شكل هندسي له قاعدة مُسطحة وغلاف مُسطح يتشكل من نقطة خارج القاعدة المُسطحة. عندما نتحدث عن المخاريط فإننا نعني المخاريط العادية التي لها قاعدة مُسطحة دائرية، وهي نوع من أنواع المخاريط التي تشبه قُمع الآيس كريم.

في هذا القسم سندرس الأهرامات وهي في الحقيقة نوع من أنواع المخاريط. توجد الأهرامات في عدة سياقات مختلفة، ولكن الأكثر شهرة هي أهرامات مصر، وهي هياكل كبيرة مبنية في شكل الأهرامات الصحيح.

الأهرامات

الهرم هو شكل هندسي له قاعدة مُسطحة متعددة الأضلاع كالمستطيل أو المثلث على سبيل المثال. أيضا الهرم له أسطح جانبية في شكل مثلثات تلتقي في نقطة عند رأسه.

الشكل التالي يوضح هرم له قاعدة مُسطحة B في شكل مثلث:

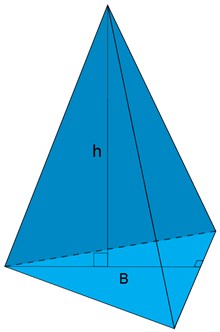
ارتفاع الهرم h هو المسافة العمودية بين سطح القاعدة ورأس الهرم.

جميع الأهرامات عبارة عن مخاريط لها سطح قاعدة مضلع.

حجم الهرم

بما أن الهرم هو نوع من أنواع المخروط، يمكننا استخدام نفس صيغة حجم المخروط لحساب حجم الهرم:

V_الهرم \(\frac{h\cdot B}{3}=\)

حجم المخروط الدائري المستقيم يساوي ثلُث حجم الأسطوانة التي لها نفس القاعدة المُسطحة والارتفاع. ولكن حجم الهرم يساوي ثُلث حجم المنشور الذي له نفس القاعدة المُسطحة والارتفاع.

---

احسب حجم الهرم

هرم ارتفاعه 5 أمتار وسطح قاعدته في شكل مستطيل عرضه 10 أمتار وطوله 18 متر، أحسب حجم الهرم.

الحل:

يمكننا حساب حجم الهرم بالصيغة المعروفة التالية

V_الهرم \(\frac{h\cdot B}{3}=\)

نحتاج إلى معرفة كل من مساحة سطح القاعدة B وارتفاع الهرم h.

نعلم أن مساحة قاعدة الهرم عبارة عن مستطيل عرضه 10 أمتار وطوله 18متر، وباستخدام صيغة مساحة المستطيل يمكننا حساب مساحة سطح القاعدة كما يلي

\(180=18\cdot 10=h\cdot b=B\) م\(^2\)

بما أننا نعلم ارتفاع الهرم وهو 5 أمتار، يمكننا الآن حساب حجم الهرم:

V_الهرم \(300=5\cdot 60=\frac{5\cdot 180}{3}=\frac{h\cdot B}{3}=\) متر\(^3\)

إذن حجم الهرم هو 300 متر\(^3\).

فيديو الدرس (باللغة السويدية)

حساب حجم الهرم.