الاحتمالات
في السابق تعلمنا كيف يمكننا كتابة الأعداد في صورة كسرية أو في صورة نسبة مئوية.
إمكانية كتابة الأعداد في هذه الصور سنستخدمها في هذا القسم، والآن سنتعلم كيفية حساب احتمال وقوع الأحداث المختلفة.
ما هو الاحتمال؟
في بعض الحالات لا نعلم ماذا سيحدث. ولكن أحيانا في مثل هذه الحالات يمكننا معرفة مدى الاحتمال أو فرصة حدوث حدث معين. هذا الجزء من الرياضيات الذي يَتَعَلَّق بالاحتمالات يُسمى نظرية الاحتمالات.
على سبيل المثال بالنسبة للذين يلعبون لعبة الحظ أو يا نصيب كما يسميها البعض، يمكننا معرفة مدى احتمال حصولهم على تذكرة رابحة إذا عرفنا كم عدد التذاكر الرابحة وكم عدد التذاكر الكلي.
إذا قمت بقذف قطعة عملة معدنية سوف لن تعلم أي الوجهين ستقف عليه - صورة أم كتابة. ولكن تعرف أنها ستقف إما على الصورة أو الكتابة. لذا نقول أنه يوجد نتيجتان محتملتان. ونعني بالنتيجة وقوع حدث معين. في هذه الحالة أيضا نعلم أن فرصة وقوف العملة على الصورة تساوي فرصة وقوفها على الكتابة.

بالتالي نقول أن احتمال وقوف العملة على الصورة على سبيل المثال يساوي %50 ويمكننا كتابته بطرق مختلفة:
\(\frac{1}{2}=0,5=50\,\%\)
واحتمال وقوف العملة على الكتابة هو نفسه يساوي %50.
ويشار عادة إلى احتمال وقوع حدث معين بالحرف P (الذي أتى من الكلمة الإنجليزية probability وتعني احتمال)
لذا يمكننا كتابة احتمال وقوف العملة على الصورة والكتابة كما يلي:
(الصورة)P \( 50\,\%=\)
(الكتابة)P \(50\,\%=\)
إذا كان هنالك احتمال متساوي لوقوع نتائج مختلفة فمن ثم يمكننا حساب احتمالية وقوع حدث معين بشكل عام كما يلي:

في مثال قذف العملة المعدنية يمكننا دراسة احتمالية الحصول على الكتابة. في هذه الحالة وجه الكتابة فقط هو النتيجة المطلوبة، لأنه هو الحدث الذي نهتم به. عدد النتائج الممكنة هو اثنان، لأنه يمكننا الحصول إما على الكتابة أو الصورة. لذا يمكننا حساب احتمال الحصول على الكتابة كما يلي:

وهو بالضبط نفس الاحتمال الذي وصلنا إليه أعلاه، ولكن تعريف الاحتمالات هذا مفيد جدا في المواقف الأكثر تعقيدا، كما سنرى لاحقا.
أحد السمات الأخرى للاحتمالات التي من الضروري معرفتها هو أن هنالك دائما احتمالان, احتمال حدوث شيء أواحتمال عدم حدوثه, فالاحتمالان معا دائما يساويان %100. مثلا عندما نقذف عملة معدنية سيكون لدينا احتمالان, احتمال الحصول على وجه الصورة أواحتمال عدم الحصول عليه, هاذان الإحتمالان دائما يساويان %100.
(الصورة)P + (غير الصورة)P \(100\,\%=1=\)
حساب الاحتمالات
بعد أن تعلمنا ما هو الاحتمال وكيف يمكننا حسابه سندرس بعض المواقف الأكثر تعقيدا.
إذا رمينا نرد طبيعي به ستة أوجه فما هو احتمال أن نحصل على الــ 3؟
نستخدم تعريف الاحتمال وهو النسبة بين عدد النتائج المطلوبة وعدد النتائج الممكنة. هناك نتيجة واحدة مطلوبة، لأننا نهتم فقط بالحالة التي يظهر فيها الرقم 3. لأن النرد له ست أوجه ولها نفس احتمال الحدوث عندما نرمي النرد، فهناك ست نتائج محتملة الحدوث.
لذلك يمكننا حساب احتمال الحصول على الــ 3 كما يلي:

إذن احتمال الحصول على 3 هو سُدس، أي حوالي %16,7.
ما مدى احتمال عدم الحصول على 3, عندما نرمي النرد؟
نستخدم أيضا في هذه المرة تعريف الاحتمال. في هذه الحالة النتيجة المطلوبة عدم ظهور الــ 3 عند رمي النرد، أي ظهور كل من 1, 2, 4, 5 أو 6. بمعنى أنه لدينا 5 نتائج مطلوبة. وما زال عدد النتائج الممكنة الكلي ست نتائج لأن النرد له ست أوجه.
لذلك يمكننا حساب احتمال عدم الحصول على 3 عندما نرمي النرد كما يلي:

أيضا نعلم أن احتمال وقوع الحدث أواحتمال عدم وقوعه دائما يساويان 1.
(\(3\))P + (غير الــ 3)P =
\(=\frac{5}{6}+\frac{1}{6}=\)
\(=\frac{5+1}{6}=\)
\(100\,\%=1=\frac{6}{6}=\)
إذا رميت نرد له ست أوجه، ما مدى احتمال الحصول على الــ 5 أو الــ 6؟
لحساب الاحتمالات نبدأ بدراسة النتيجة المطلوبة (المرغوب فيها).
في هذه الحالة النتيجة المطلوبة هي ظهور 5 أو 6 على النرد. إذن عدد النتائج المطلوبة هو 2.
ما هو عدد النتائج الممكنة الكلي؟ بما أن النرد له ست أوجه, إذن هنالك 6 نتائج يمكن حدوثها عندما نرمي النرد رمية واحدة.
لذا يمكننا حساب احتمال الحصول على 5 أو 6 على النحو التالي:

بالتالي احتمال الحصول على 5 أو 6 هو ثُلث أي حوالي %33,3.
إذا رميت نرد له ست أوجه، ما هو مدى احتمال الحصول على رقم زوجي أو 1؟
هنا الوضع معقد قليلا، ولكن يمكننا حساب الاحتمالات إذا قمنا أولا بدراسة جميع النتائج الممكنة وعدد النتائج المطلوبة.
النرد له ست أوجه لذا مجموع النتائج الممكنة الكلي هو 6 نتائج محتملة.
الأعداد الزوجية هي 2, 4 و 6. لذا النتائج المطلوبة هي 1, 2, 4 و 6, وهي 4 نتائج مطلوبة.
لذلك يمكننا حساب احتمال الحصول على رقم زوجي أو على الــ 1 على النحو التالي:
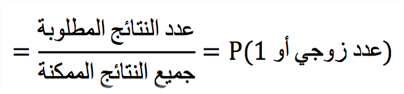
\(66,7\,\%\approx \frac{2}{3}=\frac{4}{6}=\)
إذن احتمال الحصول على رقم زوجي أو 1 هو ثُلثين، أي حوالي %66,7.
فيديوهات الدرس (باللغة السويدية)
مفهوم الإحتمال مع بعض الأمثلة باستخدام زهرات النرد.
هنا نواصل في مفهوم الإحتمالات مع زهرات النرد.
مفهوم الإحتمال.
