معادلة الخط المستقيم
في الكورسات رياضيات 1 ورياضيات 2 تعلمنا كيف يمكن استخدام كل من الدوال الخطية و معادلة الخط المستقيم. لنستعرض الآن كيف يمكن وصف العلاقات الخطية باستخدام معادلة الخط المستقيم.
نبدأ بمثال
إذا أراد شخص الإقامة في فندق لفترة معينه فكل ليلة يقضيها في الفندق ستكلف مبلغ مالي معين، لنفترض 500 كرونة. التكلفة الإجمالية للإقامة بالفندق ستعتمد على كل من تكلفة الليلة وعدد الليالي التي أقامها الشخص في الفندق. يمكن وصف هذه العلاقة كما يلي:
التكلفة الكلية = 500 كرونة \(\cdot\) عدد الليالي
إذا رمزنا لعدد الليالي بالحرف \(x\) والتكلفة الكلية بالحرف \(y\) فيمكننا صياغة هذه العلاقة كما يلي
$$y=500x$$
فإذا أراد الشخص استخدام منتجع الفندق مرة واحدة بالإضافة إلى تكلفة الأيام الكلية التي قضاها في الفندق، يمكن أن نفترض أن الرسوم الإضافية ستكون 250 كرونة. بالتالي يمكننا إعادة كتابة العلاقة كما يلي:
التكلفة الكلية = 500 كرونة \(\cdot\) عدد الليالي + 250 كرونة
$$y=500x+250$$
هذه المعادلة هي عبارة عن نموذج للمعادلة الخطية. وهذه هي المعادلة التقليدية التي تصف العلاقة بين المتغيرين \(x\) و \(y\). إذا رسمنا الدالة المقابلة \((y (x)=500x+250)\) على نظام إحداثيات سنحصل على خط مستقيم ولهذا تُسمى هذه المعادلة بمعادلة خط مستقيم.
سنرى ذلك بحساب قيّم \(y\) المقابلة لقيّم مختلفة للمتغير \(x\) ومن ثم تحديد عدد من النقاط الاحداثية (x, y) على نظام الإحداثيات ونوصل هذه النقاط ببعضها.
الجدول أدناه يوضح إجمالي التكلفة لثلاث حالات مختلفة (ليلتين, 3 ليالِ و5 ليالِ)
$$y(2)=500\cdot 2+250=1250$$
$$y(3)=500\cdot 3+250=1750$$
$$y(5)=500\cdot 5+250=2750$$
عندما نكتب \(y(2)\) فهذا يعني أن لدينا دالة \(y(x)\) ونبحث عن قيمة \(y\) عند \(x = 2\). بصورة عامة، عادة ما تُكتب:
$$y(x)=500x+250$$
أو
$$f(x)=500x+250$$
إذا أردنا بعد ذلك إدخال قيّم مختلفة للمتغير \(x\) وحساب قيمة الدالة المقابلة سنقوم بتعويض القيمة المختارة في جميع الأماكن التي يوجد بها المتغير \(x\) في تعبير الدالة.
إذا أردنا أن نكون أكثر وضوحا يمكننا أيضا كتابة:
$$y(x=2)=500\cdot 2+250$$
| عدد الليالي (x) | التكلفة الكلية (y) | إحداثيات (x,y) |
| 2 | 1250 | (2, 1250) |
| 3 | 1750 | (3, 1750) |
| 5 | 2750 | (5, 2750) |
الآن هذه النقاط التي تم إيجادها في الجدول أعلاه سيتم تحديدها على نظام الإحداثيات ومن ثم توصيلها ببعضها البعض لنرى ما إذا كان سنحصل على خط مستقيم. 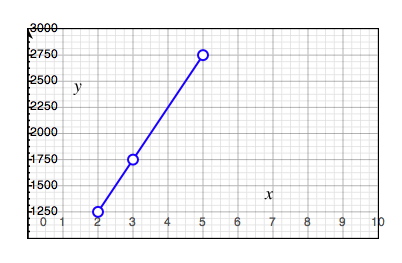
بناء على صيغة هذه الدالة يمكننا اختيار عدد لا نهائي من الأعداد الصحيحة الموجبة كقيّم للمتغير \(x\) (التي تُمثل عدد الليالي في هذه الحالة) وتعويضها في الدالة للحصول على قيّم \(y\) الفريدة (التي تُمثل إجمالي تكلفة الإقامة في الفندق) المقابلة لكل قيمة من قيّم المتغير \(x\). كل نقطة من هذه القيّم الزوجية من \(x\) و \(y\) ستقع على امتداد نفس الخط على نظام الإحداثيات. هذا الخط هو الذي يُمثل الدالة
$$y(x)=500x+250$$
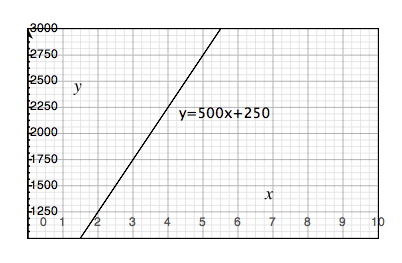
صيغة معادلة الخط المستقيم:
$$y=kx+m$$
جميع المعادلات التي تخضع لهذا النموذج ستُشكل خط مستقيم إذا أردنا وصف العلاقة على نظام الإحداثيات. يختلف شكل الخطوط المستقيمة على نظام الإحداثيات حسب الميل ونقطة التقاطع. يُرمز للميل بالحرف k الذي يُمثل معامل الميل. في المثال أعلاه قيمة k هي 500 وهذا يعني أن زيادة \(x\) بمقدار 1 يؤدي لزيادة \(y\) بمقدار 500 (كل ليلة إضافية تعني زيادة في التكلفة بمقدار 500 كرونة). يُرمز لنقطة التقاطع بالحرف m وهي عبارة عن الحد الثابت في المعادلة. m هي قيمة \(y\) التي يتقاطع عندها هذا الخط مع محور \(y\) وقيمة m في هذا المثال 250
في نظام الإحداثيات أدناه تم رسم علاقة خطية جديدة. يمكننا إيجاد معادلة هذا الخط المرسوم بدراسته على نظام الإحداثيات. بما أن هذا الخط مستقيم فهذا يعني أن معادلته ستكون في صيغة معادلة الخط المستقيم. مالا نعرفه حتى الآن هو قيمة k وقيمة m في هذه المعادلة. بمجرد تحديد قيمة k (معامل الميل) وقيمة m (الحد الثابت\الجزء المقطوع) لأي علاقة الخطية بالتالي لدينا الوصف الكامل لمعادلة الخط.
$$y=?x+?$$
سوف نبدأ بحساب ميل الخط، أي قيمة k.
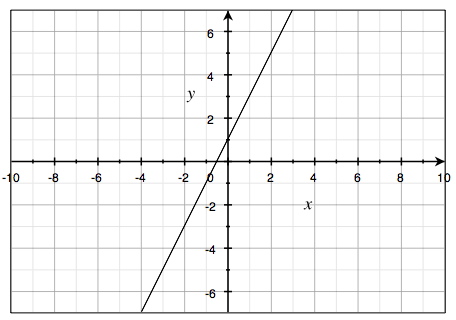
يتم حساب قيمة k باستخدام الصيغة التالية:
$$k=\frac{\bigtriangleup y}{\bigtriangleup x}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$$
يمكننا الحصول على قيمة k - مقدار ميلان الخط بأخذ أي نقطتين وحساب الفرق بين قيمتي إحداثيات \(y\) والقسمة علـى الفرق بين قيمتي إحداثيات \(x\). لنختار النقطتين (2, 5) و (1, 3).
سنعرض هاتان النقطتان في نظام الإحداثيات أدناه:
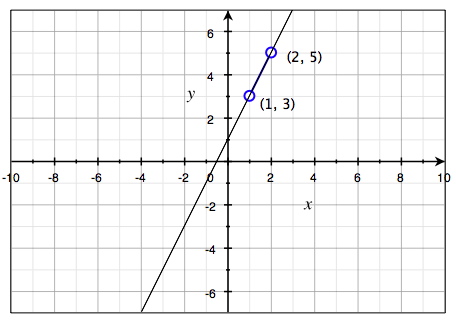
الفرق بين قيمتي إحداثيات \(y\):
$$\\y_{2}-y_{1}=5-3=2\\$$
الفرق بين قيمتي إحداثيات \(x\):
$$x_{2}-x_{1}=2-1=1$$
بالتالي قيمة k هي:
$$k=\frac{2}{1}=2$$
أخيرا سنحسب قيمة m وذلك من خلال قراءة نقطة تقاطع هذا الخط مع محور \(y\) وهي عند \(y=1\) وهي قيمة m.
$$m=1$$
الآن تم إيجاد قيّم الثوابت المجهولة في المعادلة. بالتالي يمكن وصف هذا الخط على نظام الإحداثيات بالمعادلة
$$y(x)=2x+1$$
الآن سنرسم دالة أخرى على نفس نظام الإحداثيات:
$$y(x)=2x$$
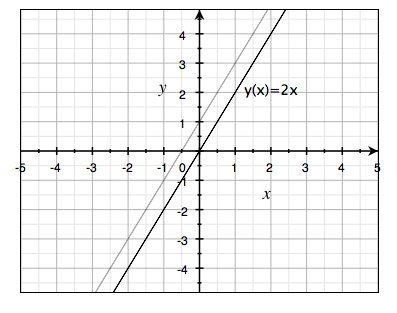
قيمة m في الدالة الجديدة تساوي صفر ويمكن ملاحظة ذلك على نظام الإحداثيات حيث أن خط هذه المعادلة يقطع محور \(y\) عند نقطة الأصل (\(y=0\)). لاحظ أن الدالتين متوازيتين. بما أن كلا الدالتين لهما نفس قيمة k \((k = 2)\) فهذا يعني أن لهما نفس الميل وهذا هو سبب عملية التوازي.
| أي خطان لهما نفس قيمة الميل- k متوازيان |
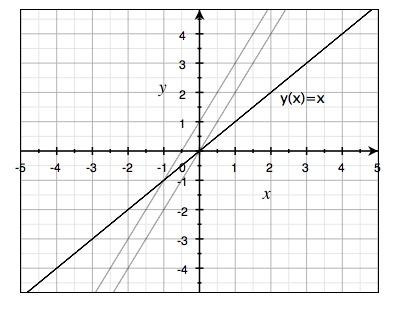
على نظام الإحداثيات التالي تم رسم دالة أخرى بالإضافة للدالتين السابقين
$$y(x)=x$$
هذه الدالة بسيطة ونلاحظ أن قيمة كل من k و m مختفيتين. معامل الميل هو معامل \(x\) وهو 1, والحد الثابت m يساوي صفر.
في المثال التالي تم رسم دالة رابعة على نفس نظام الإحداثيات:
$$y(x)=2$$
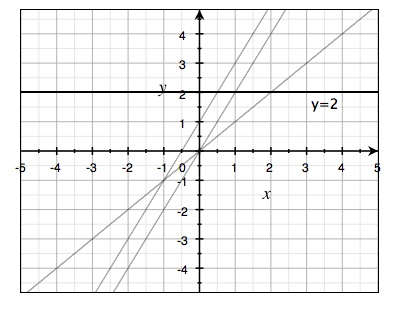
تعبير هذه الدالة لا يحتوي على قيمة لـ k لأنها تساوي صفرا؛ يحتوي على قيمة m فقط (m = 2).
كما نلاحظ أن خط هذه الدالة يقطع محور \(y\) عند \(y=2\). عندما تكون قيمة k صفر فستكون قيمة الدالة هي نفسها بغض النظر عن قيمة \(x\) ولهذا سيكون خط هذه الدالة أفقي، أي موازي لمحور \(x\).
أخيرا سنرسم دالة أخرى (الخط الأخضر) على نظام إحداثيات:
$$y(x)=-2x-3$$
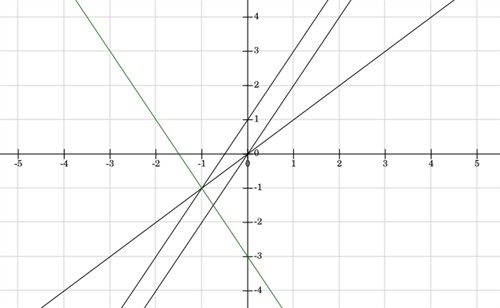
لاحظ أن قيمة كل من k و m لهذه الدالة عبارة عن قيّم سالبة. عندما تكون قيمة k سالبة، يكون الميل سالب ولهذا سيكون الخط ساقطا للأسفل (تتناقص \(y\) لكل زيادة في \(x\), في هذه الحالة ستتناقص \(y\) بمقدار 2 لكل زيادة في \(x\) بمقدار 1). عندما تكون قيمة m تساوي \(-3\) فهذا يعني أن الخط سيقطع محور \(y\) عند \(y = -3\) ويمكن ملاحظة ذلك على نظام الإحداثيات أعلاه.
| الخط الذي ميله موجب (\(k>0\)) سيكون تزايدي. الخط الذي ميله صفر (\(k=0\)) سيكون موازيا لمحور \(x\). الخط الذي ميله سالب (\(k<0\)) سيكون تناقصي. |
الخط الذي معادلته في الصيغة \(x = 2\) لا يمكن كتابة معادلته في صيغة معادلة الخط المستقيم أعلاه بينما سيكون خط مستقيم على نظام الإحداثيات ولكن ليس له ميل (قيمة k تساوي واحد صحيح) ولا يتقاطع مع محور \(y\) (m ليست لها قيمة):
$$x=2$$
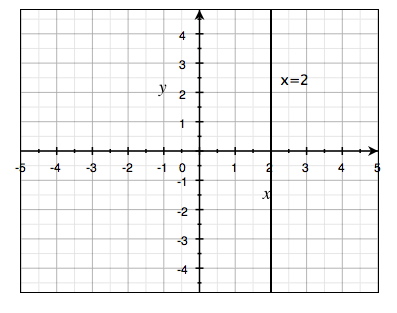
بما أن لدينا قيمة \(x\) فقط ولا يمكن تحديد قيمة \(y\) فهذا يعني أن الخط سيكون موازي لمحور \(y\).
| أي خط له معادلة مثل (\(x=2\)) لا يمكن كتابة معادلته في الصيغة (\(y=kx+m\)) وانما سيكون موازيا لمحور \(y\). |
فيديو الدرس
شرح الإحداثيات ومعادلة الخط المستقيم.
