قاعدة الجيب (جا)
في القسم السابق درسنا قاعدة مساحة المُثلث والتي يمكن استخدامها لحساب مساحة المثلث إذا علمنا أطوال ضلعين من أضلاع المُثلث ومقدار الزاوية المحصورة بينهما.
في هذا القسم سنتعلم قاعدة آخرى من قواعد المثلثات وهي قاعدة جيب الزاوية التي تصف العلاقة بين أضلاع المثلث وزواياه.
سنستخدم نفس المثلث الذي استخدمناه في القسم السابق:
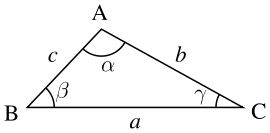
قاناون جيب الزاوية:
$$\frac{\sin \alpha}{a}=\frac{\sin \beta }{b}=\frac{\sin \gamma }{c}$$
يجب أن نتذكر أن \(a\) هو الضلع المقابل للزاوية \( \alpha \) كما في الشكل؛ بنفس الطريقة الضلع \(b\) هو الضلع المقابل للزاوية \(\beta\) والضلع \(c\) هو الضلع المقابل للزاوية \(\gamma\).
أما إذا كان لدينا طولي الضلعين \(a\) و \(b\) وإحدى الزاويتين \( \alpha \) أو \(\beta\), ففي هذه الحالة يمكننا إعادة كتابة قاعدة جيب الزاوية, بحيث يمكن حساب مقدار الزاوية المفقودة مباشرة:
مثلا إذا علمنا طول كل من الضلعين \(a\) و\(b\) ومقدار الزاوية \(\alpha \) ونريد معرفة الزاوية \(\beta\), ففي هذه الحالة يمكننا حساب \(\beta\) كما يلي:
$$sin \: \beta = {\frac{b\cdot sin \: \alpha}{a}}$$
$$\beta = sin^{-1} \left ( {\frac{b\cdot sin \: \alpha}{a}} \right )$$
بنفس الطريقة يمكننا إيجاد أطوال أحد أضلاع المُثلث الأخرى أو إحدى زواياه الأخرى وذلك بإعادة كتابة علاقة قاعدة الجيب.
لنأخذ مثال على ذلك
مثلث إحدى زواياه \(50°\) والضلع المقابل لها طوله 5 سم. فإذا كان طول الضلع الآخر للمثلث 4 سم ما مقدار الزاوية المقابلة للضلع الذي طوله 4 سم؟
إذا رمزنا للزاوية المعروفة بـ \(\alpha \) \((50°)\) والزاوية المجهولة بـ \(\beta\) والضلع الذي طوله 5 سم بــ \(a\) والذي طوله 4 سم بــ \(b\), ووفقاً قاعدة جيب الزاوية يمكن إستخدام العلاقة التالية:
$$\frac{sin \: 50^\circ}{5}=\frac{sin \: \beta}{4}$$
ويمكننا إعادة كتابة هذه المعادلة المثلثية كما يلي:
$$\beta = sin^{-1} \left ( {\frac{4\cdot sin \: 50^\circ}{5}} \right )\approx 37,8^\circ$$
فيديوهات الدرس
هنا سنشرح قاعدة جيب الزاوية.
إستخدام قاعدة جيب الزاوية لإيجاد قيّم الزوايا و أطوال الأضلاع في مُثلث ما.
