قاعدة جيب التمام (جتا)
في القسمين السابقين درسنا قاعدتين من قواعد المُثلثات: قاعدة مساحة المُثلث والتي يمكن استخدامها في حساب مساحة المُثلث, و قاعدة الجيب والتي تصف العلاقة بين إثنين من أضلاع المثلث والزوايا المقابلة لهاذين الضلعين.
في هذا القسم سنتعلم قاعدة مُثلثية ثالثة وهي قاعدة جيب تمام الزاوية والتي تصف العلاقة بين أضلاع المثلث الثلاثة وإحدى زوايا هذا المثلث.
باستخدام قاعدة جيب تمام الزاوية يمكننا حساب مقدار الزاوية إذا علمنا أطوال أضلاع المثلث الثلاثة، كما يمكننا أيضاً حساب طول أي ضلع إذا علمنا مقدار إحدى الزوايا وأطوال الضلعين الآخرين.
مرة أخرى سنستخدم نفس المثلث الذي استخدمناه في القسمين السابقين:
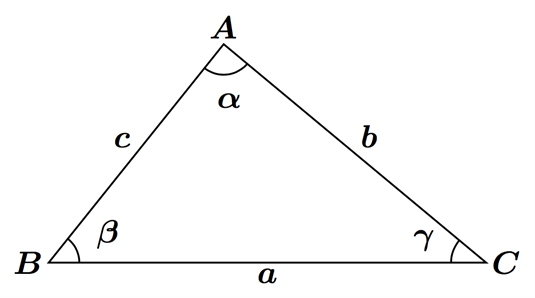
قاعدة جيب تمام الزاوية:
$$a^{2}=b^{2}+c^{2}-2bc\cdot \cos \alpha$$
توجد حالتين نموذجيتين لإستخدام قاعدة جيب تمام الزاوية: الحالة الأولى إذا علمنا أطوال أضلاع المُثلث الثلاثة ونريد معرفة مقدار زاوية مجهولة والحالة الثانية إذا علمنا أطوال ضلعين ومقدار زاوية واحدة (على الأقل) ونريد معرفة طول الضلع الثالث.
يمكن إعادة كتابة قاعدة جيب التمام بناءاً على ما نبحث عنه، بحيث يمكننا حساب ما هو مجهول.
دعونا نأخذ ثلاثة أمثلة على استخدام قاعدة جيب تمام الزاوية
مثال 1
في مثلث ما لدينا ضلع طوله 4 سم وضلع آخر طوله 10 سم ومقدار الزاوية المحصورة بينهما \(50°\). احسب طول الضلع المقابل للزاوية \(50°\).
نبدأ برسم المثلث كما يلي:
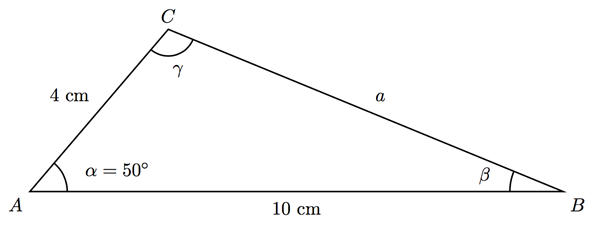
بإستخدام الشكل أعلاه وقاعدة جيب التمام يمكننا الحصول على:
$$a^2=4^2+10^2-2\cdot 4\cdot 10\cdot cos \: 50^\circ$$
$$a=\sqrt{4^2+10^2-2\cdot 4\cdot 10\cdot cos \: 50^\circ}\approx 8 \: cm$$
إذن طول الضلع المقابل للزاوية \(50°\) هو \( 8 \: cm\).
مثال 2
مُثلث أطوال أضلاعه: \( 5 \: cm\), \( 9 \: cm\) و \( 12 \: cm\). ليس لدينا معلومة عن أي زاوية. أحسب الزاوية المقابلة للضلع الذي طوله \( 12 \: cm\).
نبدأ برسم المثلث كما يلي:
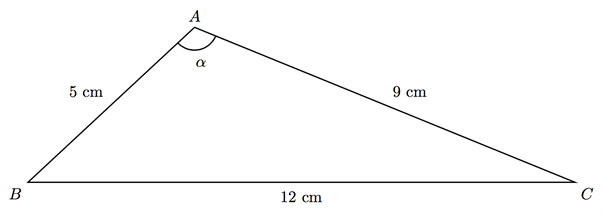
بإستخدام الشكل أعلاه وقاعدة جيب التمام يمكننا الحصول على:
$$12^2=9^2+5^2-2\cdot 9\cdot 5\cdot \cos \alpha$$
$$2\cdot 9\cdot 5\cdot \cos \alpha=9^2+5^2-12^2$$
$$\cos \alpha=\frac{9^2+5^2-12^2}{2\cdot 9\cdot 5}$$
$$\alpha=\arccos{\left( \frac{9^2+5^2-12^2}{2\cdot 9\cdot 5}\right) }$$
$$\alpha= 115^{\circ}$$
إذن الزاوية المقابلة للضلع \( 12 \: cm\) هي \(115°\).
مثال 3
مُثلث أطوال إثنين من أضلاعه \( 6 \: cm\) و \( 5 \: cm\). الزاوية المقابلة للضلع \( 5 \: cm\) مقدارها \(40°\).أحسب طول الضلع الثالث.
نبدأ برسم المثلث كما يلي::
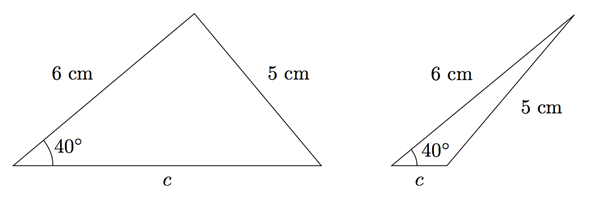
كما نلاحظ من الشكل أعلاه فإن الضلع المجهول يمكن أن يأخذ قيمتين.
بإستخدام الشكلين أعلاه وقاعدة جيب التمام يمكننا الحصول على: :
$$5^2=6^2+c^2-2\cdot 6\cdot c\cdot \cos 40^{\circ}$$
نبدأ بوضع جميع الحدود في طرف واحد:
$$0=c^2-2\cdot 6\cdot \cos 40^{\circ}\cdot c + 6^2-5^2$$
$$0=c^2-12\cdot \cos 40^{\circ}\cdot c + 11$$
يمكنن إستخدام ضيغة-pq لإيجاد قيمة c:
$$c= \frac{12\cdot \cos 40^{\circ}}{2} \pm \sqrt{\left( \frac{12\cdot \cos 40^{\circ}}{2} \right)^2 -11 }$$
$$c= 6\cdot \cos 40^{\circ} \pm \sqrt{36 (\cos 40^{\circ})^2 -11 }$$
ما يعطي أن:
$$c_1\approx 7,8 \: cm$$
$$c_2\approx 1,4 \: cm$$
إذن طول الضلع الثالث هو \(7,8 \:cm\) أو \(1,4 \:cm\) تقريباً.
فيديوهات الدرس
هنا سنشرح قاعدة جيب التمام (جتا).
إستخدام قاعدة جيب تمام الزاوية لإيجاد قيّم الزوايا و أطوال الأضلاع في مُثلث ما.
