الزيادة والنقصان

درسنا كيفية إيجاد مُشتقة الدوال عن طريق تعريف قاعدة الإشتقاق بإستخدام المسافة-h كما أوجدنا طُرق أخرى مُختصرة لإجاد هذه المُشتقات وذلك بإستخدام عدد من قواعد التفاضُل. الآن سنتعمق أكثر في دراسة الدوال ورسومها البيانية والعلاقة بين الدالة وميل المماس.

تختلف قيمة-k من مماس لآخر وتعتمد قيمة-k على كيفية ميل المماس على المنحنى.

دعونا ندرس دالة الدرجة الثانية البسيطة \(f (x) =x^2+1\) من خلال رسمها البياني التالي:

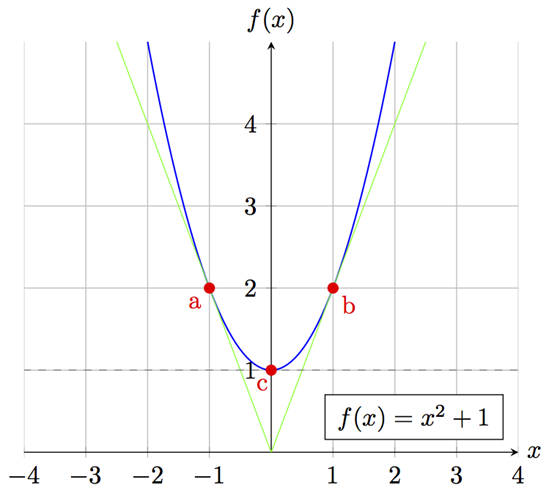
في الشكل أعلاه تم تعيين ثلاث نقاط على المنحنى: \(a\) وإحداثياتها \((-1, 2)\), \(b\) إحداثياتها \((1, 2)\) و \(c\) إحداثياتها \((0, 1)\).

عند النقطة \(a\) لدينا مماس متناقص. أيضاً قيمة-k لهذا المماس سالبة كما أنّ المُشتقة عند هذه النقطة أيضاً سالبة.

عندما تكون \(f '(x) < 0\) فسيكون المماس متناقصا عند النقطة \(x\).

من الشكل أيضا يمكن ملاحظة أن جميع النقاط على طول المنحنى حيث تقع قيمة \(x\) في المدى

$$-\infty <x<0$$

سيكون المماس عندها متناقص، أي أن المُشتقة ستكون سالبة عند جميع النقاط في هذا المدى، أي عند جميع النقاط على طول المنحنى الواقعة يسار النقطة \(c\) في الشكل.

تكون الدالة متناقصة في مدى معين لقيّم \(x\) \((a\leq x\leq b)\) إذا كان في هذا المدي لدينا أن \(x_{1} < x^{2}\) وتحصلنا على قيّم تناقصية للدالة, أي أن \(f(x_{1}) > f(x^{2})\). يمكننا أيضا أن نقول أن الدالة ستكون تناقصية في مدى معيّن إذا كان

$$ f'(x)<0$$

وينطبق هذا على جميع قيّم \(x\) في هذا المدى.

في هذا المثال كانت الدالة متناقصة في المدى

$$-\infty<x<0$$

وذلك لأن قيمة الدالة \(f (x)\) تتناقص باستمرار كلما زادت قيمة \(x\).

عند النقطة \(b\) لدينا مماس مُتزايد. أيضاً قيمة-k للمماس موجبة كما أنّ المُشتقة عند هذه النقطة موجبة.

عندما تكون \(f '(x) > 0\) فسيكون المماس متزايداّ عند النقطة \(x\).

بنفس الطريقة أعلاه يمكننا أيضا أن نلاحظ من الشكل أن جميع النقاط الواقعة على طول المنحنى حيث تقع قيمة \(x\) في المدى

$$ 0<x<\infty $$

سيكون المماس عندها متزايد، أي أن المُشتقة ستكون موجبة عند جميع النقاط في هذا المدى. أي عند جميع النقاط على طول المنحنى الواقعة يمين النقطة \(c\) في الشكل.

تكون الدالة متزايدة في مدى معين لقيّم \(x\)

$$ a\leq x\leq b $$

تكون الدالة متزايدة في مدى معين لقيّم \(x\) \((a\leq x\leq b)\) إذا كان في هذا المدي لدينا أن \(x_{1} > x^{2}\) وتحصلنا على قيّم تزايدية للدالة, أي أن \(f(x_{1}) < f(x^{2})\). يمكننا أيضا أن نقول أن الدالة ستكون تزايدية في مدى معيّن إذا كان

$$f'(x)>0$$

وينطبق هذا على جميع قيّم \(x\) في هذا المدى.

في هذا المثال كانت الدالة متزايدة في المدى

$$ 0<x<\infty $$

وذلك لأن قيمة الدالة \(f (x)\) تتزايد باستمرار كلما زادت قيمة \(x\).

عند النقطة \(c\) لدينا مماس أفقي (موازي لمحور \(x\), أي ميله يساوي صفر) وقيمة-k في هذه الحالة تساوي صفر ما يعني أن قيمة الُمشتقة في هذه النقطة أيضاً تساوي الصفر.

عندما تكون \(f '(x) = 0\) فهذا يعني أن المماس لا ميل له.

فيديوهات الدرس

في هذا الفيديو سنشرح مفهوم الدوال المتزايدة والدوال المتناقصة.

هنا سنواصل في شرح الدوال التزايدية والتناقصية ومتى ستكون تزايدية أو تناقصية.

كيف يمكننا أن نتفرف على نوع الدالة, تزايدية أم تناقصية.