الدوال النسبية
في القسم السابق درسنا التعبيرات النسبية وهي عبارة عن عملية قسمة بين متعددتي حدود. الآن دعونا نرى ماذا سيحدث إذا أدخلنا مثل هذه التعبيرات النسبية في دالة، وهذا ما يُسمى بالدالة النسبية.
فيما يلي مثال على دالة نسبية
$$f(x)=\frac{x^{2}}{x-1}$$
على عكس دوال متعددات الحدود التي قابلناها سابقا فإن الدوال النسبية عادة ما تكون غير مُعرفة لجميع قيّم المتغيرات. إذا نظرنا على سبيل المثال إلى الدلة النسبية أعلاه فإن المقام \(x-1\) لا يأخذ القيمة صفر وذلك لأن القسمة على صفر غير مُعرفة.
وهذا ما يقودنا إلى مفهومي المجال والمدى.
مجال الدالة هو القيّم التي يمكن أن يأخذها المتغير المستقل المدرج في تعبير الدالة. في المثال أعلاه المتغير هو \(x\). بما أن \(x-1\) يجب ألا تساوي صفر فهذا يعني أن \(x\) يجب ألا تساوي 1. بالتالي فإن مجال هذه الدالة هو جميع الأعداد الحقيقية ما عدا الواحد الصحيح.
مدى الدالة هو القيّم التي يمكن أن تأخذها الدالة. بمعنى آخر المدى هو قيّم الدالة التي يمكننا الحصول عليها بتعويض قيّم المتغير المستقل في تعبير الدالة. غالباً ما يكون رسم الدالة بيانيا من أسهل الطُريق للحصول على فكرة عامة عن مدى الدالة. يجب الإنتباه إلى كيفية تغيرات قيّم الدالة خاصة عندما تقترب قيمة المتغير المستقل إلى عدد غير مُعرّف (أي خارج نطاق مجال الدالة).
بما أن هنالك دوال نسبية قد تكون غير مُعرفة لجميع قيم المتغيرات فغالبا ما يكون رسمها البياني متقطع أو غير متصل. فيما يلي مثال على شكل بياني لمثل هذا النوع من الدوال النسبية.
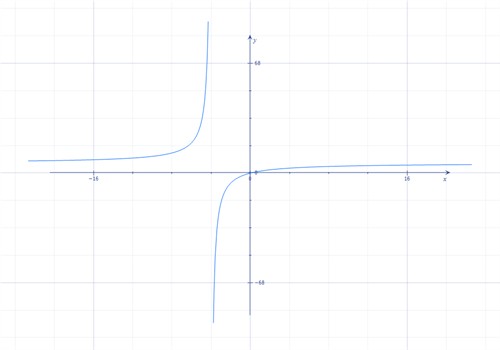
هذا النوع من المنحنيات غالبا ما يتكرر عندما نتعامل مع الدوال النسبية.
نلاحظ أن منحنى هذه الدالة يقترب من محور \(x\) عند قيّم المتغير \(x\) السالبة الكبيرة ولكن عندما تقترب قيمة المتغير \(x\) من \(-4\) \((x=-4)\) تزداد قيمة الدالة بشكل حاد ويرتفع المنحنى أكثر فأكثر في اتجاه \(y\) الموجب اللانهائي وكلما اقتربت قيمة \(x\) أكثر فأكثر من \(x=-4\). حيث أن المنحنى غير مستمر فإن اتجاههه سيتغير فجأة عندما تزيد قيّمة المتغير \(x\) وتصبح أكبر من \(-4\) ويكون المنحنى في اتجاه \(y\) السالب اللانهائي ومن ثم يستقر المنحنى بالقرب من محور \(x\) عندما تصبح قيّم \(x\) أكبر فأكبر من \(-4\).
في القسم القادم سندرس هذا النوع من الدوال بصورة أكثر تفصيلاً.
فيديو الدرس
ما هي قيّم \(x\) المُعرفه عندها الدالة (أي أوجد مجال الدالة).
