نسبة التغيٌّر

في أغلب الأحيان يهتم الكثير منا بمعرفة كيفية تَغَيُر القيّم خلال فترة زمنية معينة. قد يكون على سبيل المثال تغيُر درجة حرارة تيرموس الشاي/القهوة خلال 5 ساعات، أو زيادة أو نقصان عدد السكان على مدار 10 سنوات كمثال آخر. كيف يمكننا معرفة مثل هذه التغيُرات؟

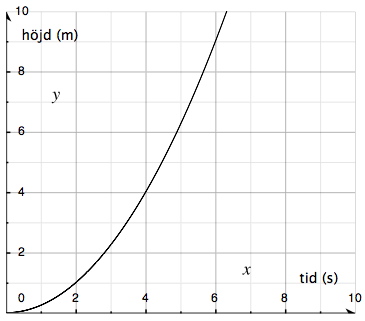
في الشكل التالي لدينا منحنى يوضح كيفية تحرك شيء ما مرتفعا الى الأعلى.

معاني الكلمات على الرسم:

اللغة العربية	اللغة السويدية
الإرتفاع (متر)	\((m)\) höjd
الزمن (ثانية)	\((s)\) tid

 

 

يمكننا من الشكل مباشرة قراءة ارتفاع هذا الشئ في زمن معين على سبيل المثال, أو يمكننا قرآءة الزمن (بالثواني) الذي استغرقه هذا الشيء في الوصول إلى ارتفاع معين.

ولكن ما هو متوسط معدّل الزيادة في الارتفاع في الفترة الزمنية ما بين 2 إلى 6 ثواني على سبيل المثال؟ من الشكل يمكننا قراءة أن الارتفاع كان 1 متر عندما كان الزمن 2 ثانية ثم إزداد وأصبح 9 أمتار عندما كان الزمن 6 ثواني. التغيُر في الإرتفاع (8 أمتار) يُمثل تغيُر \(y\) والتغيُر في الزمن (4 ثواني) هو التغيُر في \(x\).

في الشكل أدناه نلاحظ نقطتي التغيُر \((2, 1)\) و \((6, 9)\) المحددتين على المنحنى. كما يمكننا أيضا ملاحظة التغيُر في \(x\) والتغيُر في \(y\) بين هاتين النقطتين على المنحنى. تم رسم خط مستقيم أزرق بين هاتين النقطتين على المنحنى. هذا النوع من الخطوط المستقيمة والذي يقطع المنحنى عند نقطتين على الأقل يُسمى بالمستقيم القاطع.

 

 

 

 

 

 

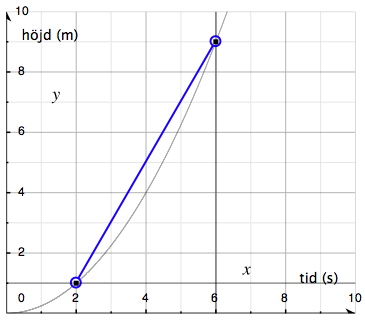
متوسط معدل الزيادة في الارتفاع خلال الفترة الزمنية ما بين 2 ثانية إلى 6 ثواني يمكننا الحصول عليه بقسمة الفرق في الارتفاع على الفرق في الزمن:

$$\frac{y_2-y_1}{x_2-x_1}=\frac{9-1}{6-2}=\frac{8}{4}=2  \frac{m}{s}$$

لاحظ أن هذه الصيغة هي نفس الصيغة التي استخدمناها عندما قمنا بحساب معامل ميل الخط المستقيم (k) باستخدام نقطتين معلومتين. بحساب ميل المستقيم القاطع يمكننا إيجاد متوسط معدل التغيُر في مدى مُعين (بين هاتين النقطتين).

متوسط معدل التغيّر هذا يُسمى أيضا بنسبة التغيّر وهو يُمثل متوسط ميل المنحنى في مدى معين.

فيديو الدرس

مفهوم نسبة التغيُر ومثال على ذلك.